[Python] 주성분 분석(Principle Component Analysis, PCA)과 특이값 분해(Singular Value Decomposition, SVD)

주성분 분석(Principle Component Analysis, PCA)

주성분 분석(Principle Component Analysis, PCA)이란 차원 축소 알고리즘 중 하나이다. 일반적으로 머신러닝을 이용해 문제 해결을 시도할 때 train sample은 보통 수천 또는 수백만 개의 특성(feature)을 가지고 있다. 이렇게 특성들이 많으면 이 중 어떤 특성이 유의미한 요소인지 찾기 힘들고 동시에 많은 불필요한 데이터로 인해 garbage in garbage out을 경험하게 된다. 뿐만 아니라 학습 시간이 길어져 결국 연구 결과 확인까지 오래 걸릴 수 있다. 따라서 이런 문제를 야기하는 것을 차원의 저주(curse of dimensionality)라고 한다. 다시 말해 결국 차원을 축소하면 이 문제를 해결할 수 있다. 이에 PCA를 적용해보고자 한다.

 

하지만 PCA를 사용하기 전 짚고 넘어가야 할 것이 있다. PCA는 단순히 주성분 분석이라기보다는 주성분이 될 수 있는 형태로 내가 가지고 있는 기존 데이터에 어떤 변환을 가하는 것이다. 즉, 당연히 원본 데이터는 어떠한 기준에 의해 변환이 생기게 되고 그 변환을 통해 주성분을 추출한다. 따라서 이 PCA를 통해 도출된 데이터는 원본 데이터와 다른 변환된 데이터이므로 원래 변수가 가지고 있는 의미 즉 열의 의미가 중요한 경우에는 PCA를 사용하면 안 된다.

 

위에서 언급하였 듯 PCA는 데이터 하나하나에 대한 성분을 분석하는 것이 아니라, 여러 데이터들이 모여 하나의 분포를 이룰 때 이 분포의 주 성분을 분석해 주는 방법이다. 여기서 주성분이라 함은 그 방향으로 데이터들의 분산이 가장 큰 방향벡터를 의미한다.

 

Fig 1. 2차원에서의 PCA

 

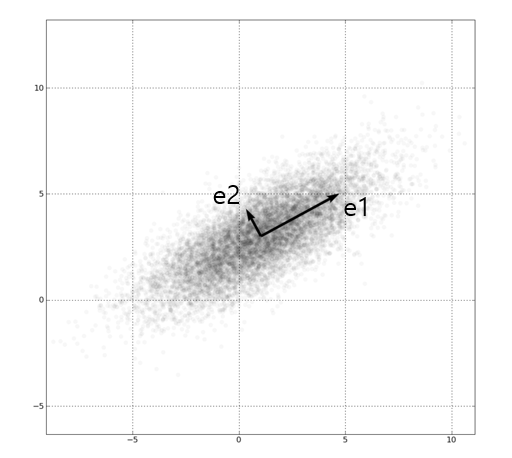
우선 위 그림에서 첫 번째 PCA 축을 e1, 두 번째 PCA 축을 e2라고 가정한다. e1 방향을 따라 데이터들의 분산(흩어진 정도)이 가장 크다. 그리고 e1에 수직이면서 그다음으로 데이터들의 분산이 가장 큰 방향은 e2이다. PCA는 2차원 데이터 집합에 대해 PCA를 수행하면 2개의 서로 수직인 주성분 벡터를 반환하고, 3차원 점들에 대해 PCA를 수행하면 3개의 서로 수직인 주성분 벡터들을 반환한다. 3차원 데이터의 경우 아래 그림과 같이 3개의 서로 수직인 주성분 벡터를 찾아준다.

 

Fig 2. 3차원에서의 PCA

 

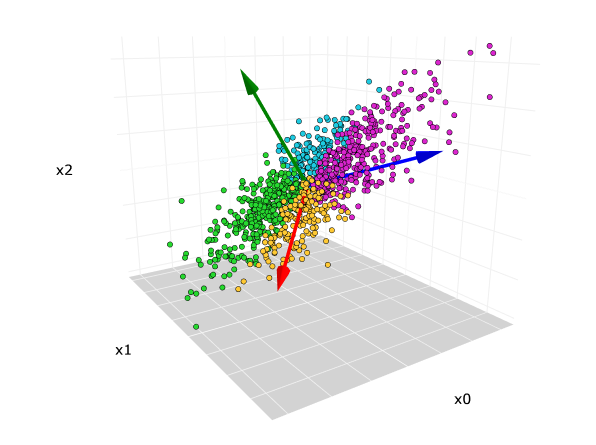
만약 저차원의 초평면에 투영을 하게 된다면 차원은 줄어들게 된다. 그럼 어떤 초평면이 가장 최적인가에 대해 정의해야 한다. 아래 그림을 토대로 생각해 볼 수 있다.

 

Fig 3. 초평면 투영

 

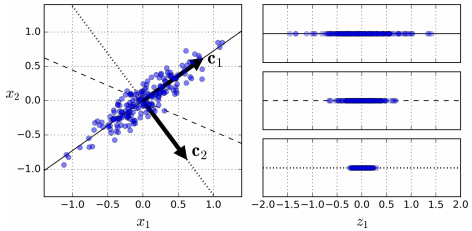
우측 그래프에서 볼 수 있듯 c1은 분산을 가장 크게 보존하고, c2가 가장 분산을 적게 만드는 선이다. 초평면을 다른 방향으로 투영하는 것보다 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있다고 생각할 수 있다. 분산이 커야 데이터들 사이의 차이점이 명확해지고, 이를 통해 우리의 모델을 더욱 좋은 방향으로 만들 수 있기 때문이다. 즉, PCA는 분산을 보존하는 것이 중요하다.

 

Fig 4. 초평면과 분산

 

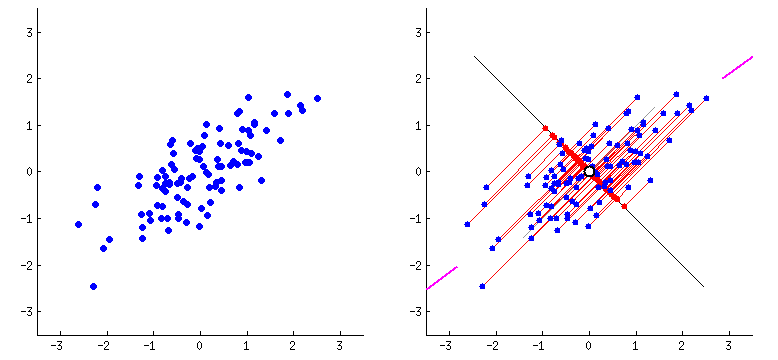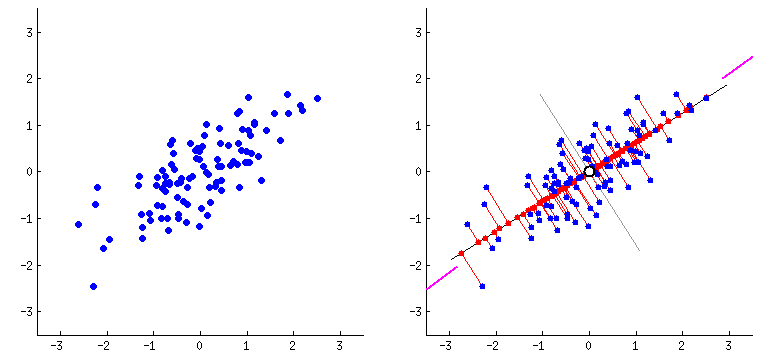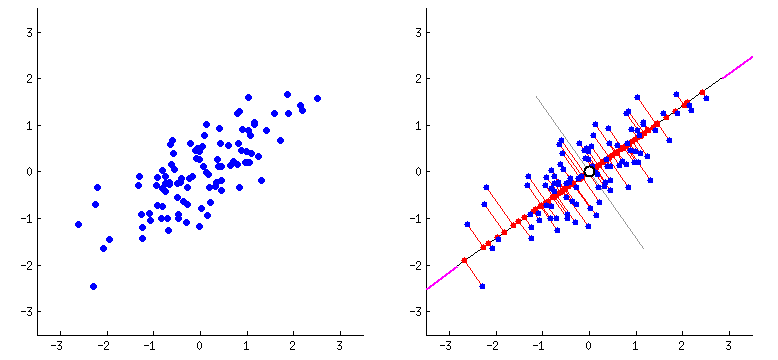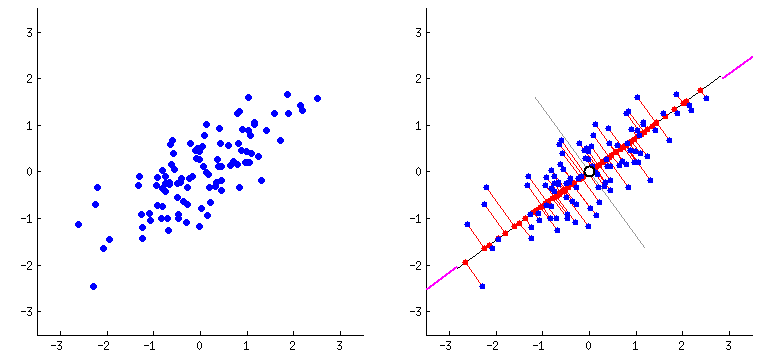
위 그림에서 알 수 있듯 분산이 최대인 축에서 데이터와 초평면간의 거리는 최소가 된다.

 

특이값 분해(Singular Value Decomposition, SVD)

주성분을 찾기위해 수행하는 특이값 분해(Singular Value Decomposition, SVD)는 임의의 \(m*n\) 행렬을 분해할 수 있는 행렬 분해(decomposition) 방법 중 하나이다. 즉, 직교하는 벡터 집합에 대해 선형 변환 후 그 크기가 변해도 여전히 직교할 수 있게 되는 직교 집합은 무엇인지, 그리고 선형 변환 후의 결과가 무엇인지에 대한 해답을 찾기 위해 사용된다. 수식은 아래와 같다.

$$ A = U⋅\Sigma{V^T} $$

• \( A: m * n \) rectangular matrix
• \( U: m * m \) orthogonal matrix
• \( \Sigma: m * n \) diagonal matrix
• \( V: n * n \) orthogonal matrix

 

해당 수식에서 우리가 필요한 모든 주성분은 V에 담겨있다.

 

PC(Principle Component)를 추출했다면 처음 d개의 주성분으로 정의한 초평면에 투영하여 데이터셋의 차원을 d차원으로 축소할 수 있다. 이 초평면은 분산을 가능한 최대로 보존한 투영이다. 초평면에 훈련 세트를 투영하기 위해서는 행렬 \( X \)와 첫 d개의 주성분을 담은 \( V \)의 첫 d열로 구성된 행렬인 \( W_d \)를 dot product하면 된다.

$$ X_{d-proj} = X⋅W_d $$

 

python을 이용해 PC를 추출하기 위해 Numpy와 sklearn을 사용할 수 있다. 아래는 두 방법으로 가장 주요한 2개의 PC를 추출하는 소스 코드이다. 우선은 임의의 데이터 셋 X가 있다고 가정한다.

 

Numpy

import numpy as np

# svd
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]

# 투영
W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)

 

sklearn

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X2D = pca.fit_transform(X)

 

실험

아래는 실제 데이터를 이용한 실습이다. 우선 데이터를 load한 후 정규화를 진행한다. 단, target 정보(꽃 종류)는 정규화를 진행하지 않았다.

 

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import numpy as np
import pandas as pd


# 데이터셋 로드
iris = load_iris()
df = pd.DataFrame(data=np.c_[iris.data])

# 데이터셋 정규화
scaler = StandardScaler()
scaler.fit(df)
df_scaled = scaler.transform(df)

# type casting with setting target
df_scaled = pd.DataFrame(df_scaled, columns=['sepal length', 'sepal width', 'petal length', 'petal width'])
df_scaled['target'] = iris.target

print(df_scaled)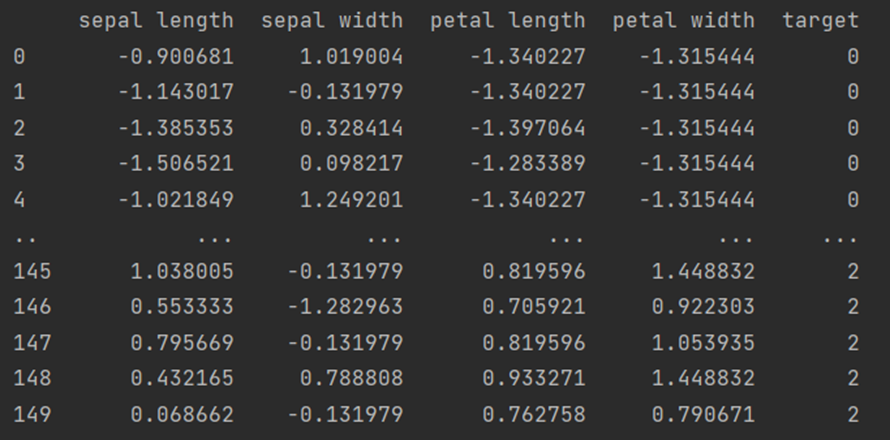

Fig 5. 정규화 결과

 

4가지 feature가 평균 0, 표준 편차 1을 기준으로 정규화된 결과를 볼 수 있다. 다음으로 이 정규화된 데이터를 2개의 주성분으로 차원 축소한다. 다만, target class 정보가 feature에 포함되지 않도록 주의해야 한다. 또한 원본 데이터에 대해 이 축소된 결과의 설명력을 알 수 있다.

 

from sklearn.decomposition import PCA

# 2차원으로 차원 축소, target 정보는 제외
pca = PCA(n_components=2)
pca.fit(df_scaled.iloc[:, :-1])

# 데이터 프레임으로 자료형 변환 및 target class 정보 추가
df_pca = pca.transform(df_scaled.iloc[:, :-1])
df_pca = pd.DataFrame(df_pca, columns=['component 0', 'component 1'])

print(df_pca)
print(pca.explained_variance_ratio_)	# [0.72962445 0.22850762]

Fig 6. PCA 수행 후 차원 축소 결과

 

차원 축소된 결과에서 첫 주성분이 가장 데이터 분포에서의 분산에 대한 설명력이 높고 이후 주성분으로 갈수록 설명력이 점차 낮아지게 된다. 위에서 학습된 PCA 모듈의 explained_variance_ratio_에서 각 주성분에 대한 설명력을 확인할 수 있다. 일반적으로 데이터 차원의 수가 큰 경우 총 주성분 설명력 비율의 합이 80~90%를 넘는 정도가 되는 선까지의 정보를 활용한다. 위의 예시에서는 첫 주성분이 대략 73%, 두 번째 주성분이 대략 23%의 분산 설명력을 가져 두 주성분이 4차원의 데이터 분포의 특징 중 약 96%를 설명하고 있다.

 

아래는 분포 시각화이다.

 

import matplotlib.pyplot as plt

# class target 정보 불러오기
df_pca['target'] = df_scaled['target']

# target 별 분리
df_pca_0 = df_pca[df_pca['target'] == 0]
df_pca_1 = df_pca[df_pca['target'] == 1]
df_pca_2 = df_pca[df_pca['target'] == 2]

# target 별 시각화
plt.scatter(df_pca_0['component 0'], df_pca_0['component 1'], color='orange', alpha=0.7, label='setosa')
plt.scatter(df_pca_1['component 0'], df_pca_1['component 1'], color='red', alpha=0.7, label='versicolor')
plt.scatter(df_pca_2['component 0'], df_pca_2['component 1'], color='green', alpha=0.7, label='virginica')

plt.xlabel('component 0')
plt.ylabel('component 1')
plt.legend()
plt.show()

Fig 7. 시각화

 

완벽하게 분리해내지는 못했지만 두 주성분이 꽃 종류별 feature들의 분포 특징을 나름 잘 잡아내고 있는 것을 확인할 수 있다.

이제 마지막으로 PCA가 정말 회귀분석 등 모델을 만들 때 도움이 되는지 확인해본다. PCA를 이용해 feature를 각 4개, 2개로 산출하고 이 산출된 데이터를 LogisticRegression에 대입하여 실험을 진행하였다.

 

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix


def pca_test(n=2):
    X = iris.data
    y = iris.target

    # 2차원으로 차원 축소, target 정보는 제외
    pca = PCA(n_components=n)
    pca.fit(X)

    # 데이터 프레임으로 자료형 변환 및 target class 정보 추가
    df_pca = pca.transform(X)

    clf = LogisticRegression(max_iter=1000, random_state=0, multi_class='multinomial')

    # origin
    if X.shape[1] > n:
        X = X[:, :n]
    clf.fit(X, y)
    pred = clf.predict(X)
    print(confusion_matrix(y, pred))

    # pca
    clf.fit(df_pca, y)
    pred = clf.predict(df_pca)
    print(confusion_matrix(y, pred))
    

pca_test(n=4)
# origin
# [[50  0  0]
#  [ 0 47  3]
#  [ 0  1 49]]
# pca
# [[50  0  0]
#  [ 0 47  3]
#  [ 0  1 49]]

pca_test(n=2)
# origin
# [[50  0  0]
#  [ 0 37 13]
#  [ 0 14 36]]
# pca
# [[50  0  0]
#  [ 0 47  3]
#  [ 0  2 48]]

 

혼동 행렬을 통해 결과를 확인할 수 있다. 먼저 feature가 4개 일 때는 원본 데이터의 feature도 4개로 동일하고 이 경우 크게 차이가 없다. 하지만 feature의 개수가 2개로 줄었을 때는 좀 더 확연한 차이가 나는 것을 볼 수 있다. 물론 원본 데이터도 무작위로 2개의 feature만 추출하였다.

 

def pca_test(n=2):
    X = iris.data
    y = iris.target

    # 2차원으로 차원 축소, target 정보는 제외
    pca = PCA(n_components=n)
    pca.fit(X)

    # 데이터 프레임으로 자료형 변환 및 target class 정보 추가
    df_pca = pca.transform(X)

    clf = LogisticRegression(max_iter=1000, random_state=0, multi_class='multinomial')

    # origin
    clf.fit(X, y)
    pred = clf.predict(X)
    print(confusion_matrix(y, pred))

    # pca
    clf.fit(df_pca, y)
    pred = clf.predict(df_pca)
    print(confusion_matrix(y, pred))

pca_test(n=2)
# origin
#[[50  0  0]
# [ 0 47  3]
# [ 0  1 49]]
# pca
#[[50  0  0]
# [ 0 47  3]
# [ 0  2 48]]

 

위의 결과는 PCA를 이용해 2개의 feature를 도출하고 원본은 4개의 feature를 모두 사용한 실험 결과인데 두 결과값이 크게 차이 나지는 않았다.

 

아래는 전체 python 소스 코드이다.

 

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 데이터셋 로드
iris = load_iris()
df = pd.DataFrame(data=np.c_[iris.data])


def normalize(df):
    # 데이터셋 정규화
    scaler = StandardScaler()
    scaler.fit(df)
    df_scaled = scaler.transform(df)

    # type casting with setting target
    df_scaled = pd.DataFrame(df_scaled, columns=['sepal length', 'sepal width', 'petal length', 'petal width'])
    df_scaled['target'] = iris.target

    print(df_scaled)

    return df_scaled


def draw_plot(df_scaled):
    # 2차원으로 차원 축소, target 정보는 제외
    pca = PCA(n_components=2)
    pca.fit(df_scaled.iloc[:, :-1])

    # 데이터 프레임으로 자료형 변환 및 target class 정보 추가
    df_pca = pca.transform(df_scaled.iloc[:, :-1])
    print(df_pca)
    print(pca.explained_variance_ratio_)

    df_pca = pd.DataFrame(df_pca, columns=['component 0', 'component 1'])

    # class target 정보 불러오기
    df_pca['target'] = df_scaled['target']

    # target 별 분리
    df_pca_0 = df_pca[df_pca['target'] == 0]
    df_pca_1 = df_pca[df_pca['target'] == 1]
    df_pca_2 = df_pca[df_pca['target'] == 2]

    # target 별 시각화
    plt.scatter(df_pca_0['component 0'], df_pca_0['component 1'], color='orange', alpha=0.7, label='setosa')
    plt.scatter(df_pca_1['component 0'], df_pca_1['component 1'], color='red', alpha=0.7, label='versicolor')
    plt.scatter(df_pca_2['component 0'], df_pca_2['component 1'], color='green', alpha=0.7, label='virginica')

    plt.xlabel('component 0')
    plt.ylabel('component 1')
    plt.legend()
    plt.show()


def pca_test(n=2):
    X = iris.data
    y = iris.target

    # 2차원으로 차원 축소, target 정보는 제외
    pca = PCA(n_components=n)
    pca.fit(X)

    # 데이터 프레임으로 자료형 변환 및 target class 정보 추가
    df_pca = pca.transform(X)

    clf = LogisticRegression(max_iter=1000, random_state=0, multi_class='multinomial')

    # origin
    if X.shape[1] > n:
        X = X[:, :n]
    clf.fit(X, y)
    pred = clf.predict(X)
    print(confusion_matrix(y, pred))

    # pca
    clf.fit(df_pca, y)
    pred = clf.predict(df_pca)
    print(confusion_matrix(y, pred))


draw_plot(normalize(df))
pca_test(n=4)
pca_test(n=2)

 

응용

PCA는 조금 다른 방법이지만 face recognition에서도 응용될 수 있다. 인식 대상이 되는 사람들의 얼굴 샘플들만 모아 이 샘플들에 대한 PCA를 k개의 주요 eigenface들을 구한 후 각 개인들을 eigenface로 근사했을 때의 근사 계수를 저장한다. 즉, \( x_k = c_1e_1 + ... + c_ke_k \)일 때 \( (c_1, ..., c_k) \)를 개인의 고유 feature로 저장한다. 이후 입력 데이터 x가 들어왔을 때 이를 k개의 eigenface로 근사한 근사 계수가 미리 저장된 개인별 근사 계수들 중 누구와 가장 가까운지를 조사하여 x를 식별할 수 있다. 이와 비슷하게 PCA를 이용하여 얼굴영상에서 안경 쓴 사람의 안경 영역을 찾아서 안경이 제거된 얼굴 영상을 얻을 수 있는 방법도 있다고 한다.

 

관련 포스트

2021.12.28 - [Data Science/Statistics] - [Python] VIF(Variance Inflation Factors)를 이용한 다중공선성(Multicollinearity) 판단

 

---

참고 자료

 

https://ko.wikipedia.org/wiki/%EC%A3%BC%EC%84%B1%EB%B6%84_%EB%B6%84%EC%84%9D

 

https://towardsdatascience.com/principal-component-analysis-pca-explained-visually-with-zero-math-1cbf392b9e7d

 

https://laptrinhx.com/dimensionality-reduction-principal-component-analysis-359354885/

 

https://butter-shower.tistory.com/210

 

https://darkpgmr.tistory.com/110

 

https://m.blog.naver.com/tjdrud1323/221720259834

 

https://jimmy-ai.tistory.com/128

 

https://chancoding.tistory.com/53

 

https://angeloyeo.github.io/2019/08/01/SVD.html

 

소스 코드

 

https://github.com/sehoon787/Personal_myBlog/blob/main/Data%20Science/Statistics/blog_statistics_31.py