주요 개념
- 다항 회귀(Polynomial Regression)
- 비선형 데이터
- 편향(Bias)
- 분산(Variance)
다항 회귀(Polynomial Regression)란 비선형 데이터를 학습하기 위해 선형 모델을 사용하는 기법이다. 단순 선형 회귀(SLR)를 이용해 모든 데이터의 관계성을 직선으로 표현할 수는 없으므로 다항 회귀 또는 다중 선형 회귀(MLR) 등과 같은 조금 더 복잡한 회귀 모델이 때에 따라 최적의 회귀선을 나타내고는 한다. 각 변수의 거듭제곱을 새로운 변수로 추가하고 이 확장된 변수를 포함한 데이터셋에 선형 모델을 훈련시킨다.
다중 선형 회귀는 여러 독립 변수들이 필요한 반면 다항 회귀는 하나의 독립 변수에 대한 차수를 확장해가며 단항식이 아닌 2차, 3차 등의 회귀 모델을 도출한다. 다만 주의해야 할 점은 선형 회귀와 비선형 회귀를 구분하는 것은 "독립변수"의 선형성이 아니라, "회귀 계수"의 선형성이라는 것이다. 아래는 다항 회귀 모델로 산출되는 수식이다.
$$ f(x)=w_{n}x^n+w_{n-1}x^{n-1}+...+w_2x^2+w_1x+b $$
직선으로 어떤 데이터를 충분히 표현하지 못하는 경우를 편향(bias)이 크다고 한다. 지나치게 한 방향으로 치우쳐져 있기 때문이다.
반대로 다항 회귀에서는 차수가 너무 큰 경우에는 변동성이 커지고, 이를 고분산성을 가진다고 한다.
편향(Bias)과 분산(Variance)은 한쪽의 성능을 좋게 하면, 나머지 하나의 성능이 떨어지는 trade-off 관계에 있다. 쉽게 말해 편향을 줄이면 분산이 늘어나고, 분산을 줄이면 편향이 늘어나게 된다.
이 둘의 성능을 적절하게 맞춰 전체 오류가 가장 낮아지는 지점을 골디락스 지점이라고 한다. 이 지점을 찾는 것이 모든 회귀식과 관련된 분석에서 가장 중요하다.
다음은 python을 이용한 다항 회귀의 구현이다. 다항 회귀는 sklearn의 선형 회귀 함수에 독립 변수를 다항식으로 변환하여 삽입하면 되므로 따로 직접 구현하는 과정은 생략한다. 회귀식을 직접 구현하는 과정은 여기를 참조하면 된다.
우선 데이터 생성이다.
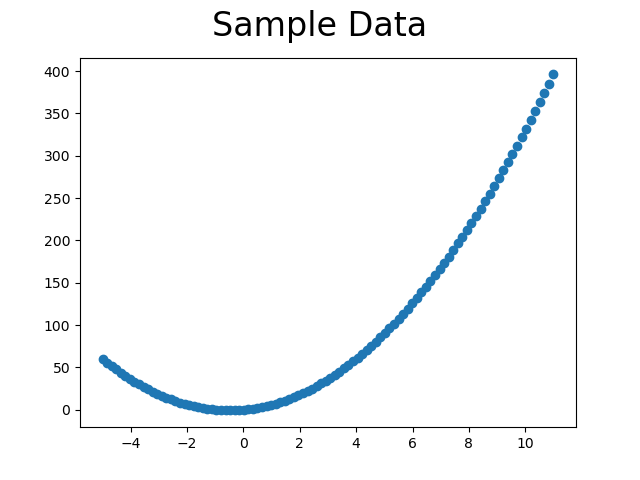
import matplotlib.pyplot as plt
import numpy as np
def make_data(size=100, noise=1):
x = np.linspace(-5, 11, size).reshape(-1, 1)
y = 3*x**2 + 3*x
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
plt.scatter(x, y)
plt.suptitle("Sample Data", size=24)
plt.show()
return x, yy
아래는 다항 회귀 도출을 위해 독립 변수 x에 PolynomialFeatures 함수를 적용하는 부분이다. interection_only=True로 지정하면 거듭제곱이 포항된 항은 제외된다. 즉, 1차 항과 상수항만 남게 되는 것이다. 또한 다항 회귀의 차수(degree)가 높아질수록 더 훈련데이터에 fitting을 시도하는데 이때 overfitting의 위험이 있다. 이는 특성의 개수가 과도하게 많아졌기 때문인데 이는 sklearn의 릿지(Ridge, L2 규제), 라쏘(Lasso, L1 규제) 클래스를 이용해 규제를 둠으로써 해결할 수 있다.
먼저 릿지(Ridge)는 변형된 데이터 변수를 모두 사용하지만 계수는 줄이는 방식으로 규제(Regulation)를 둔다.
다음으로 라쏘(Lasso)는 일정 변수들의 계수를 0으로 만들어 사용하지 않도록 하는 방법을 이용한다. 따라서, 라쏘를 사용하면 데이터가 손실되어 정확도가 떨어지는 위험성이 있기도 하다.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import r2_score
def poly(x, degree=2):
model = PolynomialFeatures(degree=degree, include_bias=False)
x_poly = model.fit_transform(x)
return x, x_poly
주어진 데이터를 다항 회귀와 단순 선형 회귀를 이용해 각각 표현해보면 아래와 같다.
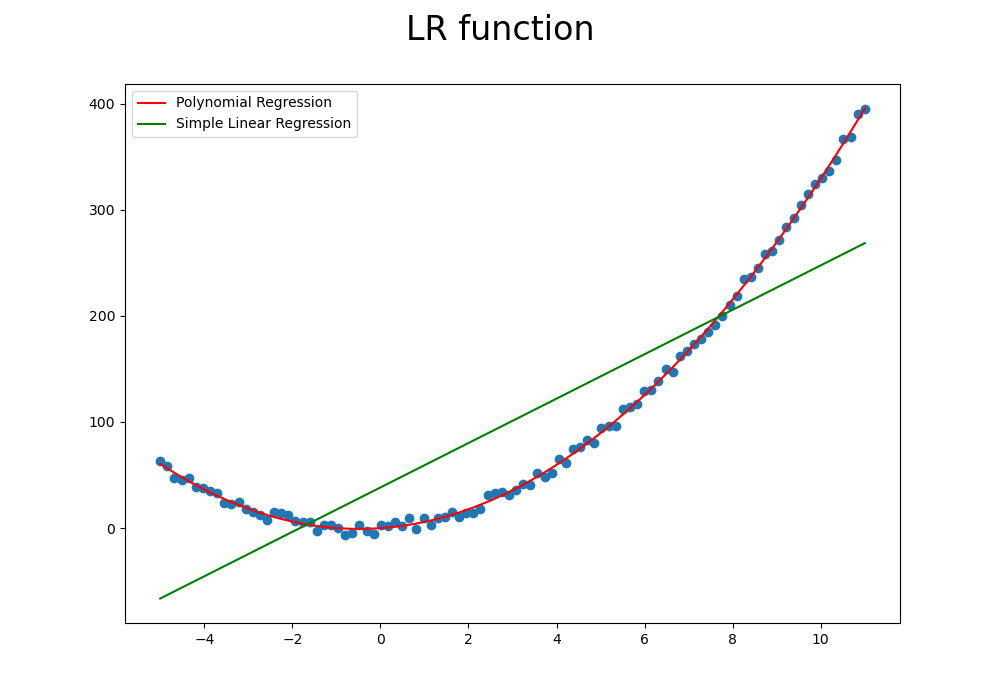
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
def LR(poly_x, x, y):
SLR_model = LinearRegression()
model = LinearRegression()
SLR_model.fit(x, y)
model.fit(poly_x, y)
print("w1: ", model.coef_[0][0])
print("w2: ", model.coef_[0][1])
print("b: ", model.intercept_[0])
SLR_result = SLR_model.predict(x)
result = model.predict(poly_x)
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.plot(x, result, color='red', label='Polynomial Regression')
plt.plot(x, SLR_result, color='green', label='Simple Linear Regression')
plt.suptitle("LR function", size=24)
plt.legend()
plt.show()
return result
x, y = make_data(size=100, noise=6)
x, x_poly = poly(x)
result = LR(x_poly, x, y)
data = np.concatenate((x, y, result), axis=1)
df = pd.DataFrame(data, columns=['x', 'y', 'predict'])
print("결정계수: ", r2_score(y, result))
print("상관계수: \n", df.corr())
print("MSE: ", mean_squared_error(y, result))
# w1: 3.088145089337895
# w2: 2.991563564168224
# b: 0.6733335620988612
# 결정계수: 0.999178861266219
# 상관계수:
# x y predict
# x 1.000000 0.859681 0.860034
# y 0.859681 1.000000 0.999589
# predict 0.860034 0.999589 1.000000
# MSE: 10.702276737672278
선형 회귀보다 다항 회귀가 저런 곡선 구간이 존재하는 데이터의 특징을 더 잘 설명하고 있다. 여기서 산출되는 가중치는 coef_[0][0]번부터 1차 항의 가중치로 순차적 적용을 하면 된다. 예를 들어 위 수식에서 w1=3.08, w2=2.99, b=0.67인데 \( w_1*x +w_2*(x^2)+b \)로 표현된다.
이번에는 차수를 100차로 올려보았다.
따로 수치로 확인하지 않아도 2차를 적용했을 때보다 좋지 않다는 것이 보인다. Ridge, Lasso나 데이터 전처리 등을 이용해 데이터를 잘 정제해가며 파라미터들을 잘 조정하면 더 좋은 결과가 나올 것이다.
아래는 전체 python 소스 코드이다.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import r2_score
def make_data(size=100, noise=1):
x = np.linspace(-5, 11, size).reshape(-1, 1)
y = 3*x**2 + 3*x
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
plt.scatter(x, y)
plt.suptitle("Sample Data", size=24)
plt.show()
return x, yy
def poly(x, degree=2):
model = PolynomialFeatures(degree=degree, include_bias=False)
x_poly = model.fit_transform(x)
return x, x_poly
def LR(poly_x, x, y):
SLR_model = LinearRegression()
model = LinearRegression()
SLR_model.fit(x, y)
model.fit(poly_x, y)
print("w1: ", model.coef_[0][0])
print("w2: ", model.coef_[0][1])
print("b: ", model.intercept_[0])
SLR_result = SLR_model.predict(x)
result = model.predict(poly_x)
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.plot(x, result, color='red', label='Polynomial Regression')
plt.plot(x, SLR_result, color='green', label='Simple Linear Regression')
plt.suptitle("LR function", size=24)
plt.legend()
plt.show()
return result
x, y = make_data(size=100, noise=6)
x, x_poly = poly(x)
result = LR(x_poly, x, y)
data = np.concatenate((x, y, result), axis=1)
df = pd.DataFrame(data, columns=['x', 'y', 'predict'])
print("결정계수: ", r2_score(y, result))
print("상관계수: \n", df.corr())
print("MSE: ", mean_squared_error(y, result))
관련 포스트
2022.02.15 - [Data Science/Statistics] - [Python] 결정계수 R2 score(R-squared)와 조정된 결정계수(Adjusted R-squared)의 이해
2022.02.23 - [Data Science/Statistics] - [Python] 단순 선형 회귀(Simple Linear Regression, SLR)의 이해와 구현
2022.02.24 - [Data Science/Statistics] - [Python] 다중 선형 회귀(Multiple Linear Regression, MLR)의 이해와 구현
2022.02.24 - [Data Science/Statistics] - [Python] 다중 선형 회귀(Multiple Linear Regression, MLR)의 이해와 구현
참고 자료
https://dsbook.tistory.com/192
https://bioinformaticsandme.tistory.com/290
https://kimdingko-world.tistory.com/236
https://itstory1592.tistory.com/7
소스 코드
