주요 개념
- 분류 알고리즘
- 로지스틱 회귀(Logistic Regression)
- 비용 함수 or 손실 함수(Cost Function or Loss Function)
- 이진 교차 엔트로피(Binary Cross Entropy)
- 경사 하강법(Gradient Descent)
- 지역 최소(Local Minimum)
로지스틱 회귀(Logistic Regression)

로지스틱 회귀(Logistic Regression)는 범주형 변수를 예측하기 위해 설계된 알고리즘으로 선형 회귀 모델을 변형하여 확률 기반의 예측을 수행한다. 주로 이진 분류(binary classification) 문제에 사용되지만 다중 범주형 변수도 예측할 수 있다.
예를 들어 "합격/불합격", "스팸/비스팸", "긍정/부정"과 같은 이진 분류 문제 외에도 다중 클래스 문제에서 여러 범주를 예측하는 데 활용할 수 있다.
다시 말해, 분석하고자 하는 대상(특징)이 2개 또는 그 이상의 집단으로 나누어져 있을 때, 개별 관측치들이 어느 집단에 분류될 수 있는지에 대해 분석하고 예측하는 모델을 개발하는 통계적 기법이다. 이름만 회귀이지 사실 분류 알고리즘이다.
예를 들어 독립 변수인 혈압은 숫자 그 자체로 의미를 지니는 변수이지만, 암 발생 여부는 그렇다 아니다와 같이 이분법으로 나누게 된다. 발병(1)과 정상(0) 사이에 중간 범주가 없을뿐더러 심지어 정상을 1, 발병을 0으로 바꾸어도 큰 상관이 없다. 종속변수의 숫자는 큰 의미를 가지지 않는다는 뜻이다.
따라서 회귀식의 결과값이 0, 1로만 도출될 때, 이에 근사하는 직선 혹은 모델을 만드는 것이 힘들다. 이러한 베르누이 분포를 따르는 이진 데이터를 분류할 때 가장 많이 활용되는 것이 로지스틱 회귀이다. 물론 다중 클래스 분류 문제로도 확장은 가능하다.
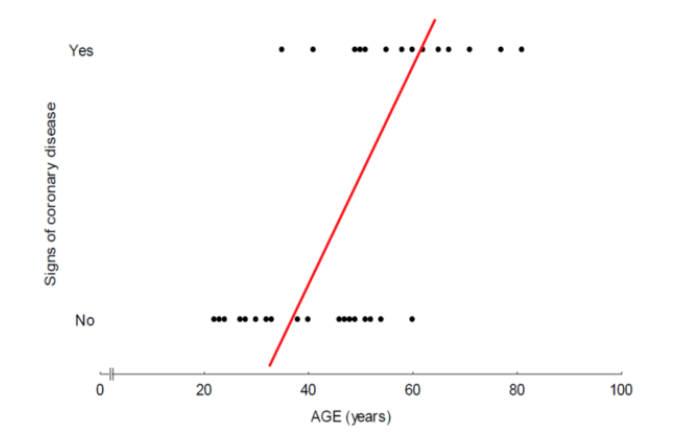
위와 같은 문제점을 해결하기 위해 종속 변수를 확률 변수로 치환하는 방법을 적용한다. 이를 통해 (0, 1)을 0≤P(Y=1│X)≤1로 나타낼 수 있다. 하지만 이 역시 p(x)= \( wx+b \)의 모델은 회귀선에 의해 음수값을 추정하거나, 경우에 따라 1을 초과하는 추정값이 발생할 수도 있다.
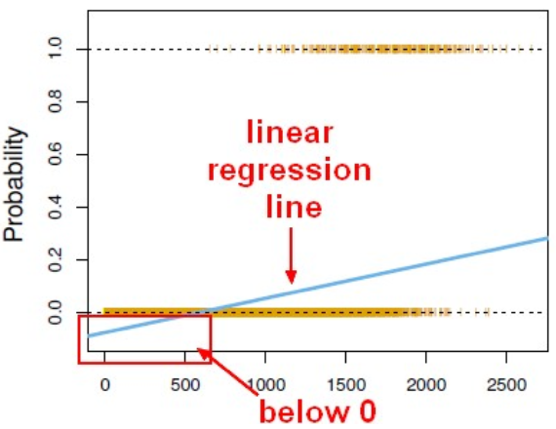
이는 확률값 P를 -∞부터 ∞까지 확장하여 해결할 수 있고, 따라서 임의의 사건이 발생하지 않을 확률 대비 일어날 확률의 비율을 뜻하는 오즈(Odds)를 이용한다. 오즈는 직역하면 가능성이다.
$$ p(x)=wx+b $$
$$ odds=\frac{p(x)}{1-p(x)} $$
이를 통해 계산되는 y의 결과값은 [0, ∞]이다. 여기에 로그를 취하여 로짓(logit) 변환을 수행한다.
$$ logit(p)=log(odds)=z $$
이 과정들을 수행하면 최종적으로 아래와 같은 로지스틱 회귀 가설이 완성된다.
$$ logitstic(z)=μ(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(wx+b)}} $$
이렇게 범위가 무한한 입력값들을 시그모이드(로지스틱) 함수를 이용해 결과값을 [0,1]의 범위로 압축하였다.
이런 형태의 이항 분류(binary classification)에 적절한 함수로 시그모이드(sigmoid) 함수가 있다. 그래프의 모양은 S자 형태로 중심축 (x=0)을 중심으로 좌측은 0으로 수렴하고 우측은 1로 수렴한다.

이제 z값은 사건이 발생할 확률을 의미하게 되었고 여기에 0~1 사이의 값을 가지는 임계값을 설정하여 사건이 발생할 확률이 어느 이상이어야 결과(y)를 1로 할지 결정한 뒤, 이를 최적화하는 학습 계수들을 학습하면 된다.
- z=0일 때, μ=0.5
- z>0일 때, μ>0.5이면 \( \hat y \)=1
- z<0일 때, μ<0.5이면 \( \hat y \)=0
즉, z가 분류 모형의 판별 함수(decision function)의 역할을 한다. 로지스틱 회귀분석에서는 판별 함수 수식으로 선형 함수를 사용한다. 이렇게 z를 이용해 y가 0 또는 1이 되는 것을 정하는 기준인 결정 경계(Decision boundary)를 정한다.

비용 함수(Cost Function) or 손실 함수(Loss Function)
다음은 비용(cost) 함수이다. 이는 w, b의 값을 찾기 위한 함수이다. 일반적으로 경사 하강법(Gradient Descent)을 사용하기에 적합한 함수 모양으로 만들어야 한다. 일반적인 Regression의 비용 함수는 \( \sum(예측값-실제값)^2 \)으로 계산하는 최소 제곱합(MSE)과 같이 2차 함수의 형태로 만들어 경사 하강법을 적용한다.
아래는 일반 회귀 모델의 비용 함수이다.
$$ cost = \frac{\sum_{i=1}^{n}(\hat{y}_i-y_i)^2}{n} $$

여기서 \( \hat{y} \)는 예측값 \( y \)는 원본 데이터 값이다. 하지만 로지스틱 회귀의 비용(손실) 함수는 달라야 한다. 자연상수 e에 의해 MSE는 2차 함수의 일반적인 모양을 띄지 않아 지역 최소(local minimum) 문제를 야기하기 때문이다. 이는 실제 최소 지점이 아님에도 다른 골짜기 부분을 최소 지점이라 생각하는 문제이다. 이를 상쇄하기 위해 log를 씌워주는 과정이 추가된다.
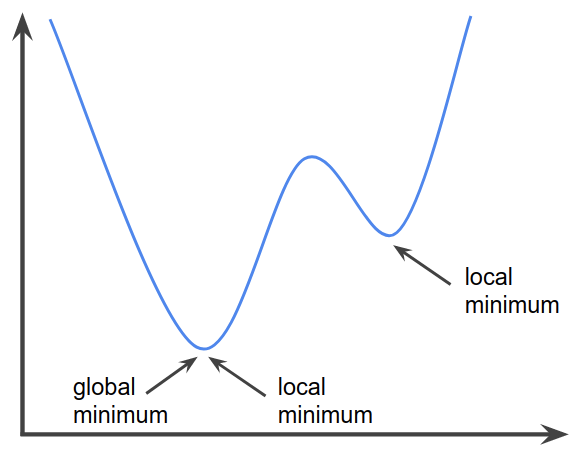
이진 교차 엔트로피(Binary Cross Entropy)
그러므로 로지스틱 회귀는 아래 수식을 손실 함수로 사용한다. 이 손실 함수가 이진 교차 엔트로피(Binary Cross Entropy)이다.
$$ cost=\frac{1}{n}\sum_{i=1}^{n}{(-y_ilog(wx_i+b)-(1-y_i)log(1-wx_i+b)} $$
이 손실함수는 최대 우도법(maximum likelihood estimation)에서 유래되었다. 로그 우도함수(log-likelihood function)를 최대로 하는 회귀계수는 동시에 우도를 최대화하며 그 역도 성립한다.
손실 함수를 계산했다면 다른 회귀 모델처럼 이 비용 함수의 값을 최소화해야 한다. 이를 위한 가장 대표적인 방식이 경사 하강법(Gradient Descent)이다. 경사 하강법은 옵티마이저(optimizer) 중 하나인데 글이 너무 길어지므로 옵티마이저의 존재만 인지하고 넘어간다. 결과적으로 \(w=w-(\frac{∂L}{∂w}) \)와 \(b=b-(\frac{∂L}{∂b}) \)와 같이 각각 편미분을 가중치와 절편을 업데이트하는데 이 과정은 일반 선형 회귀와 동일하다.
어차피 지금 증명을 한 것도 아니고 수식과 관련된 부분은 잘 모르겠으면 그냥 넘기면 된다. 개인적으론 데이터 분석 업무를 하며 여러 수식을 마주하면, 해당 과정이 어떠한 의미를 지니는지만 제대로 파악하고 파이썬을 이용해 관련 라이브러리를 활용하여 넘어가는 편이다.
다음은 python을 이용한 로지스틱 회귀 구현이다.

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.e ** (-x))
def logistic_regression(data, learning_rate=0.01, epochs=1000):
w = 0.0
b = 0.0
for i in range(1, epochs+1):
for x, y in data:
w_difference = x*(sigmoid(w*x+b)-y)
b_difference = sigmoid(w*x+b)-y
w -= learning_rate*w_difference
b -= learning_rate*b_difference
if i%10==0:
print('epoch =', i, ', w =', round(w, 3), ', b =', round(b, 3))
print('epoch =', i, ', w =', round(w, 3), ', b =', round(b, 3))
return w, b
n = 20
x_data = np.linspace(0, n, n, dtype=int).reshape(-1, 1)
y_data = np.array([1 for i in range(n)]).reshape(-1, 1)
y_data[:int(n/2)] = 0
data = np.append(x_data, y_data, axis=1)
w, b = logistic_regression(data=data)
plt.scatter(x_data, y_data)
plt.plot(x_data, sigmoid(w*x_data+b))
plt.show()
데이터는 20개 learning rate는 0.01, epochs는 1000번으로 지정하고 학습을 수행하였다. w=0.829 , b=-7.282으로 산출되었다. 어떤 과정으로 로지스틱 회귀가 수행되는지 간단하게 알아볼 수 있게만 구현하였다. 따라서 지금의 데이터는 선형적으로 임시 생성하였기 때문에 결과에 큰 의미는 없다.
다음은 sklearn의 LogisticRegression 함수를 이용해 와인 등급을 맞추는 로지스틱 회귀 분석이다. 와인 등급은 임의로 0, 1, 2 세 가지이므로 이진 분류가 아닌 다중 분류(multi classification)로의 확장이다.
사용되는 데이터는 sklearn에서 제공해 주는 테스트 데이터 셋인데 이 와인 데이터에는 아래와 같은 수치가 있다.
['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols',
'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity',
'hue', 'od280/od315_of_diluted_wines', 'proline']
위 수치들을 이용해 로지스틱 회귀 분석을 수행한다.
LogisticRegression 함수의 하이퍼 파라미터(Hyper Parameter)는 간략하게 아래와 같다.
- penalty : 1차, 2차, 1차+2차 혼합, 미규제 중에서 복잡한 모델에 대한 규제 방법을 선택
'l1', 'l2', 'elasticnet', 'none'가 있고 default는 'l2'이다. - C : penalty에 대한 계수 설정, 기본 값은 1.0, 높을수록 복잡한 모델에 대한 규제 강화
- solver : solver : 로지스틱 회귀는 비선형 방정식이라 근사 알고리즘으로 접근하는데, 알고리즘의 종류 선택
특정 solver는 일부 penalty 방식을 지원하지 않을 수도 있음
‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’가 있고 default는 'lbfgs' - random_state : 근사 알고리즘의 초기 상태가 실행 시마다 달라질 수 있기 때문에 실행마다 결과를 고정하기 위해 임의의 정수를 설정하여 사용 가능
- max_iter : solver에 의해 진행되는 수렴을 위한 반복의 최대 횟수를 지정할 수 있는데 데이터와 solver에 따라 수렴이 오래 걸리는 경우가 있음
더 있지만 이정도만 설명하고 넘어간다. 아래는 python 소스 코드이다.
import pandas as pd
from sklearn import datasets # https://scikit-learn.org/stable/datasets/toy_dataset.html
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
wine_data = datasets.load_wine()
print(wine_data.feature_names)
# train, test 셋 분리
x = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)
y = wine_data.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, shuffle=True)
# 로지스틱 회귀 모델 학습
model = LogisticRegression(penalty='l2', max_iter=100)
model.fit(x_train, y_train)
for i, coef in enumerate(model.coef_):
res = sum(coef*x_test.iloc[0]) + model.intercept_[i]
print(i, "등급일 가능성 : ", res)
# 0 등급 가능성 : -2.3850845830146885
# 1 등급일 가능성 : -4.111530470738077
# 2 등급일 가능성 : 6.496615054227784
# 로지스틱 모델 학습 성능 비교
y_pred = model.predict(x_test) # 예측 결과 라벨
print("등급 : ", y_pred[0])
# 등급 : 2
# 정확도 측정
print(round(accuracy_score(y_pred, y_test), 3)*100, "%")
# 97.2 %
0, 1, 2등급이 될 가능성이 각각 w(coef_)와 b(intercept_)에 의해 도출되고 해당 회귀 식에서 2등급일 때가 가장 높다. 여기서 수치가 0~1 사이가 아닌 건 정규화(Normalization)를 수행하지 않았기 때문이다. 어쨌든 x_test의 첫 행의 데이터를 가진 와인은 2등급으로 "분류"된다. 해당 모델은 약 97.2%의 정확도로 분류를 해낸다.
하지만 위 코드 대로라면 아래의 경고가 나온다.
ConvergenceWarning: lbfgs failed to converge (status=1): STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
max_iter를 높게 설정해 주면 나오지 않지만 사실 이전에 전처리를 통해 데이터 정규화(Normalization)부터 수행해주어야 한다. 일단 이번에는 정규화 과정 없이 로지스틱 회귀만 구현해 보고 넘어간다.
정리하자면 로지스틱 회귀는 활성화 함수로 Sigmoid 함수를 사용해 종속 변수를 확률로 나타낸다는 것이다. 이 확률이 특정 임계값(일반적으로 0.5)을 넘으면 1 아니면 0인 이진 분류를 수행한다. 대상이 여러 개인 다중 분류로 확장하면 각 클래스 별 확률을 확인하고 가장 높은 확률의 클래스로 분류한다.
관련 포스트
2022.02.23 - [Data Science/Data Analysis] - [Python] 단순 선형 회귀(Simple Linear Regression, SLR)의 이해와 구현
2022.02.28 - [Data Science/Data Analysis] - [Python] 다항 회귀(Polynomial Regression)의 이해와 구현
2025.05.15 - [Data Science/Data Analysis] - Logit(로짓)과 Odds(오즈)
참고 자료
https://ratsgo.github.io/machine%20learning/2017/04/02/logistic/
https://hleecaster.com/ml-logistic-regression-example/
https://yamalab.tistory.com/79
https://towardsdatascience.com/optimization-loss-function-under-the-hood-part-ii-d20a239cde11
https://yoon1seok.tistory.com/34
소스 코드

