주요 개념
- 상관관계 분석(correlation analysis)
- 회귀 분석(Regression Analysis)
- 선형 회귀(Linear Rregression)
대표적인 데이터 분석 방법으로 예측에 이용되는 회귀 분석(Regression Analysis)과 상관계수를 이용한 상관관계 분석(Correlation analysis)이 있다.
- 연속형 또는 순위 자료로 이루어진 두 변수간 상호 관계 정도를 알아보고자 할 때는 상관관계 분석(correlation analysis)을 이용
- 두 변수간 인과 관계와 같이 한 변수가 다른 변수에 주는 영향력을 알아보고자 할 때는 회귀 분석법(regression analysis)을 이용
그중 선형 회귀(Linear Rregression)는 종속 변수 y와 한 개 이상의 독립 변수 x와의 선형적 관계를 모델링하는 회귀분석 기법이다.
$$ y=wx+b $$
일반적으로 선형 회귀에서 기울기는 w(weight)로 y 절편은 b(bias)로 표현한다.
선형 회귀에도 두 가지 종류가 있는데, 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀(simple linear regression)와 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀(multiple linear regression)가 있다.
여기서 소개하는 단순 선형 회귀는 독립변수와 종속변수가 선형적인 관련성이 있다는 가정 하에 변수들 간의 관계를 선형 함수식으로 도출하기 위한 분석기법이다. 주어진 데이터와 오차가 가장 작은 일차방정식을 찾는 것이다.
선형 회귀에서 오차를 판단하기 위해 일반적으로 MSE(mean squared error)를 사용하는데, 보통 2차 곡선형태가 미분 편의성이 좋기 때문이다. 참고로 머신러닝에서는 오차를 손실(Loss) 또는 비용(Cost), 오차(Error)로 혼용해서 표기할 수 있고, 이 오차를 정의한 함수를 손실 함수(Loss function) 또는 비용 함수(Cost function), 오차 함수(Error function)라고 부른다.
오차 함수를 이용하여 오차를 도출한 뒤엔 반복적으로 최소 오차를 찾아나가는 loop 과정이 필요할 것이다. 이때 경사 하강법(Gradient Descent)을 사용한다. 경사하강법은 단순하게 말하면 임의의 파라미터를 정하고, 이를 조금씩 바꿔가며 오차를 점점 줄여가는 방향으로 이동해 최적의 파라미터를 산출하는 것이다.
경사 하강법을 진행할 때 얼마나 큰 보폭으로 움직이는지 정해주기 위해 학습률(learning rate)이 존재한다. 학습률이 너무 크면 overshooting이 되어 범위를 벗어날 수도 있고, 반대로 너무 작으면 최적 파라미터 탐색까지 너무 오랜 시간이 걸릴 것이다.

위 경사 하강법을 오차가 0일 때까지 반복하면 영원히 끝나지 않는 loop가 될 것이다. 따라서 수렴(Convergence)하는 부분이 필요하다. 계속 반복하다 보면 아래 그래프처럼 나름 최적의 값으로 수렴한다. 이때 반복 횟수는 epoch을 설정해서 정하면 된다. epoch도 너무 많이 돌리면 과적합(overfitting) 될 수 있다.

아래 python 코드를 이용해 데이터를 생성한다.
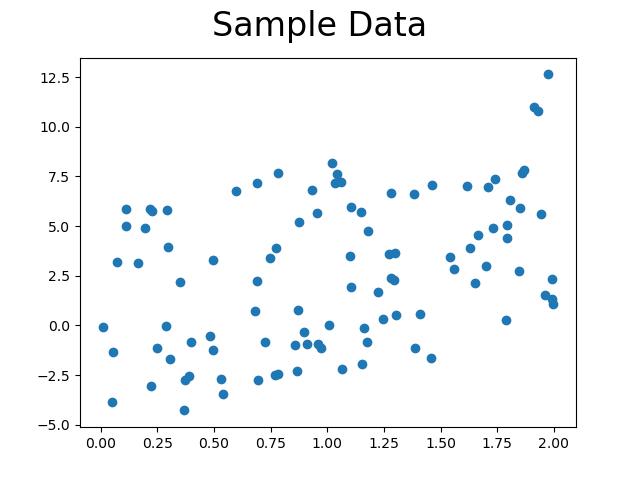
def make_data(size=100, noise=1):
x = 2*np.random.rand(size, 1)
y = 3*x+np.random.randn(size, 1)
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
plt.scatter(x, yy)
plt.suptitle("Sample Data", size=24)
plt.show()
return x, yy
이후 단순 선형 회귀를 이용해 샘플 데이터를 가장 잘 설명하는 1차 방정식을 도출한다. 결과에 대한 평가를 위해 결정계수(\(R^2\))와 상관계수(Correlation), MSE 값을 이용해 보았다.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
def SLR(x, y, epochs=5000, learning_rate=0.01):
w = 0.0
b = 0.0
n_data = len(x)
for i in range(epochs):
hypothesis = w*x+b
cost = np.sum((hypothesis-y)**2)/n_data
gradient_w = np.sum((w*x-y+b)* 2*x)/n_data
gradient_b = np.sum((w*x-y+b)*2)/n_data
w -= learning_rate * gradient_w
b -= learning_rate * gradient_b
if i % 100 == 0:
print('Epoch ({:10d}/{:10d}) cost: {:10f}, W: {:10f}, b:{:10f}'.format(i, epochs, cost, w, b))
return w, b, w*x+b
x, y = make_data(size=100, noise=6)
w, b, res = SLR(x, y)
data = np.concatenate((x, y, res), axis=1)
df = pd.DataFrame(data, columns=['x', 'y', 'predict'])
print("결정계수: ", r2_score(y, res))
print("상관계수: \n", df.corr())
print("MSE: ", mean_squared_error(y, res))
# 결정계수: 0.25375636333562246
# 상관계수:
# x y predict
# x 1.000000 0.411021 1.000000
# y 0.411021 1.000000 0.411021
# predict 1.000000 0.411021 1.000000
# MSE: 10.83416113560029
아래는 sklearn 라이브러리의 LinearRegression 함수를 사용해 구현한 내용이다. LinearRegression 함수에서 weight를 positive로만 도출하거나, intercept(bias 값) 없이 파라미터 산출 여부 등 여러 옵션을 설정할 수 있다.
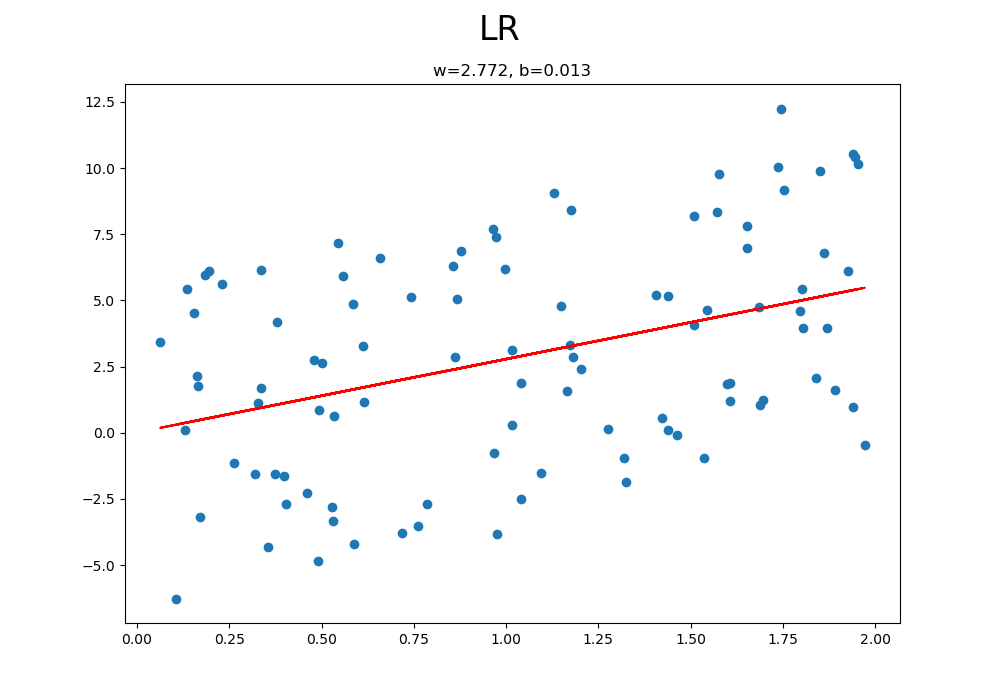
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
def LR(x, y):
model = LinearRegression()
model.fit(x, y)
res = model.coef_[0]*x + model.intercept_[0]
print('w: ', model.coef_[0][0], ", b:", model.intercept_[0])
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.plot(x, res, color='red')
plt.suptitle("LR", size=24)
plt.title('w=' + str(np.round(model.coef_[0][0], 3))+', b=' + str(np.round(model.intercept_[0], 3)))
plt.show()
return model.coef_[0][0], model.intercept_[0], res
x, y = make_data(size=100, noise=6)
_, _, res = LR(x, y)
data = np.concatenate((x, y, res), axis=1)
df = pd.DataFrame(data, columns=['x', 'y', 'predict'])
print("결정계수: ", r2_score(y, res))
print("상관계수: \n", df.corr())
print("MSE: ", mean_squared_error(y, res))
# 결정계수: 0.1558744895694929
# 상관계수:
# x y predict
# x 1.000000 0.411021 1.000000
# y 0.411021 1.000000 0.411021
# predict 1.000000 0.411021 1.000000
# MSE: 14.462941167790634
MSE는 직접 구현한 선형 회귀 모델이 좋다. LinearRegression 함수에서 파라미터를 수정하며 성능을 올려보는 시도를 해보면 좋을 것 같다.
아래는 전체 python 소스 코드이다.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
def make_data(size=100, noise=1):
x = 2*np.random.rand(size, 1)
y = 3*x+np.random.randn(size, 1)
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
plt.scatter(x, yy)
plt.suptitle("Sample Data", size=24)
plt.show()
return x, yy
def SLR(x, y, epochs=5000, learning_rate=0.01):
w = 0.0
b = 0.0
n_data = len(x)
for i in range(epochs):
hypothesis = w*x+b
cost = np.sum((hypothesis-y)**2)/n_data
gradient_w = np.sum((w*x-y+b)* 2*x)/n_data
gradient_b = np.sum((w*x-y+b)*2)/n_data
w -= learning_rate * gradient_w
b -= learning_rate * gradient_b
if i % 100 == 0:
print('Epoch ({:10d}/{:10d}) cost: {:10f}, W: {:10f}, b:{:10f}'.format(i, epochs, cost, w, b))
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.plot(x, w*x+b, color='red')
plt.suptitle("SLR", size=24)
plt.title('w=' + str(round(w, 3))+', b=' + str(round(b, 3)))
plt.show()
return w, b, w*x+b
def LR(x, y):
model = LinearRegression()
model.fit(x, y)
res = model.coef_[0]*x + model.intercept_[0]
print('w: ', model.coef_[0][0], ", b:", model.intercept_[0])
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.plot(x, res, color='red')
plt.suptitle("LR", size=24)
plt.title('w=' + str(np.round(model.coef_[0][0], 3))+', b=' + str(np.round(model.intercept_[0], 3)))
plt.show()
return model.coef_[0][0], model.intercept_[0], res
x, y = make_data(size=100, noise=6)
_, _, res = LR(x, y)
# w, b, res = SLR(x, y)
data = np.concatenate((x, y, res), axis=1)
df = pd.DataFrame(data, columns=['x', 'y', 'predict'])
print("결정계수: ", r2_score(y, res))
print("상관계수: \n", df.corr())
print("MSE: ", mean_squared_error(y, res))
관련 포스트
참고 자료
https://www.jeremyjordan.me/nn-learning-rate/
https://hleecaster.com/ml-linear-regression-concept/
https://m.blog.naver.com/istech7/50153288534
소스 코드

