주요개념
- VIF(Variance Inflation Factors)
- 다중공선성(Multicollinearity)
일반적으로 회귀분석은 독립 변수들을 선정하여야 한다. 이때 독립 변수 간 강한 상관관계가 나타나는 문제를 다중공선성문제(Multicollinearity)라고 한다. 이름에도 나와있듯 어떠한 독립 변수가 다른 독립 변수와 완전한 선형 독립이 아닌 경우를 말한다.

위의 그림처럼 독립 변수 n개를 이용하여 종속 변수 Y를 찾아내는 경우가 있다. 독립 변수들이 서로 상관관계가 높다면 결과를 도출하기 위한 데이터 분석 과정에서 부정적인 영향을 미치게 된다. 왜냐하면 독립 변수들의 영향력을 파악하여야 하는데 어떤 독립 변수 X1이 다른 독립 변수 X2에 영향을 미치고 있다면 우리가 원하는 "독립"된 변수가 아니기 때문이다. 이렇게 되면 예측할 결과에 대한 영향력을 검증할 때 통제할 수 없는 변수가 될 가능성이 있다.
예를 들어 축구선수의 시즌 종류 후 연봉 협상을 종속 변수 Y로 가정하자. 이 때 독립 변수 X1은 훈련량이라 하고, X2는 비만도라고 둔다. 이 때 X1은 X2와 상관관계가 크지 않다고 보기 힘들다. 적정 체중이 있을텐데 훈련을 많이 했는데도 비만이 된다는 것은 일반적인 상황에서 잘 일어나지 않기 때문이다. 이 독립 변수들을 가지고 회귀 분석을 수행하게 되면 X1이 증가한다면 Y가 증가할 것이고, X2가 증가한다면 Y는 감소하게 되는 것이 이상적이다. X1이 영향을 미치는 범위가 X2가 동시에 영향을 끼치게 될 것이고 분석 모형은 혼란스럽게 될 것이다. 결국 둘 중 하나는 유의한 변수가 될 것이고 하나는 통제하지 못하는 계수 값을 나타내게 된다.
이러한 다중공선성을 진단하는 방법은 다음과 같다.
- 결정 계수(상관 계수를 제곱한 것) \( R^2 \)값은 높아 회귀식의 설명력은 높지만 식 안의 독립변수의 P값(P-value)이 커서 개별 인자들이 유의하지 않는 경우가 있다. 이런 경우 독립변수들 간에 높은 상관관계가 있을 수 있다.
- 독립변수들 간의 상관 계수를 구해본다.
- 분산 팽창 요인(Variance Inflation Factor, VIF)을 구하여 이 값이 10을 넘는다면 보통 다중공선성의 문제가 있다.
다만 다중공선성이 있다면 상관관계는 높지만 이런 상관관계가 높다고 해서 무조건 다중공선성이 있다는 뜻은 아니다. 말장난 같이 느껴지지만 데이터 수가 충분하지 않은 경우 독립 변수간 상관관계는 높지만 다중공선성은 없는 경우도 있다. 따라서 다중공선성이 높다는 것은 예측 결과 값의 신뢰구간이 넓게 형성될 수 있다고 해석할 수 있다.
하지만 모든 독립 변수들이 완전한 선형 독립인 상태로 회귀 모형에 넣는 것은 쉽지않다. 모든 것은 대체로 유기적이고 완전한 독립들을 찾다 보면 넣을 독립 변수가 그리 많지 않을 수 있기 때문이다. 이번에도 역시 문제를 해결하기 위한 기준 수치가 필요하다. 이 다중공선성의 판단 기준이 되는 수치가 위에서도 잠깐 언급된 VIF(Variance Inflation Factors)이다.
각 독립 변수마다 VIF를 보고 10 이상인 경우 다중공선성이 있다고 판단할 수 있다. 더 엄격하게 기준을 잡는다면 VIF 수치 5 이상일 때 다중공선성 문제가 있다고 하는 경우도 있다. 예를 들어 독립 변수 a와 b가 서로 상관관계가 있다고 했을 때 두 변수 모두 높은 VIF 수치를 보여주게 된다. 어느 하나만 VIF가 높은 경우는 존재하지 않는다. 박수도 오른손과 왼손이 있어야 칠 수 있듯 서로 연관 있는 변수끼리 VIF가 높다. VIF의 수식은 아래와 같다.
$$ VIF_i = \frac{1}{1-R^2_i} $$
이 VIF 수치를 확인한 후 다중공선성 문제를 해결하기 위한 방법으로는 아래와 같이 4가지가 있다.
- 다중공선성을 가지는 독립 변수중 하나 혹은 일부를 제거한다. 단, 회귀 모형의 \( R^2 \) 값을 유지 또는 개선시키는 방향으로만 수행하여야 한다.
- 변수를 변형시키거나 새로운 관측치를 이용한다.
- 자료를 수집하는 현장의 상황을 보아 상관관계의 이유를 파악하여 해결한다.
- 주성분 분석(Principle Component Analysis, PCA)을 이용한 diagonal matrix의 형태로 공선성을 없애준다.
하지만 VIF 수치 또한 절대적인 독립 변수 도출 기준이 될 수는 없다. 이 VIF 값만 보고 단순하게 데이터를 모두 지워버린다면 우리가 원하는 인사이트를 도출할 수 없을 것이다.
아래는 python을 이용하여 다중공선성 파악을 위한 산점도를 그려보았다. 후보 독립 변수들은 꽃게의 키, 넓이, 껍질 무게, 내장 무게, 껍데기 무게이고 종속 변수는 꽃게의 나이로 둔다. 데이터는 아래와 같다.

일부러 다중공선성을 더 강조해보려 무게 관련된 것만 독립 변수로 선정해보았다.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('CrabAgePrediction.csv')
sns.pairplot(df[['Height', 'Weight', 'Shucked Weight', 'Viscera Weight', 'Shell Weight']])
plt.show()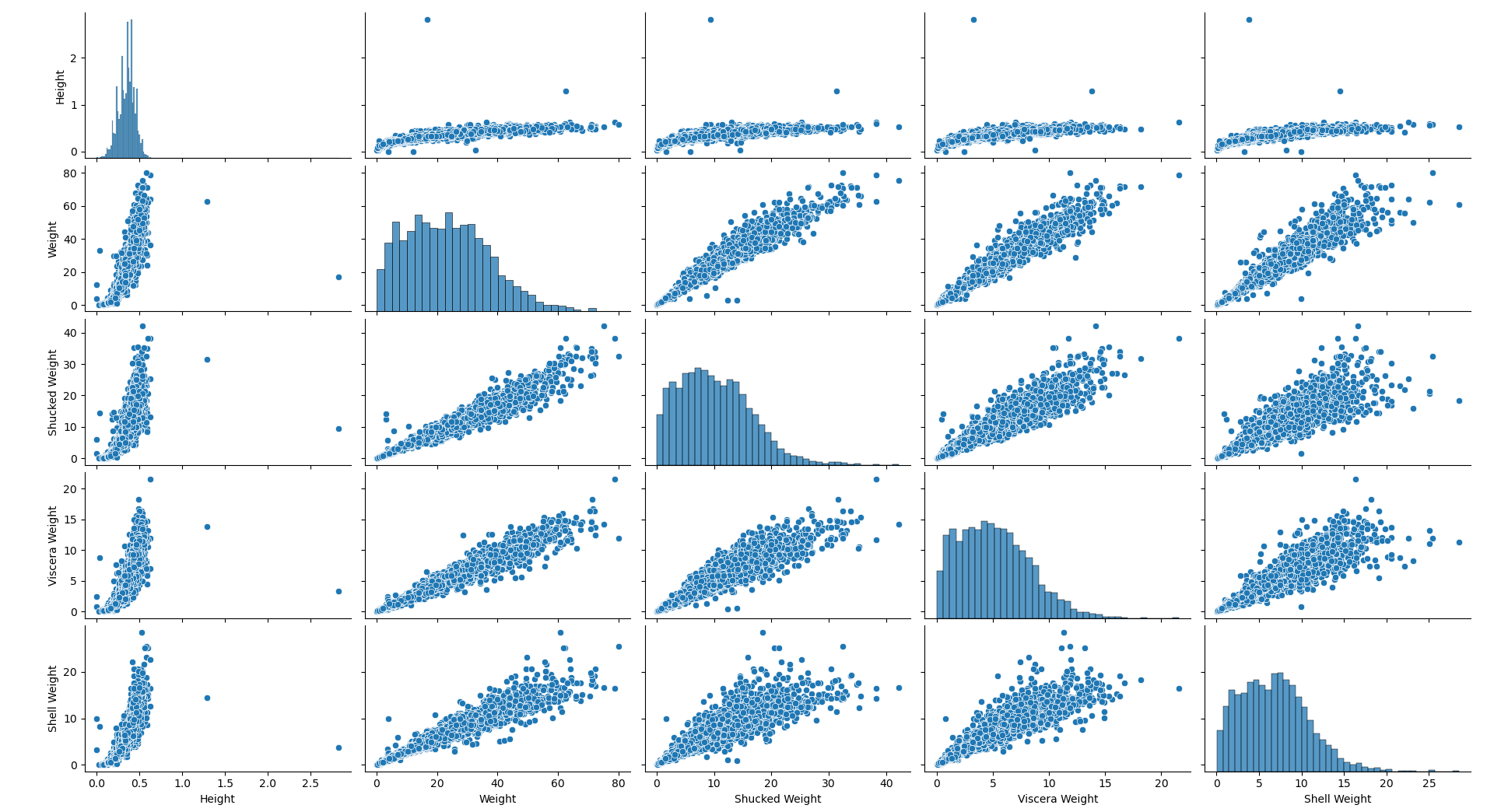
얼핏 봐도 키 말고는 전부 상관관계가 커 보인다.
아래는 다중공선성 문제가 있는 독립 변수들을 제거하지 않고 회귀 분석을 진행한 코드와 결과이다. 참고로 intercept는 절편인데 일반적으로 넣어준다.
import pandas as pd
import statsmodels.api as sm
df['intercept'] = 1
model = sm.OLS(df['Age'], df[['intercept', 'Height', 'Weight',
'Shucked Weight', 'Viscera Weight', 'Shell Weight']])
results = model.fit()
print(results.summary()) OLS Regression Results
==============================================================================
Dep. Variable: Age R-squared: 0.509
Model: OLS Adj. R-squared: 0.508
Method: Least Squares F-statistic: 805.6
Date: Tue, 28 Dec 2021 Prob (F-statistic): 0.00
Time: 00:43:43 Log-Likelihood: -8692.8
No. Observations: 3893 AIC: 1.740e+04
Df Residuals: 3887 BIC: 1.744e+04
Df Model: 5
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
intercept 5.4021 0.142 38.154 0.000 5.125 5.680
Height 6.8135 0.609 11.185 0.000 5.619 8.008
Weight 0.3351 0.027 12.457 0.000 0.282 0.388
Shucked Weight -0.6748 0.030 -22.498 0.000 -0.734 -0.616
Viscera Weight -0.2854 0.048 -6.001 0.000 -0.379 -0.192
Shell Weight 0.3869 0.041 9.368 0.000 0.306 0.468
==============================================================================
Omnibus: 784.284 Durbin-Watson: 1.991
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2609.815
Skew: 1.002 Prob(JB): 0.00
Kurtosis: 6.475 Cond. No. 539.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
키의 coef가 6.8135로 양의 상관관계를 띄고 있으며 키가 클수록 꽃게 나이가 많다는 것을 의미한다. 정말로 키만 꽃게의 나이와 연관이 있다고 생각하기는 힘들다. 커지면 커질수록 무게도 늘어나기 마련이기 때문이다. 따라서 이는 왜곡된 결과를 도출해냈다고 판단할 수 있다.
아래는 VIF 수치를 확인하는 python 소스 코드와 결과이다.
import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
df = pd.read_csv('CrabAgePrediction.csv')
X_train = df[['Height', 'Weight', 'Shucked Weight', 'Viscera Weight', 'Shell Weight']]
def feature_engineering_XbyVIF(X_train):
vif = pd.DataFrame()
vif['VIF_Factor'] = [variance_inflation_factor(X_train.values, i)
for i in range(X_train.shape[1])]
vif['Feature'] = X_train.columns
return vif
vif = feature_engineering_XbyVIF(X_train)
print(vif) VIF_Factor Feature
0 10.009713 Height
1 411.350120 Weight
2 98.367558 Shucked Weight
3 62.118977 Viscera Weight
4 80.164597 Shell Weight
전부 VIF가 10이 넘어버렸다. 키와 껍데기 무게만 가지고 다시 한번 VIF를 산출해본다.
VIF_Factor Feature
0 9.460318 Height
1 9.460318 Shell Weight
좀 낫다. 그냥 이 두 개만 가지고 다시 한번 회귀 분석을 시도한다.
OLS Regression Results
==============================================================================
Dep. Variable: Age R-squared: 0.397
Model: OLS Adj. R-squared: 0.396
Method: Least Squares F-statistic: 1278.
Date: Tue, 28 Dec 2021 Prob (F-statistic): 0.00
Time: 01:01:29 Log-Likelihood: -9093.7
No. Observations: 3893 AIC: 1.819e+04
Df Residuals: 3890 BIC: 1.821e+04
Df Model: 2
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
intercept 5.6790 0.155 36.675 0.000 5.375 5.983
Height 3.9791 0.655 6.073 0.000 2.695 5.264
Shell Weight 0.4246 0.017 24.345 0.000 0.390 0.459
==============================================================================
Omnibus: 1122.142 Durbin-Watson: 1.961
Prob(Omnibus): 0.000 Jarque-Bera (JB): 3364.771
Skew: 1.484 Prob(JB): 0.00
Kurtosis: 6.454 Cond. No. 132.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
이전보다 모두 크게 수치가 변하지는 않았지만 키의 coef는 절반 정도로 줄어들었다. 아무래도 무게보다는 꽃게의 키가 좀 더 나이에 크게 관련이 있는 것 같다. 실제로 수치를 봐도 어느 정도 수긍은 가는 결과이다. 하지만 이 독립 변수들 만을 사용한 회귀 모델의 R-squared의 결과는 보시다시피 좋지 못하다. 심지어 VIF 수치를 확인하여 나름대로 다중공선성을 제거하였지만 그러기 이전의 수치보다도 부정적으로 결과가 도출되었다. 이러한 현상은 앞서 언급한 것처럼 VIF 수치에만 집중하여 무엇이 정말 중요한 데이터인지에 대한 분석이 부족했기 때문이다.
그리고 추가적으로 "[2] Standard Errors assume that the covariance matrix of the errors is correctly specified."라는 문구가 Notes 아래에서 발견된다면 VIF를 따로 확인해보지 않더라도 다중공선성이 발견되었다는 뜻으로 해석하면 된다.
아래는 전체 python 소스 코드이다.
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
df = pd.read_csv('CrabAgePrediction.csv')
sns.pairplot(df[['Height', 'Weight', 'Shucked Weight', 'Viscera Weight', 'Shell Weight']])
plt.show()
X_train = df[['Height', 'Shell Weight']]
def feature_engineering_XbyVIF(X_train):
vif = pd.DataFrame()
vif['VIF_Factor'] = [variance_inflation_factor(X_train.values, i)
for i in range(X_train.shape[1])]
vif['Feature'] = X_train.columns
return vif
vif = feature_engineering_XbyVIF(X_train)
print(vif)
df['intercept'] = 1
model = sm.OLS(df['Age'], df[['intercept', 'Height', 'Shell Weight']])
results = model.fit()
print(results.summary())
관련 포스트
2022.11.25 - [Data Science/Data Analysis] - [Python] 주성분 분석(Principle Component Analysis, PCA)
참고 자료
https://bkshin.tistory.com/entry/DATA-20-%EB%8B%A4%EC%A4%91%EA%B3%B5%EC%84%A0%EC%84%B1%EA%B3%BC-VIF
소스코드

