확률이란 모델 파라미터 값이 관측 데이터 없이 주어진 상태에서 랜덤한 출력이 일어날 가능성이고,
우도(가능도)는 특정 관측 결과가 주어진 상태에서 모델 파라미터 값들이 나타날 가능성이라고 볼 수 있다.
즉, 확률은 가능성, 우도(가능도)는 데이터가 특정 분포를 따를지에 대한 가능성이므로 서로 반대되는 개념이다.
확률(Probability)
먼저 확률(Probability)이란 확률 분포가 있을 때, 관측값 또는 관측 구간이 분포 안에서 어떤 확률을 보여주는지에 대한 값이다. 여기서 중요한 점은 주어진 확률 분포가 우선 존재한다는 것이다.
확률 분포(Probability Distribution)는 아직 실제로 나타나지 않은 상태인 확률 변수가 시행 결과에 따라 특정한 값을 가질 확률을 나타내는 함수를 의미한다. 예를 들어 주사위를 던지는 상황이 있다 가정했을 때 확률 변수의 확률 분포는 이산 확률 분포 중 이산 균등 분포가 된다. 이처럼 확률 분포는 어떤 종류의 값을 가지는가에 따라 이산 확률 분포(discrete probability distribution)와 연속 확률 분포(continuous probability distribution)가 있고 이 둘에 국한되지 않는 경우도 있다.
$$ Probability=P(관측값 |확률분포) $$
즉, 확률은 이 주어진 확률 분포를 고정시킨 후 관측치나 구간이 포함될 수치이다.
이 확률을 비교하기 위해 이산 확률 변수(discrete random variable)는 확률 변수에 대응하는 확률값이 있으므로 특정 관측치가 일어날 확률을 비교적 알기 쉽다. 예를 들어 주사위의 6가지 숫자 중 하나가 나올 확률이라면 6개 중 유한개 중 한 가지가 되므로 이러한 변수를 이산 확률 변수라고 한다.
연속 확률 변수(continuous random variable)에선 확률 밀도 함수(probability density function, PDF)를 이용할 수 있다. 따라서 특정 구간을 정한 후 그 넓이를 통해 확률값을 구할 수 있다. 연속 확률 변수란 시간, 길이 등 연속성을 지니는 변수인데 예를 들어 공을 던졌을 때 공이 도달하는 거리와 같은 특정한 '구간'에 대한 확률을 구하는 것이다. 이는 곧 한 구간 내 모든 임의의 점을 취할 수 있다는 뜻이다. 아래는 확률 밀도 함수의 수식이고, 여기서 전체 넓이는 1이다.
$$ P(a < X < b) = \int_{b}^{a} f(x)dx $$
아래는 확률 밀도 함수를 시각화하는 python 코드이다.
import scipy as sp
import scipy.stats
import matplotlib.pyplot as plt
import numpy as np
rv = sp.stats.norm(loc=0, scale=2) # 기댓값이 0, 표준 편차가 2
data = np.linspace(-10, 10, 300)
y = rv.pdf(data)
plt.plot(data, y, color='blue')
plt.fill_between(data, y, where=(2<data) & (data<6), interpolate=True, color='red')
plt.show()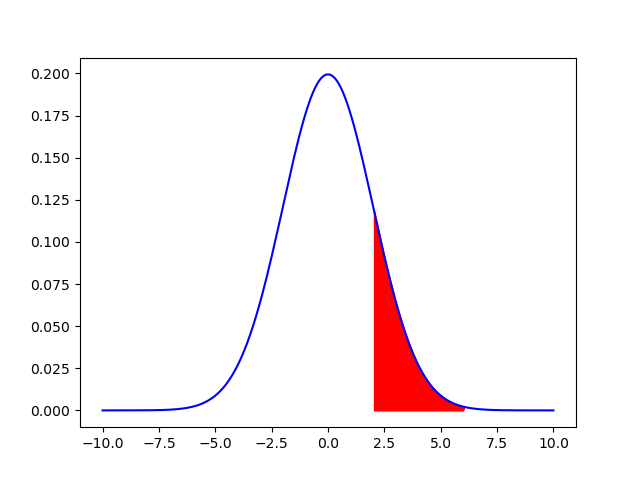
파란 선이 고정된 확률 분포이고 붉은 색이 칠해진 부분은 확률이다. 즉, 어떤 값이 \( 2<x<6 \)일 확률이다.
위의 그림 처럼 구간의 특정한 값을 가질 확률을 확인하게 되는데 특정 관측치의 확률은 0이 되는 부분이 있는 것을 확인할 수 있다. 이러한 특성에 의해 특정한 관측치가 일어날 가능성에 대해서는 비교하기 힘들다. 따라서 이를 알기 위해 가능도(우도, Likelihood)가 존재한다.
가능도(우도, Likelihood)
가능도(우도, Likelihood)는 원래 번역에서 우도라고 불렸는데 요즘엔 가능도라는 말로 자주 부르는 것 같다.
이산 확률 변수에선 특정 관측치에 대한 확률을 구할 수 있으므로 확률과 가능도가 큰 개념적 차이가 없다고 볼 수 있다. 하지만 가능도는 연속 확률 변수에서 확률과는 반대되는 의미를 지닌다.
확률은 주어진 확률 분포에서 어떤 관측값에 대한 참조 없이 결과가 일어날 가능성을 뜻하며 출력의 확률이라 볼 수 있다. 반면 가능도는 주어진 특정 관측값을 기반으로 특정 확률 분포에서 어떤 확률로 나타날 가능성을 말한다. 아래와 같이 확률과 조건부 순서가 반대이다.
$$ Likelihood=L(확률분포|관측값) $$
위는 이론적인 설명이고 좀 더 와닿으려면 예시만 보는 것이 나을 수도 있다.
먼저 주사위가 있고 짝수와 홀수가 나올 확률을 계산해보자. 이때 숫자 1이 적힌 면을 숫자 2로 바꾸면 홀수가 될 확률은 1/3이 되고 짝수가 될 확률이 2/3가 되어 확률을 비교하기가 쉽다. 이는 이산 확률 변수이기 때문이다.
만약 공을 던지고 공이 날아가는 거리를 보면 이미 지나쳐온 곳들을 다시 방문하지 않는 이상 그 거리에 다시 도달할 확률은 0이 된다. 또는 전 세계 사람들의 몸무게, 연간 이산화탄소 수치 등을 변수로 둘 수 있다. 이러한 연속적인 사건들을 가지는 것이 연속 확률 변수이고, 이는 연속 확률 분포를 보여주게 된다. 이를 위해 확률 밀도 함수가 있고 이 확률 밀도 함수에서 y값이 가능도이다.
만약 찌그러진 동전이 있다면 이 동전의 앞, 뒤가 나오는 확률은 50%가 아닐 가능성이 높다. 이에 대한 확률을 알기 위해선 실제로 던져봐야 할 것이다. 이러한 경우 진짜 확률을 추정해보기 위해 최대 가능도 추정을 수행한다.

