활성화 함수(Activation Function)란?
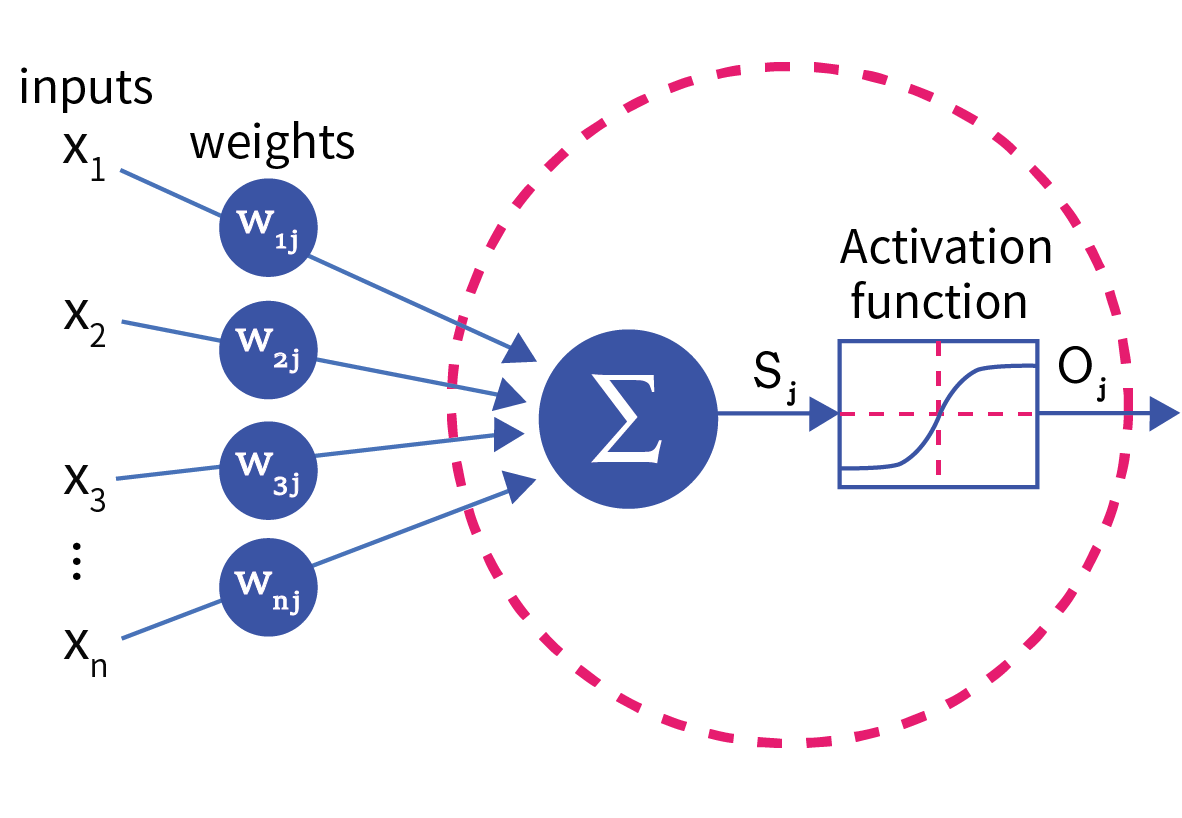
활성화 함수(Activation Function)는 딥러닝의 가중치를 구하기 위해 사용되는 비선형 함수(Nonlinear Function)이다. 이 활성화 함수는 딥러닝 네트워크에서 노드에 입력된 값들을 비선형 함수에 통과시킨 후 다음 레이어로 전달한다.
일단 가장 단순하게 대표적인 활성화 함수들의 역할을 정리해 보자면 다음과 같다.
- Sigmoid: 이진 분류 모델의 마지막 출력 계층(Output Layer)에 사용
- Softmax: 다중 분류 모델의 마지막 출력 계층(Output Layer)에 사용
- ReLU: 은닉층(Hidden Layer)에 주로 사용
왜 이런 비선형 함수들을 활성화 함수로 사용할까?
만약 선형 함수를 활성화 함수로 사용하게 된다면 간단한 계산과 모델 학습에서 가장 성가신 문제인 기울기 소실(Gradient Vanishing) 문제에서 해방될 수 있다는 장점이 있을 것이다.
하지만 딥러닝의 주요 목표는 다차원적이고 복잡한 데이터에서 비선형적인 관계를 학습하여 고차원적 특성을 추출하는 것이다. 선형 함수는 이러한 비선형적인 데이터의 특성을 학습하지 못하기 때문에, 신경망의 표현력을 극도로 제한하게 된다.
따라서 비선형 함수를 활성화 함수로 사용하여 아래와 같은 이점을 얻을 수 있다.
- 선형 모델의 한계 극복: 선형 모델은 각 입력의 특징을 선형적으로 해결하기 때문에 직선 형태의 결정 경계만 만들 수 있다. 이로 인해 복잡한 패턴이나 비선형적 관계를 가진 데이터에 적합하지 않다.
- 비선형성의 장점: 현실 세계의 데이터는 비선형적 관계와 복잡한 상호작용이 많다. 비선형 활성화 함수를 사용하면 신경망이 이러한 복잡한 데이터 패턴을 학습할 수 있으며, 더 높은 차원의 표현을 얻을 수 있다.
- 더 깊은(심층) 레이어의 학습: 비선형 활성화 함수 덕분에 신경망은 층을 쌓을수록 다양한 특성을 추출하고 복잡한 함수 근사화가 가능해진다.
쉽게 말하면 선형 모델에선 각 입력 데이터의 특징을 선형적으로 해결할 수밖에 없지만, 현실세계의 다차원의 특성을 지닌 데이터를 분류하기 위해서 비선형 활성화 함수를 사용한다는 것이다. 기본적으로 아래 조건들을 만족하는 함수 위주로 적용해 보는 것이 좋다.
- 비선형성 제공: 신경망의 학습을 위해 주로 비선형 활성화 함수가 사용되며, 이는 신경망이 단순한 선형 함수 이상의 복잡한 관계를 학습하도록 한다. 대표적인 비선형 활성화 함수로는 ReLU, Sigmoid, Tanh 등이 있다.
- 입력 값을 특정 범위로 제한: Sigmoid와 Tanh 같은 함수는 출력을 일정 범위로 제한하는 특징이 있어 출력 값이 특정 값에 수렴하도록 만든다. 예를 들어, Sigmoid는 [0, 1], Tanh는 [-1, 1] 범위로 출력한다.
- 기울기 소실(Gradient Vanishing) 방지: ReLU 같은 함수는 큰 출력 범위를 유지하면서 기울기 소실 문제를 방지하는 특징이 있어 깊은 신경망의 학습에 유리하다. 기울기 소실을 해결하지 못한다면 심층 구조를 구축하기가 쉽지 않다.
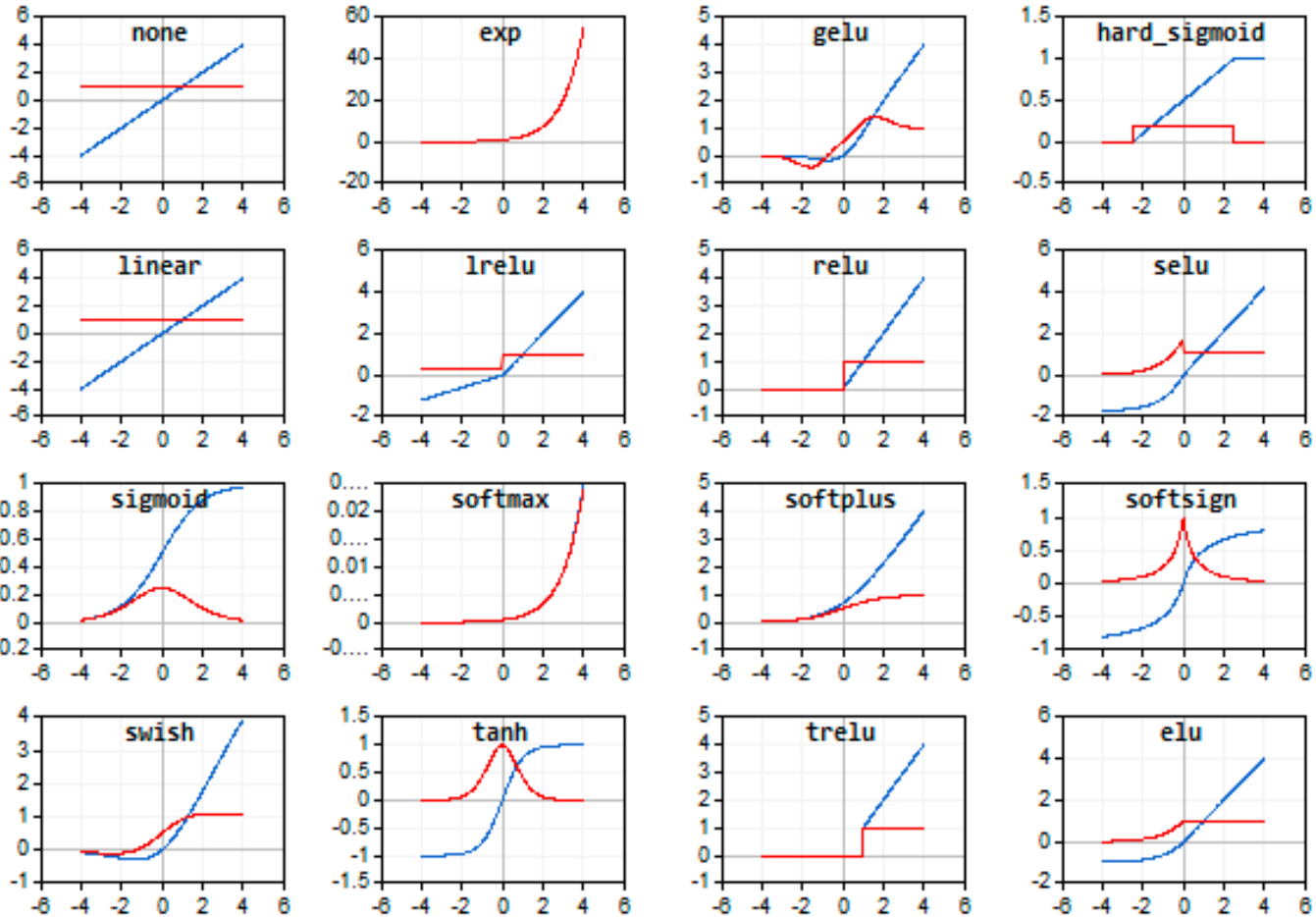
가장 대표적인 활성화 함수들을 아래에서 몇 가지 알아보자. 나름 발전 서사에 따라 진행하도록 노력해 보았다.
계단 함수
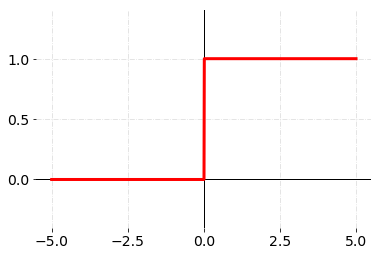
계단 함수는 가장 기본적인 비선형 함수이다. 입력 값이 임계값(Thresholding)을 넘기면 1, 그렇지 않으면 0을 출력하는 함수이다. 생물체의 전기적인 신호를 보낸다=1, 보내지 않는다=0의 형태로 대화하기 때문에 이를 모사하기 위하여 계단 함수가 고안되었다고 한다.
수식은 다음과 같다.
$$ f(x) = \begin{cases}
1 & \text{if } x \ge 0 \\
0 & \text{if } x < 0
\end{cases} $$
하지만 계단 함수는 -0.00001과 -100000000과 같은 결과에 대해 모두 0으로 평가해 버리기 때문에 활성화 함수로 사용하였을 때, 내부값의 차이를 오차에 제대로 반영할 수 없기에 학습 효율성이 좋지 못하다.
Sigmoid
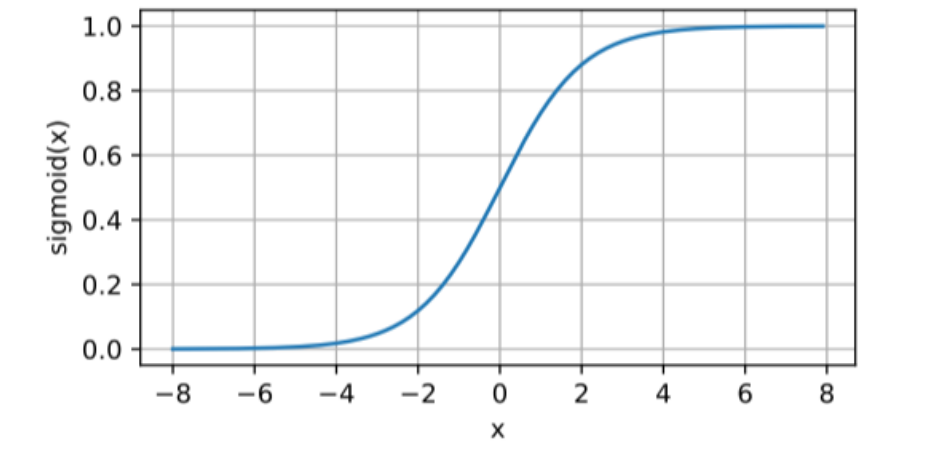
Sigmoid는 이진 분류 문제의 출력층에서 주로 사용하며, 입력값(x)에 대해 출력값의 범위가 0과 1 사이이다. 이를 통해 모델의 출력값을 해석하기 쉽게 만들어 준다.
수식은 다음과 같다.
$$ \text{sigmoid}(x) = \frac{1}{1 + \exp(-x)} $$
출력 범위: [0, 1]
형태를 보면 알 수 있겠지만 시그모이드는 앞서 언급된 계단 함수와 유사하다. 하지만 계단 함수에 비해 좀 더 smoothing 한 형태로 구현되어 학습 효율성을 좀 더 개선하였다.
또한 미분 가능한 형태가 되어 오차 역전파(Backpropagation) 과정을 좀 더 수월하게 진행할 수 있게 하여 가중치를 업데이트할 때 효율적으로 적용된다.
$$ \frac{d}{dx} \text{sigmoid}(x) = \text{sigmoid}(x) \cdot (1 - \text{sigmoid}(x)) $$
하지만 아래와 같은 단점이 존재한다.
먼저 특정 수준으로 결과값이 작아지거나 커지게 되면 기울기 소실(Gradient Vanishing)이 발생하여 가중치 업데이트가 중단되게 되는 문제가 있다.
뿐만 아니라 Non Zero-Centered 문제가 존재한다. 함수 출력이 0을 중심으로 하지 않아 신경망의 학습 과정에서 비효율을 발생 유발한다. 입력값의 범위가 -∞에서 +∞일 때 출력이 0에 집중되면서 비효율이 발생할 수 있기 때문이다.
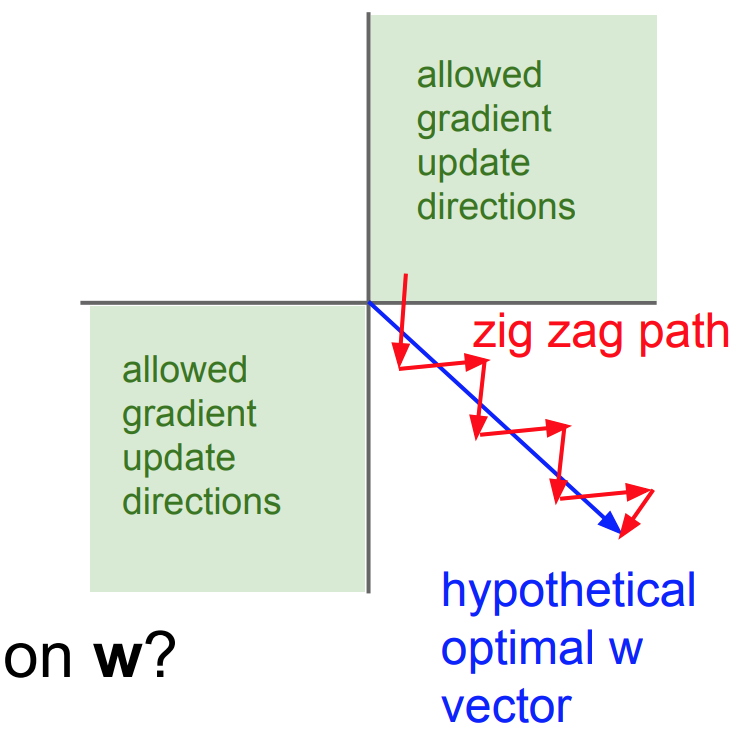
두 개의 양수 입력값과 2개의 가중치 1개의 결과로 수렴하는 모델이 있다고 가정하자. 여기서 새 가중치의 변화량은 현입력값과 오차의 곱이다.
이때 출력값의 오차가 음수가 된다면 두 가중치 변화량 모두 음수가 되고, 그 출력값의 오차가 양수라면 두 가중치 변화량 모두 양수가 될 것이다. 이 변화량이 동일하게 변하게 된다는 것은 결국 최적 가중치를 찾아가기 위해 직선적으로 움직이는 것이 아닌 우상단, 좌하단을 번갈아 움직이며 느리게 최적값에 수렴하게 되는 것을 말한다.
장점
- 계단 함수보다 Smooting 함
- 이진 분류에 적합
- 미분 가능한 형태
단점
- 기울기 소실
- Non Zero-Centered
- 연산 비효율성: 초창기엔 계산이 단순한 편이였지만 이후에 나온 ReLU와 같은 함수에 비해선 계산이 복잡
Tanh(Hyperbolic Tangent, Tanh)
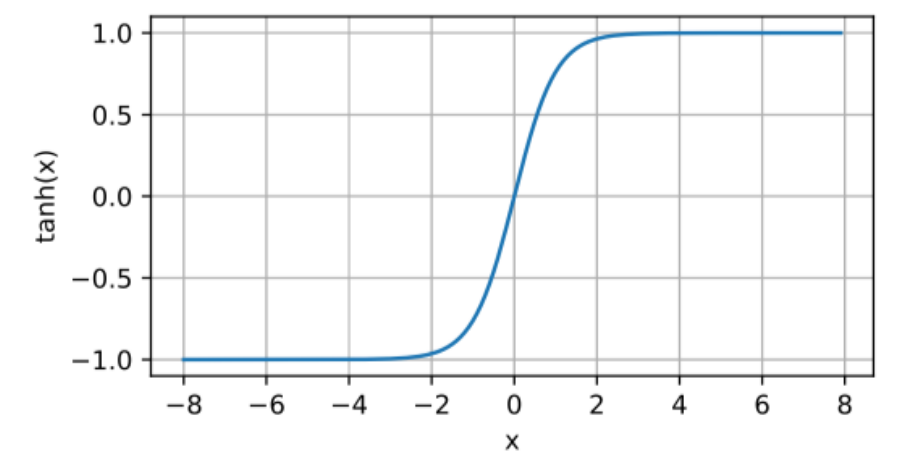
하이퍼볼릭 탄젠트(Hyperbolic Tangent, tanh) 함수는 실수 전체를 입력값으로 받을 수 있다. 이는 입력값이 어떤 값이든 상관없다는 것을 의미한다. Tanh 함수는 입력값을 -1과 1 사이의 값으로 "압축"한다. 즉, 매우 큰 양수는 1에 가까운 값으로, 매우 큰 음수는 -1에 가까운 값으로 변환된다. 이를 통해 앞서 언급한 Sigmoid의 Non Zero-Centered 문제점을 해결할 수 있다.
수식은 다음과 같다.
$$ \text{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)} $$
출력 범위: [-1, 1]
Tanh 함수의 유용한 특성 중 하나는 출력값이 0을 중심으로 대칭적이라는 것이다. 이는 신경망의 학습을 더 효율적으로 만들 수 있다. Tanh 함수의 미분은 다음과 같이 나타낼 수 있다.
$$ \frac{d}{dx} \text{tanh}(x) = 1 - \text{tanh}^2(x) $$
그러나 Tanh 함수에도 다음과 같은 단점이 존재한다.
- 기울기 소실(Gradient Vanishing): Tanh 함수 역시 깊은 신경망에서 기울기 소실을 유발
- 출력이 -1과 1 사이에 국한됨: 특정 문제에서는 출력 범위가 제한적
Softmax
Softmax는 주로 다중 클래스 분류 문제의 출력층에서 사용된다. 이 함수는 여러 클래스에 대한 확률 분포를 생성한다. Softmax 함수는 각 클래스에 대한 점수 \( z_i \)를 입력받아 확률을 출력한다.
수식은 다음과 같다.
$$ \text{softmax}(z_i) = \frac{\exp(z_i)}{\sum_{j=1}^{K} \exp(z_j)} $$
출력 범위: [0, 1] (모든 클래스의 출력 합이 1)
\( K \)는 클래스의 총개수와 동일하다. Softmax 함수의 유용한 특성 중 하나는 각 클래스의 확률이 0과 1 사이에 있는 점이다. 이 특성을 통해 모델은 각 클래스에 속할 확률을 추정할 수 있으며, 가장 높은 확률 값을 가진 클래스를 예측 결과로 선택할 수 있다. 따라서 모델의 출력을 확률로 변환하여 최종 예측을 가능하게 한다.
그러나 Softmax 함수도 아래와 같은 단점이 존재한다.
- 경쟁적 특성: 각 클래스의 확률을 계산할 때 서로 경쟁하게 함. 따라서 한 클래스의 확률이 높아지면 다른 클래스의 확률은 낮아짐
- 클래스 불균형: 클래스 불균형 문제를 해결하지 못함. 클래스가 불균형하게 분포된 경우, Softmax는 상대적으로 많은 데이터를 가진 클래스에 더 많은 가중치를 두게 되어 적은 데이터로 학습한 클래스의 예측 성능이 저하됨
ReLU(Rectified Linear Unit)
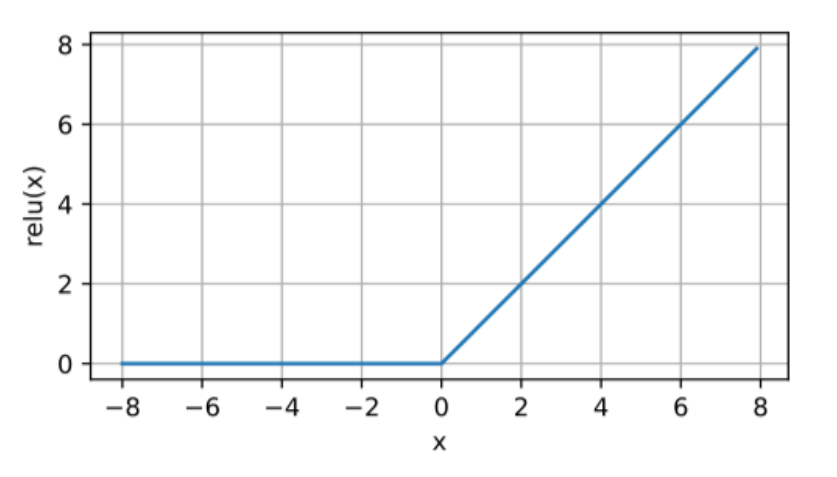
ReLU는 신경망의 은닉층에서 가장 널리 사용되는 활성화 함수이다. 입력값 \( x \)가 0 이하일 경우 0을 출력하고, 0 이상일 경우 \( x \)를 출력한다. 이 ReLU는 함수의 기울기가 양수일 때 항상 1로 고정되어 있어 Sigmoid나 tanh의 기울기 소실 문제를 어느 정도 해소해 주었다. 하지만 입력값이 음수일 때는 기울기가 0이므로 역시 기울기 손실에서 자유롭지는 못하게 된다.
수식은 다음과 같다.
$$ \text{ReLU}(x) = \max(0, x) $$
출력 범위: [0, ∞)
ReLU의 주요 장점은 다음과 같다.
- 간단한 미분: 미분이 간단하여 계산이 효율적
- 기울기 소실 문제 완화: 0 이상에서 기울기가 일정하므로 기울기 소실 문제 완화
그러나 ReLU 함수는 다음과 같은 단점이 존재한다.
- 죽은 뉴런(Dead Neurons) 문제: 입력값이 음수인 경우 뉴런이 비활성화되며, 이는 학습 과정에서 문제를 일으킬 수 있음
- 기울기 소실(Gradien Vanishing): Dead Neurons 문제로 인해 여전히 기울기 소실에서 자유롭지 못함
Leaky ReLU
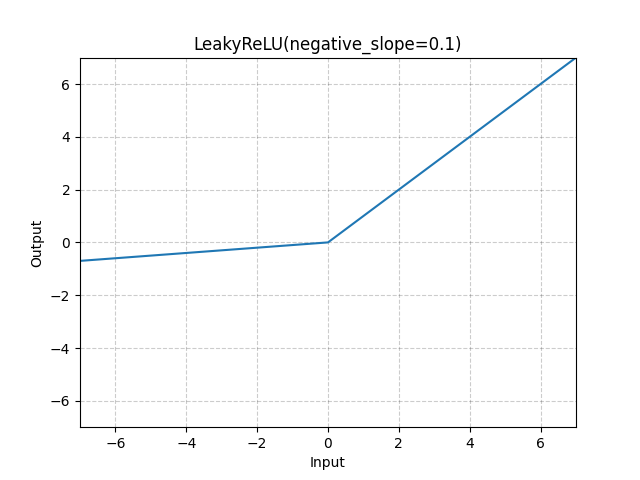
Leaky ReLU는 ReLU 함수의 변형으로, 입력값 \( x \)가 0 이하일 경우 작은 기울기를 갖도록 설정한다. 이를 통해 Dead Neurons 문제를 완화할 수 있다.
Leaky ReLU의 수식은 다음과 같다.
$$ \text{Leaky ReLU}(x) =
\begin{cases}
x & \text{if } x > 0 \\
\alpha x & \text{if } x \leq 0
\end{cases} $$
출력 범위: (-∞, ∞)
여기서 \( \alpha \)는 작은 상수로 보통 0.01이다.
Leaky ReLU는 음수 영역에서도 기울기가 존재하므로 뉴런이 비활성화되는 것을 방지하여 죽은 뉴런 문제를 해결할 수 있다.
하지만 Leaky ReLU 사용 시 학습 성능이 저하될 수 있다. 매우 작은 기울기로 인해 학습 속도가 느려질 수 있기 때문이다.
여러 가지의 활성화 함수가 존재하고 있고, 아직 완벽한 활성화 함수란 없는 것 같다. 각각 모델과 Layer의 특성에 맞는 활성화 함수를 적절히 적용하는 것이 중요하다 생각한다.
관련 포스팅
2024.10.27 - [Data Science/ML & DL] - Softmax에 대한 고찰
참고 자료
https://happy-obok.tistory.com/55
https://blog.naver.com/handuelly/221824080339
https://pytorch.org/docs/stable/generated/torch.nn.LeakyReLU.html
https://battlecoding.tistory.com/52
https://www.youtube.com/watch?v=iICZlmAhnf0

