옵티마이저(Optimizer)와 학습률(Learning Rate)

Optimizer

Fig 1. Optimizer

 

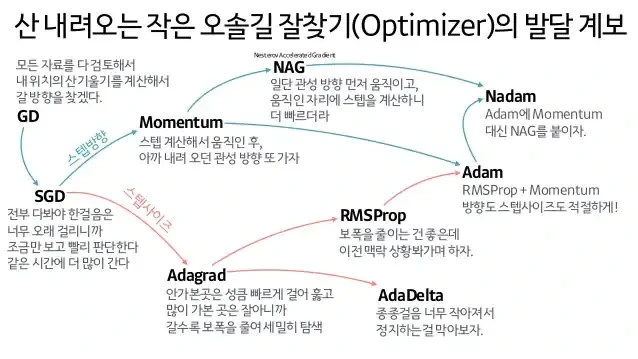
위 그림은 Optimizer를 설명하면 항상 빼놓지 않고 등장한다. 개인적으로 발전과정과 각 Optimizer의 특징이 간결하게 정리되어 있어서 완벽한 시각화 자료라고 생각한다.

 

옵티마이저(Optimizer)란 가중치를 갱신(Update) 하기 위한 방법이다.

 

Fig 2. Learning process of a neural network

 

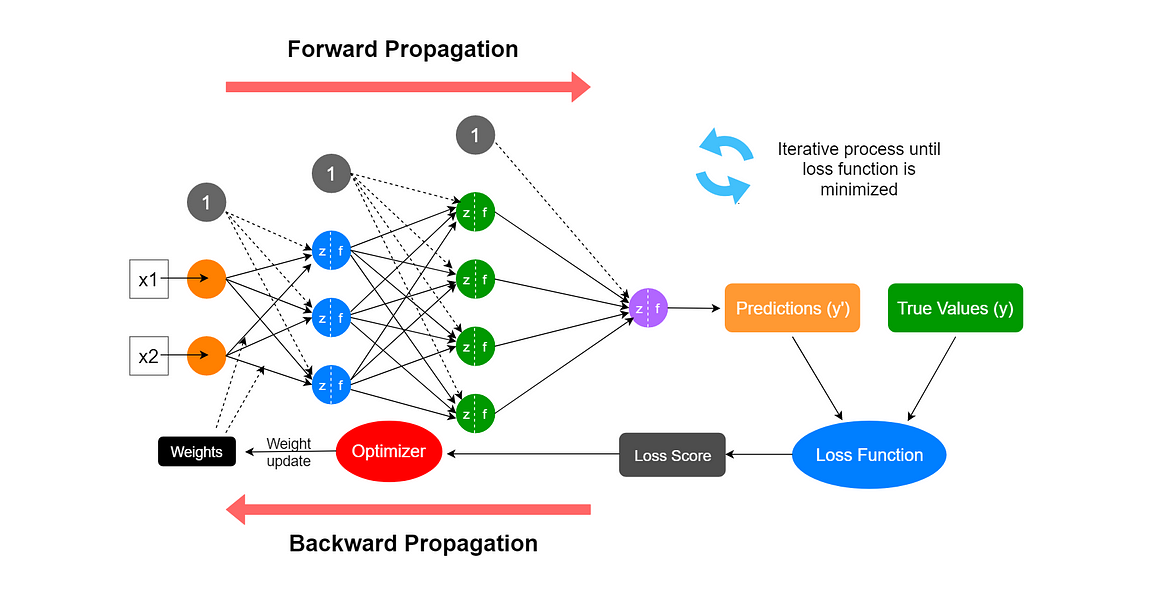
딥러닝 모델은 순전파(Forward Propagation) 과정에서 활성화 함수(Activation Function)를 거쳐 신경망의 가중치를 구한 후 최종 결과값과 실제 정답의 차이를 손실 함수(Loss Function)를 이용하여 계산한 한다.

 

그 후 역전파(Back Propagation) 과정을 수행하는데 이 때 가중치를 어떻게 업데이트할지 결정하기 위해 옵티마이저(Optimizer)가 사용된다. 이 과정을 반복하며 최적의 가중치(weight)를 가지는 모델을 찾아낸다. 옵티마이저는 손실을 최소화하기 위해 모델의 가중치를 조정하는 데 핵심적인 역할을 한다.

 

다시 말해 옵티마이저의 가장 큰 목적은 지역 최소값(Local Minima)에 빠지지 않고 손실을 최소화하는 가중치를 업데이트하는 것이다. 이 과정 중 여러 문제들을 해결해야 하는데 대표적으로 아래와 같은 것들이 있다.

• 학습 속도(Learning Rate) 조절: 학습률이 클수록 가중치 업데이트 폭이 커져 학습이 빨라질 수 있지만, 최적점을 놓칠 가능성이 커지고, 학습률이 너무 작으면 학습 속도가 느려져 수렴이 오래 걸리거나 지역 최소값에 갇힐 위험 발생
• 기울기 소실(Gradient Vanishing) 방지: Adam, RMSprop, Adagrad 이용하여 완화 가능
• 흔들림 현상(Oscillation)방지: 모델의 학습 과정에서 손실 함수가 줄어들지 않고 반복적으로 큰 폭으로 오르락내리락하는 상태
• 과적합(Overfitting) 방지: Weight Decay, Learning Rate Decay 등의 기법을 이용하거나 Adam, RMSprop 같은 옵티마이저를 사용하여 완화 가능

 

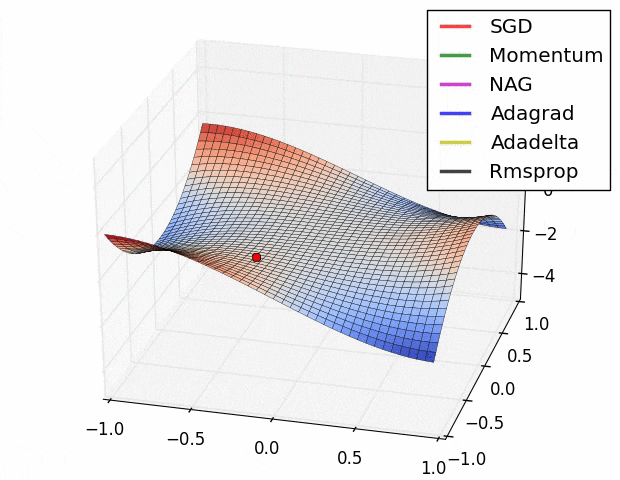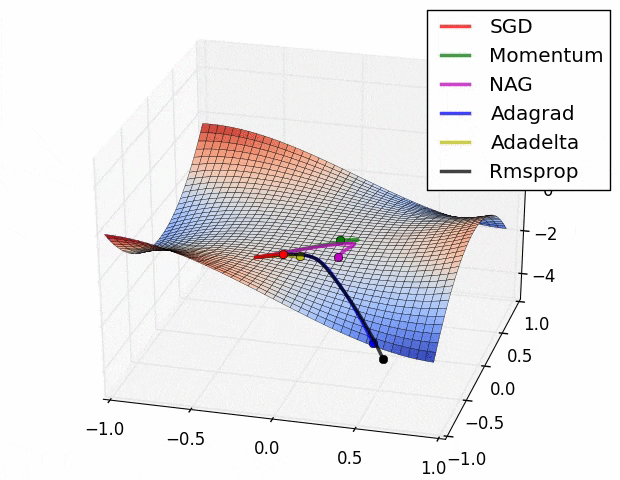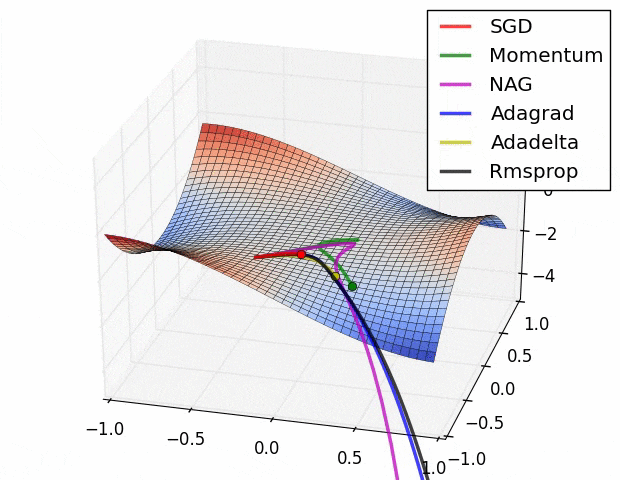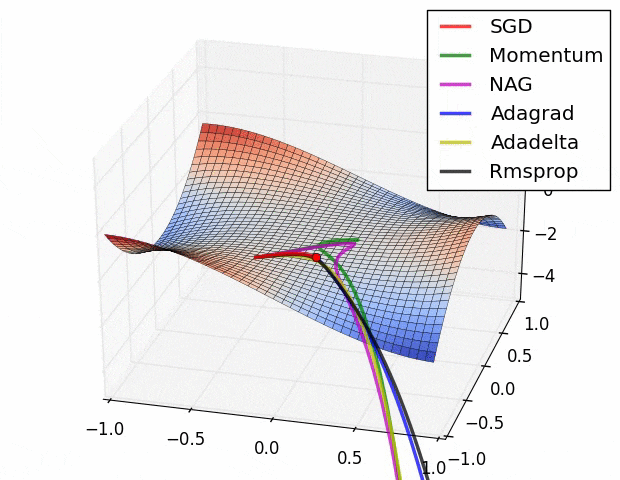
아래 그림은 앞으로 설명할 옵티마이저들이 Global Mima를 찾는 과정을 간단하게 시각화한 자료이다.

 

Fig 3. Optimizers

 

Learning Rate에 대한 이야기가 계속 나오는데 사실 이 Learning Rate(학습률)은 옵티마이저에서 빼놓을 수 없는 개념이므로 먼저 간단하게 설명하고 넘어간다.

 

Laerning Rate(학습률, \( \eta \))

Learning Rate는 딥러닝 모델을 학습할 때 가중치를 얼마나 크게 조정할지 결정하는 중요한 하이퍼파라미터이다. 학습 과정에서 손실 함수를 최소화하기 위해 매번 가중치를 업데이트하는데, 이때 학습률은 그 업데이트 크기를 조절하는 역할을 한다.

 

Learning Rate가 너무 크거나 작을 때의 문제점

• 학습률이 너무 클 때
  : 학습률이 너무 크면 손실 함수의 최저점을 놓치고 지나쳐서, 훈련이 불안정해질 수 있다. 이는 모델이 수렴하지 않거나, 높은 손실 값에서 오락가락하며 불안정하게 학습될 가능성을 높인다. 이렇게 되면 결국 가중치는 발산하게 되고 기울기 폭주(Gradient Explode) 상태가 되게 된다. 이런 경우를 Oveshooting이라고 한다.
• 학습률이 너무 작을 때
  : 학습률이 너무 작으면 모델이 수렴하더라도 시간이 오래 걸리고, 지역 최소점에 빠져 전역 최적점을 찾지 못할 수도 있다. 이는 학습이 느려지고, 자칫하면 최적화 성능이 떨어질 위험이 있다.

 

Learning Rate 조정 방법

• 고정 학습률
  : 처음부터 학습률을 하나로 설정하고 훈련이 끝날 때까지 변하지 않게 하는 방법이다. 하지만 이렇게 할 경우, 초반이나 후반에 성능이 떨어질 수 있다.
• Learning Rate Decay
  : 학습이 진행될수록 학습률을 조금씩 줄여 나가는 방식으로, 학습 초반에는 빠르게 탐색하고, 학습이 진행되면서 세밀하게 조정하여 안정적으로 최적화할 수 있게 한다.
• 적응형 학습률(Adaptive Learning Rate)
  : Adam, RMSprop 같은 옵티마이저가 이에 해당하며, 학습 중 기울기 변화에 맞춰 가중치별 학습률을 자동으로 조절한다. 이는 최적의 학습률을 유지하면서 과적합을 줄이는 데 효과적이다.
• Warm-up 및 Cool-down 기법
  : 처음에는 학습률을 점차 증가시키다가 이후에는 일정하게 유지하거나 줄이는 방식으로 학습을 시작할 수 있다. 초기 탐색과 세밀한 조정을 혼합해 효과적인 학습률 설정이 가능해진다.

학습률은 모델의 학습 성능에 직접적인 영향을 미치기 때문에 최적의 학습률을 찾는 것이 중요하다. 보통 학습률 스케줄링이나 적응형 옵티마이저와 같은 방식을 통해 효율적인 학습을 도모할 수 있다.

 

이제 각 옵티마이저들의 특징과 발전해 온 역사를 간략하게 살펴보자. 참고로 아래 Optimizer들의 수식에서 \( \eta \)는 학습률에 해당한다. 

 

Optimizer의 종류

(Vanila) Gradient Descent(GD) or Batch Gradient Descent(BGD)

Fig 4. Gradient Descent

 

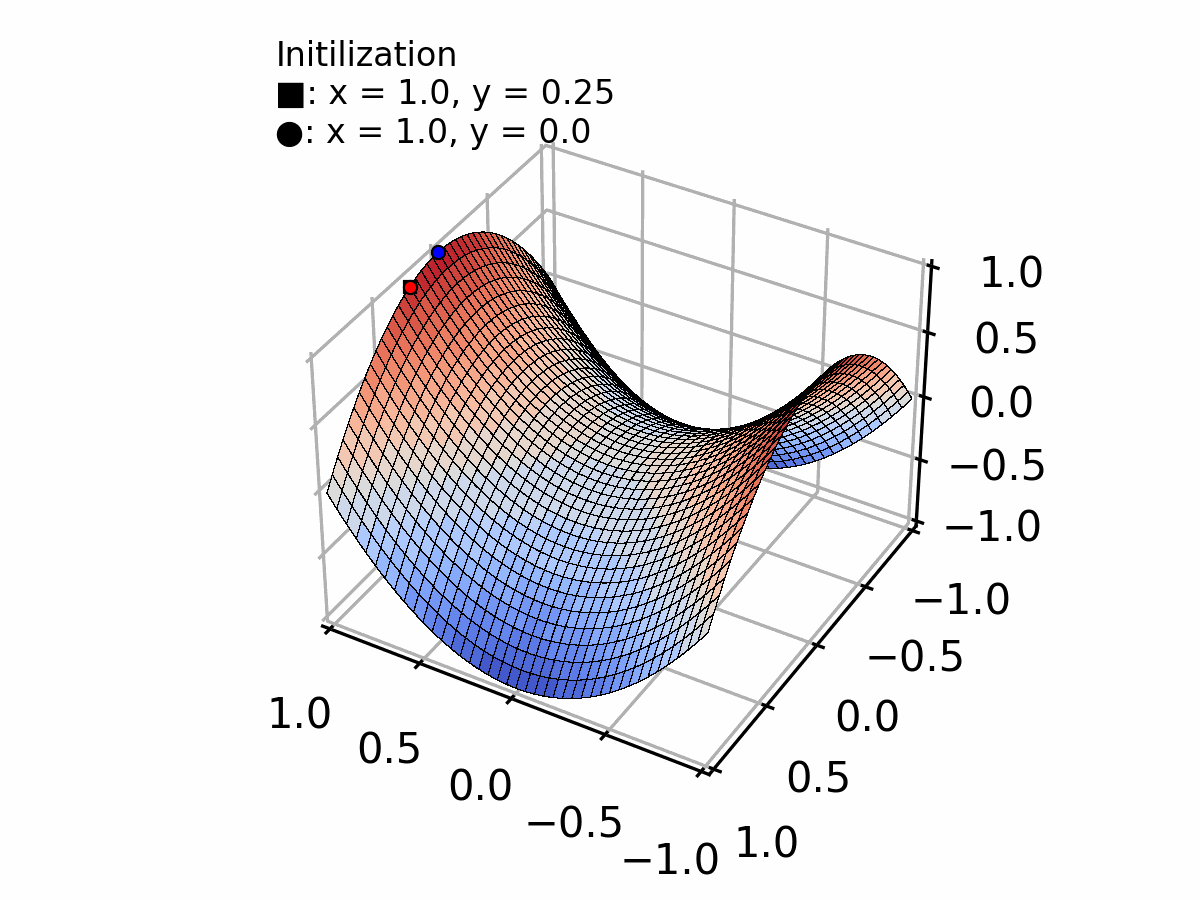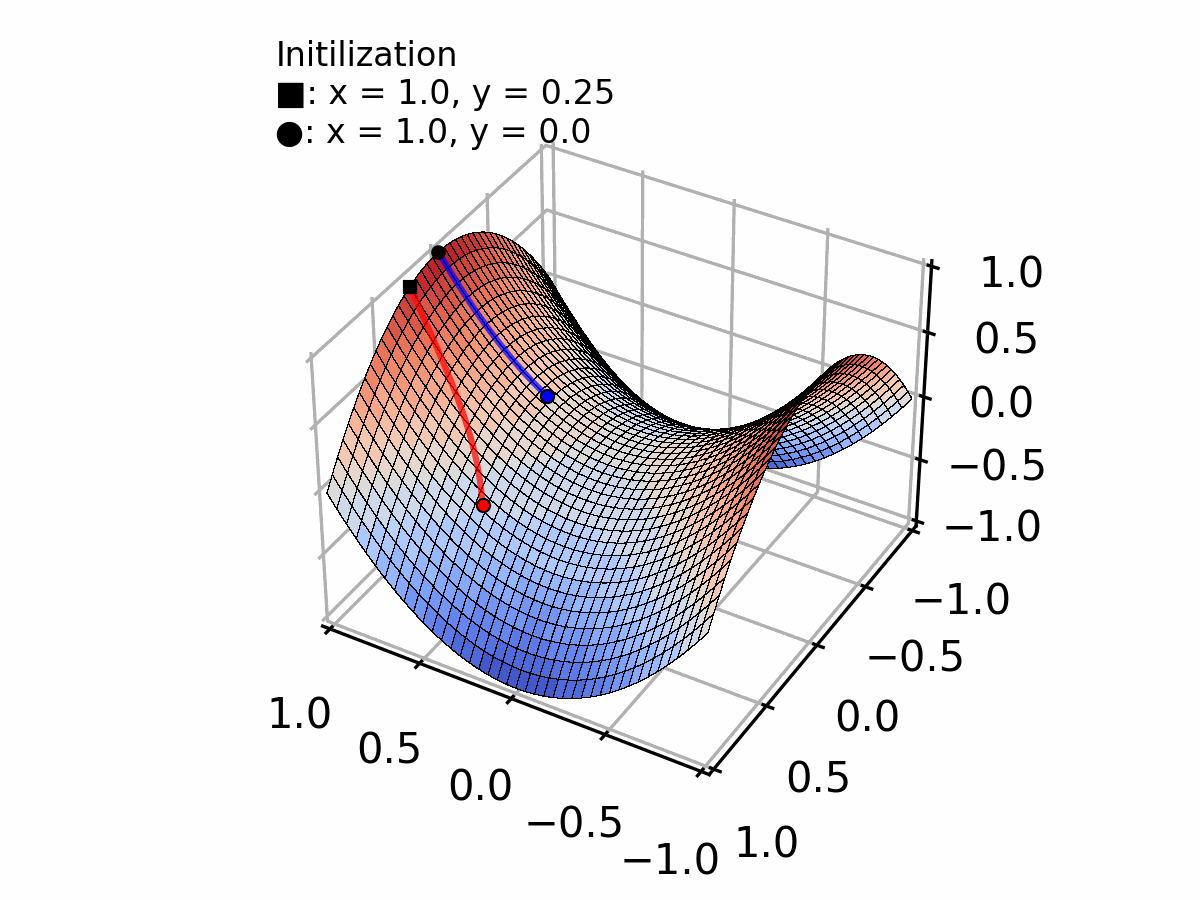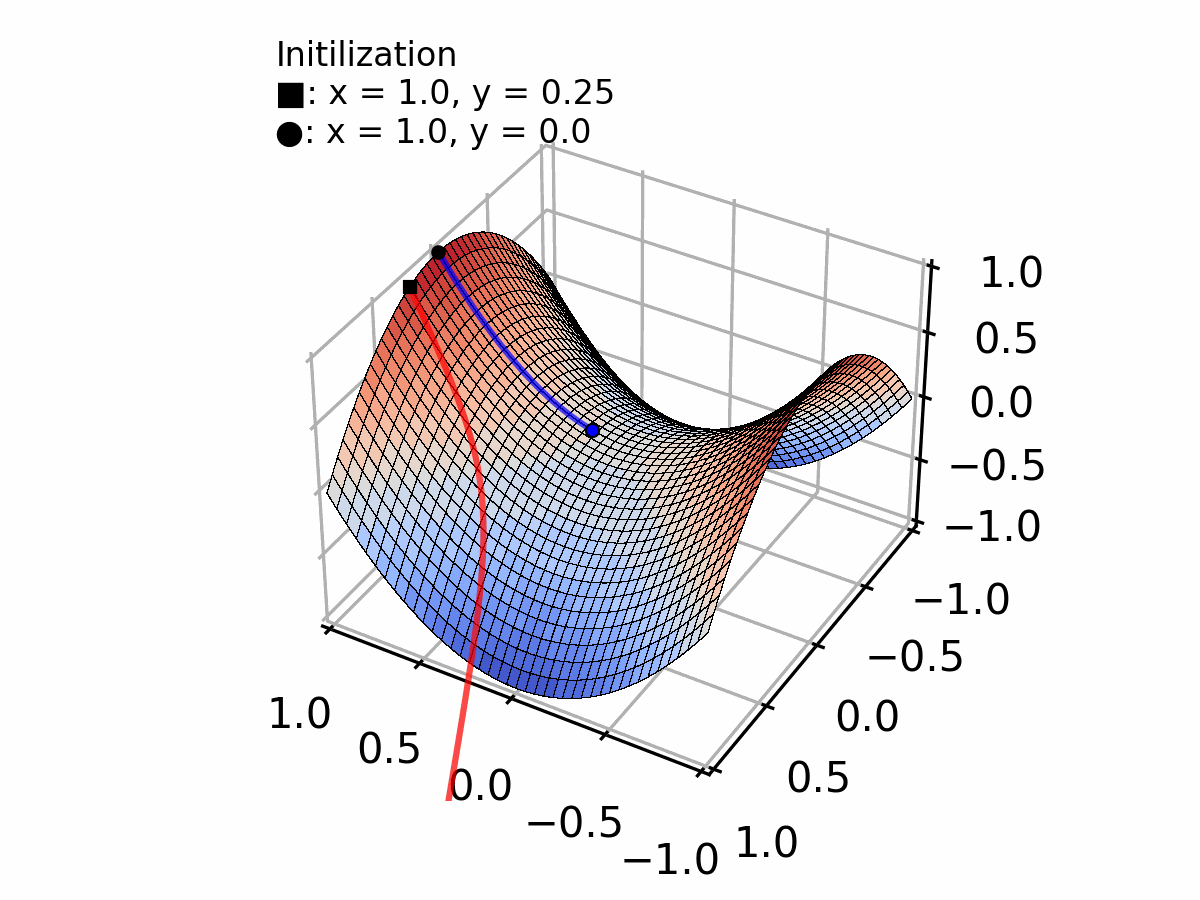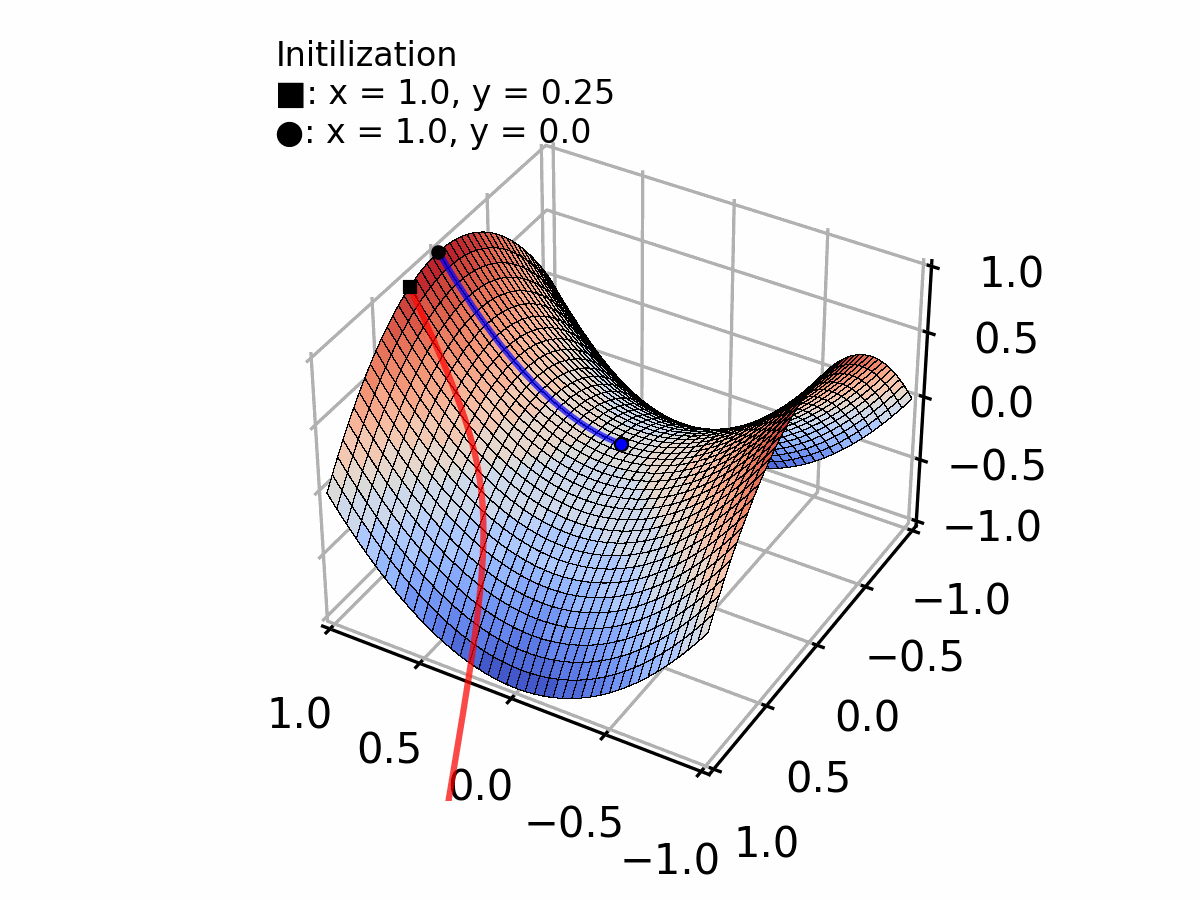
경사 하강법(GD)은 전체 훈련 데이터를 사용하여 경사를 따라 내려가면서 Weight를 업데이트하여 Global Minima를 찾는 방법이다.

 

여담으로 Vanila Gradient Descent라고도 불리는데 가장 Baisc 한 모델에 Valina라는 접두어를 붙이고는 한다. 이 Valina는 아이스크림의 기본맛이 바닐라 아이스크림이라서 이후에 "기본적인"이라는 의미로 다른 곳에도 쓰인다고 한다.

 

수식은 아래와 같다.

$$ \theta = \theta - \eta \nabla J(\theta) $$

 

GD는 직관적이고 전체 데이터를 이용하여 경사 하강을 진행하기 때문에 안정적인 수렴을 기대할 수 있다.

 

하지만 전체에서 가장 최소가 되는 부분인 Global Minima를 발견해하지 못하고 지역 최소값 또는 극솟값인 Local Minima에 빠지게 될 수 있다. 또한 모든 데이터를 이용하여 경사 하강법을 진행하는 것은 계산 효율성이 좋지 못하다.

 

Fig 5. Local Minima

 

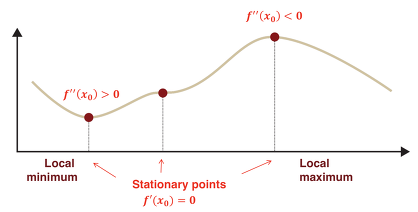
그림을 보면 Local minimum과 Local maximum을 정상점 및 2차 미분값을 통해 알 수 있다. 하지만 가운데 점은 최솟값인지 최댓값인지 구분하기가 어렵다. 이 부분을 안정점(Saddle Point)라고 부른다.

 

장점

• 직관적이고 간단한 이해: 구현이 쉬워 초보자도 쉽게 사용할 수 있다.
• 정확한 기울기 계산: 전체 데이터 사용으로 정확한 기울기를 제공한다.
• 안정적 수렴: 전체 데이터 기반으로 수렴이 비교적 안정적이다.

 

단점

• 계산 비용이 큼: 모든 데이터를 사용하므로 시간과 메모리 소모가 크다.
• 느린 수렴 속도: 업데이트가 느리며 대규모 데이터에서는 비효율적이다.
• 지역 최소값(Local Minima) 문제: 복잡한 경로에서 지역 최소값에 빠질 위험이 있다.

 

Stochastic Gradient Descent(SGD)

확률적 경사 하강법(SGD)은 GD가 모든 데이터를 이용하여 계산 효율성이 좋지 못한 점을 매 학습 단계에서 데이터셋의 한 샘플만 사용하여 기울기를 계산하고 매개변수를 업데이트하여 해결하였다.

 

SGD는 빠른 업데이트가 가능하므로 큰 데이터셋에서도 메모리 사용량을 줄이고 계산 속도를 높일 수 있다.

 

하지만 매번 샘플 하나로만 기울기를 계산하기 때문에 기울기 추정이 불안정하고 결국 GD와 같이 Local Minima에 빠질 확률이 여전히 높다.

 

수식은 아래와 같다.

$$ \theta = \theta - \eta \nabla_{\theta} J(\theta; x^{(i)}, y^{(i)}) $$

 

장점

• 빠른 업데이트: 매번 샘플 하나를 사용해 즉시 업데이트가 가능하므로 큰 데이터셋에서도 계산 속도가 빠르다.
• 저장 효율성: 전체 데이터셋을 필요로 하지 않으므로 메모리 사용량이 적다.
• Local Minima 탈출: 진동이 발생하기 때문에 지역 최적점에서 벗어나는 데 도움이 된다.

 

단점

• 기울기 불안정성: 샘플 하나만을 사용하여 기울기를 계산하므로 기울기 추정이 불안정하다.
• 수렴 속도 불안정: 흔들림 때문에 최적점 근처에서 안정적으로 수렴하지 못하고 진동이 발생한다.
• 학습률 조절 필요: 불안정한 수렴을 방지하기 위해 학습률을 조절하는 기술 필요하다.

 

Mini-Batch Gradient Descent(MGD) or Mini-Batch Stochastic Gradient Descent(MSGD)

Mini-Batch Gradient Descent는 GD, SGD의 중간이라 볼 수 있다. 전체나 하나의 데이터만 보는 것이 아니라 미니 배치(Mini Batch)를 통해 가중치를 업데이트 하는 방안을 제시하였다. 요즘은 이 MGD를 SGD로 혼용해서 많이 부르는 것 같다. 

 

훈련 데이터의 일부 샘플을 미니 배치(Mini Batch)로 만들어 기울기를 계산하고 가중치를 업데이트한다. 이는 전체 데이터(Batch)가 아닌 일부 데이터(Mini Batch)에서 계산하기 때문에 Global minima를 찾을 확률이 높다.

GD와 비교해서 속도가 빠르고 더 SGD 보다 더 안정적이지만 이 방법 역시 Local Minima 문제를 완전히 해결할 수는 없다.

 

수식은 아래와 같다.
$$ \theta = \theta - \eta \frac{1}{m} \sum_{i=1}^{m} \nabla_{\theta} J(\theta; x^{(i)}, y^{(i)}) $$

 

장점

• 균형 잡힌 효율성: 전체 데이터를 사용하지 않으므로 메모리 효율적이면서도 연산이 안정적이다.
• 수렴 속도 안정성: 배치 단위로 평균 기울기를 계산하므로 더 안정적인 수렴 가능하다.
• 병렬 연산 가능성: GPU 등의 병렬 연산을 이용해 속도와 효율성을 극대화 한다.

 

단점

• 추가 메모리 필요: 배치 크기가 커질수록 메모리 사용량이 증가한다.
• 배치 크기 조정 필요: 적절한 배치 크기를 찾기 위해 실험적인 조정 필요하다.
• 병렬 처리 지원 필수: GPU 등의 병렬 처리를 사용할 수 없는 경우 학습 속도가 저하될 수 있다.

 

Momentum

Momentum은 SGD에 물리의 운동량의 개념인 관성을 추가하여, 이전 업데이트의 방향(Momentum)과 현재 위치의 기울기를 고려해 가중치를 조정하는 방법이다.

 

하지만 Global Minima를 찾았는데도 계속 진행하여 과도한 업데이트를 유발할 가능성이 있다.

$$ v_t = \beta v_{t-1} + (1 - \beta) \nabla J(\theta) $$ $$ \theta = \theta - \eta v_t $$

 

장점

• 빠른 수렴: 이전의 기울기를 고려하여 빠르게 수렴한다.
• 진동 감소: 관성으로 인해 진동을 줄일 수 있다.
• 탐색 범위 확대: 이전 방향을 고려하여 탐색 범위를 넓힌다.

단점

• 하이퍼파라미터 조정 필요: 모멘텀 비율을 설정하는 것이 중요하지만 어려울 수 있다.
• 지속적인 업데이트 필요: 이전의 정보가 항상 반영되므로 최신 정보를 놓칠 수 있다.
• 메모리 소모: 이전 기울기를 저장해야 하므로 메모리 사용이 늘어난다.

 

Nesterov Accelerated Gradient (NAG)

NAG는 Momentum의 변형으로, 현재 위치를 기반으로 미리 한 발 앞으로 나가서 기울기를 계산하는 방법이다.

$$ v_t = \beta v_{t-1} + (1 - \beta) \nabla J(\theta - \beta v_{t-1}) $$

$$ \theta = \theta - \eta v_t $$

 

장점

• 미리 예측된 기울기 사용: 업데이트 전에 한 발 앞서가므로 수렴 속도가 빠르다.
• 진동 감소: 모멘텀을 기반으로 하여 진동을 줄인다.
• 정확한 기울기 계산: 현재 위치를 고려한 더 정확한 기울기를 제공한다.
  
  

단점

• 복잡한 구현: 기본 모멘텀보다 구현이 복잡하다.
• 하이퍼파라미터 조정: 적절한 하이퍼파라미터 조정이 필요하다.
• 과적합 가능성: 업데이트가 빠르기 때문에 과적합이 발생할 수 있다.

 

Adagrad

Adagrad는 각 매개변수에 대해 학습률을 적응적으로 조정하는 방식이다.

 

쉽게 말해 지금까지 비교적 훨씬 많이 업데이트된 변수는 적게, 적게 업데이트된 변수는 많이 업데이트하는 방법이다.

$$ G_t = \sum_{i=1}^{t} \nabla J(\theta^{(i)})^2 $$

$$ \theta = \theta - \frac{\eta}{\sqrt{G_t + \epsilon}} \nabla J(\theta) $$

 

장점

• 적응형 학습률: 각 매개변수에 대해 개별적으로 학습률을 조정하여 효율적이다.
• 드물게 발생하는 특징 학습: 드물게 나타나는 특성에 대한 학습이 용이하다.
  e.g.) 이미지 데이터셋에 대부분 고양이와 강아지 사진이 많지만 가끔 토끼 사진이 섞여 있을 때
• 간단한 구현: 특별한 튜닝 없이 기본 구현으로 효과를 볼 수 있다.

단점

• 학습률 감소 문제: 시간이 지남에 따라 학습률이 급격히 감소할 수 있다.
• 장기 학습에 비효율적: Epoch이 길어지면 학습률이 지나치게 낮아질 수 있다.
• 일반화 성능 저하: 고정된 학습률 감소로 인해 일반화 성능이 저하될 수 있다.

 

RMSprop

RMSprop은 Adagrad의 문제를 해결하기 위해 최근 기울기 제곱을 기반으로 학습률을 조정한다.

 

다시 말해 Adagrad는 지금까지 업데이트한 전체 총량을 고려해서 업데이트를 진행한다면, RMSProp는 최근에 업데이트한 양을 고려한다.

$$ G_t = \beta G_{t-1} + (1 - \beta) \nabla J(\theta)^2 $$

$$ \theta = \theta - \frac{\eta}{\sqrt{G_t + \epsilon}} \nabla J(\theta) $$

장점

• 효율적인 학습률 조정: 최근 기울기 제곱을 기반으로 하여 학습률을 조정한다.
• 빠른 수렴 속도: 학습률 감소 문제를 완화하여 효과적으로 수렴할 수 있다.
• 미니배치 학습에 적합: 대규모 데이터에서 잘 작동한다.

단점

• 하이퍼파라미터 조정 필요: 적절한 하이퍼파라미터 설정이 필요하다.
• 메모리 소모: 기울기 제곱의 평균을 저장하므로 메모리 사용량이 많다.
• 최적화가 어려움: 최적의 성능을 내기 위해 추가적인 조정이 필요할 수 있다.

 

Adam(Adaptive Moment Estimation)

Adam은 Momentum과 RMSprop의 장점을 결합하여, 각 매개변수의 기울기 평균과 제곱 기울기 평균을 기반으로 적응적인 학습률을 설정하는 방법이다. 가장 보편적으로 널리 쓰이는 옵티마이저이기도 하다.

$$ m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla J(\theta) $$ $$ v_t = \beta_2 v_{t-1} + (1 - \beta_2) \nabla J(\theta)^2 $$ $$ \hat{m}_t = \frac{m_t}{1 - \beta_1^t}  $$ $$ \hat{v}_t = \frac{v_t}{1 - \beta_2^t} $$ $$ \theta = \theta - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t $$

 

장점

• 빠른 수렴: 모멘텀과 RMSprop의 장점을 결합하여 일반적으로 빠른 수렴 속도를 제공한다.
• 적응형 학습률: 각 매개변수에 대해 적응적인 학습률을 제공하여 효율적이다.
• 사용자 친화적: 잘 작동하고 다양한 문제에 적용 가능하다.

 

단점

• 메모리 사용량 증가: 각 매개변수에 대해 추가적인 정보를 저장해야 하므로 메모리 사용량이 많다.
• 하이퍼파라미터 조정 필요: 몇 가지 하이퍼파라미터를 적절히 조정해야 최적 성능을 발휘할 수 있다.
• 과적합 위험: 모델이 복잡할 경우 과적합 위험이 있다.

 

AdaDelta

AdaDelta는 Adagrad의 아이디어를 발전시켜, 학습률이 감소하는 문제를 해결하는 방법이다.

$$ E[g^2]_t = \beta E[g^2]_{t-1} + (1 - \beta) g^2 $$ $$ \theta = \theta - \frac{g}{\sqrt{E[g^2]_t} + \epsilon} $$

 

장점

• 하이퍼파라미터 조정 불필요: 이전 기울기를 고려하므로 추가적인 하이퍼파라미터 조정이 필요 없다.
• 시간에 따라 적응: 각 매개변수의 특성에 맞춰 학습률을 조정한다.
• 안정적인 업데이트: 안정적인 가중치 업데이트가 가능하다.

 

단점

• 구현 복잡성: 기본 원리 이해가 어렵고 구현이 복잡할 수 있다.
• 기존 옵티마이저보다 느림: 일반적인 상황에서 다른 옵티마이저보다 느릴 수 있다.
• 비효율적 메모리 사용: 최근 기울기와 이전 기울기를 저장해야 하므로 메모리 사용량이 증가한다.

 

FTRL(Follow The Regularized Leader)

FTRL은 주로 온라인 학습에 사용되며, 정규화된 리더의 접근 방식을 기반으로 한 방법이다.

$$ \theta_t = \arg \min_{\theta} \left( \sum_{i=1}^t J(y_i, f(x_i; \theta)) + \lambda R(\theta) \right) $$

 

장점

• 온라인 학습에 적합: 실시간 데이터에 잘 대응하여 효율적인 학습이 가능하다.
• 정규화 사용: 과적합을 방지하기 위한 정규화를 쉽게 적용할 수 있다.
• 다양한 응용 가능성: 다양한 문제에 적용할 수 있는 유연성이 있다.

 

단점

• 구현 난이도: 업데이트 규칙이 복잡하여 구현이 어렵다.
• 대규모 데이터 처리의 어려움: 큰 데이터 세트에서 처리 속도가 느려질 수 있다.
• 메모리 소모: 각 매개변수에 대한 정보를 저장해야 하므로 메모리 사용량이 많다.

 

아래는 python을 이용하여 GD와 Adam의 가중치 업데이트 과정을 표현한 소스 코드이다.

 

import numpy as np
import tensorflow as tf

# 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 1) * 10  # 0부터 10 사이의 랜덤한 x 값
y = 2 * X + 1 + np.random.randn(100, 1)  # y = 2x + 1에 노이즈 추가

# 단순 경사하강법
learning_rate = 0.01
num_iterations = 1000
m = 0.0  # 기울기 초기값
b = 0.0  # 절편 초기값

for _ in range(num_iterations):
    y_pred = m * X + b
    error = y_pred - y
    m_gradient = (2 / len(X)) * np.dot(X.T, error)
    b_gradient = (2 / len(X)) * np.sum(error)
    m -= learning_rate * m_gradient
    b -= learning_rate * b_gradient

# Adam 옵티마이저
model = tf.keras.Sequential([
    tf.keras.layers.Dense(1, input_shape=(1,))
])
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X, y, epochs=1000, verbose=0)

weights = model.layers[0].get_weights()
m_adam = weights[0][0][0]  # 기울기
b_adam = weights[1][0]  # 절편

# 결과 출력
print(f"단순 경사하강법 - 기울기: {m}, 절편: {b}")
print(f"Adam 옵티마이저 - 기울기: {m_adam}, 절편: {b_adam}")

# 단순 경사하강법 - 기울기: [[1.99437925]], 절편: 1.2177417283305512
# Adam 옵티마이저 - 기울기: 2.0278589725494385, 절편: 1.009575605392456

 

관련 포스트

2024.10.27 - [Data Science/ML & DL] - 활성화 함수(Activation Function) - Sigmoid, Softmax, Tanh, ReLU, Leaky ReLU

 

2024.10.26 - [Data Science/ML & DL] - 손실 함수(Loss Function)와 모델 유형 및 분야 별 적용 방법

 

---

 

참고 자료

 

https://velog.io/@chang0517/Optimizer-%EC%A2%85%EB%A5%98-%EB%B0%8F-%EC%A0%95%EB%A6%AC

 

https://hwiyong.tistory.com/9

 

https://medium.com/data-science-365/overview-of-a-neural-networks-learning-process-61690a502fa

 

https://towardsdatascience.com/creating-a-gradient-descent-animation-in-python-3c4dcd20ca51

 

https://smcho1201.tistory.com/3

 

https://www.youtube.com/watch?v=mccscAH2kkk