Perplexity(PPL)란 텍스트 생성(Text Generation) 언어 모델의 성능 평가지표 중 하나이다. Perplexity는 단어의 사전적 의미를 고려하여 설명하자면 모델이 예측을 할 때 얼마나 "당황"하거나 "혼란"을 겪는지를 측정하는 것이다. 이는 모델에 따른 테스트 세트의 엔트로피(또는 평균 로그 가능도, average log-likelihood)의 지수로 계산된다. 일반적으로 테스트 데이터셋이 충분히 신뢰할 만할 때 Perplexity 값이 낮을수록 언어 모델이 우수하다고 평가한다. 더 나아가 Perplexity는 자연어 모델에서 손실 함수로도 사용될 수 있다. 수학적으로는 Cross-Entropy Loss의 지수 함수와 같은 형태를 보인다.
수식은 아래와 같다.
$$ P(W) = \sqrt[N]{\frac{1}{P(w_1, w_2, \dots, w_N)}} $$
로그 확률을 사용할 경우는 아래와 같다.
$$ P(W) = 2^{-\frac{1}{N} \sum_{i=1}^N \log_2 P(w_i)} $$
- \( W = w_1, w_2, \dots, w_N \): 단어 시퀀스
- \( N \): 시퀀스의 단어 수
- \( P(w_i) \): 모델이 예측한 각 단어 \( w_i \)의 확률
예를 들어 어떤 언어 모델이 다음과 같은 3개의 단어 시퀀스를 예측한다고 가정해 보자.
- 시퀀스(Sequence): "I love machine learning"
- 모델의 각 단어 예측 확률
- \( P(I) = 0.5 \)
- \( P(love) = 0.2 \)
- \( P(machine) = 0.05 \)
- \( P(learning) = 0.1 \)
이 시퀀스의 perplexity \( P(W) \)를 구하는 과정은 다음과 같다.
- 각 단어 확률의 곱으로 전체 시퀀스 확률을 계산
$$ P(W) = P(I) \times P(love) \times P(machine) \times P(learning) = 0.5 \times 0.2 \times 0.05 \times 0.1 = 0.0005 $$ - Perplexity 계산
: 전체 시퀀스의 perplexity는 다음과 같이 구할 수 있다.
$$ \text{Perplexity} = \sqrt[4]{\frac{1}{P(W)}} = \sqrt[4]{\frac{1}{0.0005}} \approx 11.18 $$
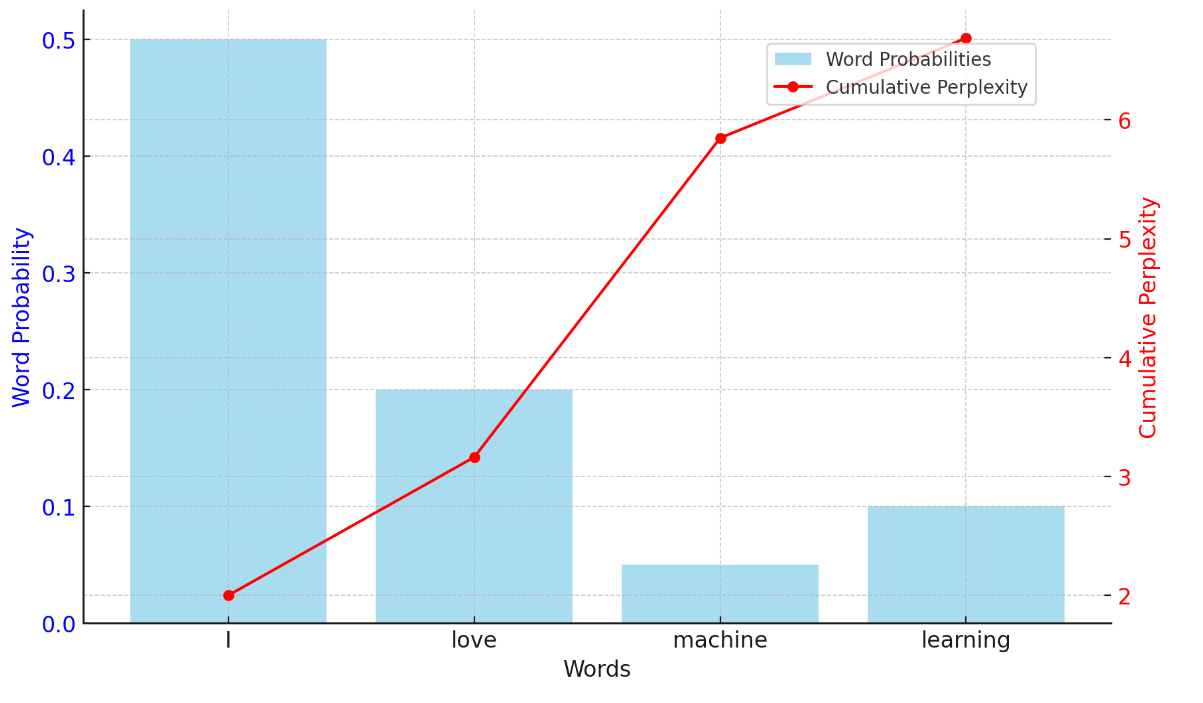
따라서 이 모델의 perplexity는 약 11.18이 된다. 이 값은 모델이 이 시퀀스를 얼마나 "혼란스럽게" 예측하고 있는지 나타낸다. Perplexity 값이 낮을수록 모델이 시퀀스를 더 잘 예측하고 있음을 의미한다.
참고로 언어 모델에서 단어 시퀀스에 대해 Perplexity를 계산할 때, 각 단어의 예측 확률은 독립적으로 계산되므로 합이 1이 될 필요는 없다. 다만 모델이 특정 조건에서 다음 단어를 예측하는 확률을 제공할 때는 모든 가능한 단어에 대한 확률의 합이 1이 되어야 한다. 예를 들어, 한 문장에서 다음에 올 단어를 예측할 때는 해당 문맥에서 가능한 단어들의 확률 분포로 제공된다. 아래와 같은 경우이다.
예시) "The cat sat on the ___"
: {"mat": 0.6, "hat": 0.1, "water": 0.1, "sofa": 0.2}
즉, Perplexity 계산에 사용된 확률들은 모델의 단어 예측이 독립적이며, 문맥에 따른 조건부 확률이 아닌 경우라면 합이 1이 되지 않아도 문제가 없다.
마지막으로 Perplexity 평가 방법에 있어서 주의할 점은 PPL의 값이 낮다는 것은 테스트 데이터 상에서 높은 정확도를 보인다는 것이지, 사람이 직접 느끼기에 좋은 언어 모델이라는 것을 반드시 의미하진 않는다. 또한 언어 모델의 PPL은 테스트 데이터에 의존하므로 두 개 이상의 언어 모델을 비교할 때는 정량적으로 양이 많고, 또한 도메인에 알맞은 동일한 테스트 데이터를 사용해야 신뢰도가 높아진다.
참고 자료
https://heytech.tistory.com/344
https://rfriend.tistory.com/851

