Softmax와 볼츠만 분포(Boltzmann Distribution)
Softmax는 최근 딥러닝 모델 연구에서 아주 중요한 역할을 한다. 대표적으로 GPT의 근간이 되는 Transformer 모델과 Attention 메커니즘에서 매우 중요한 역할을 수행하고 있다.
Softmax는 주로 다중 클래스 분류 문제에서 사용되며, 입력된 로짓(logits)을 기반으로 각 클래스에 대한 확률을 계산하는 데 활용된다. 여러 카테고리 간의 확률 분포를 부드럽게 만들어 주는 역할을 한다. 이 글에서는 Softmax의 특징과 이를 개선하기 위한 다양한 기법에 대해 정리해보려 한다.
Softmax는 볼츠만 분포(Boltzmann Distribution)에 영감을 받아 고안되었다.
여기서 볼츠만 분포란 열역학적 시스템의 입자들이 에너지를 어떻게 분포하는지를 설명하는 중요한 도구로, 온도와 에너지 상태에 따라 입자가 특정 에너지를 가질 확률을 정량적으로 나타내는 분포이다. Softmax와 비교해 보며 아래 수식을 살펴보자.
$$ boltzmann = P(E_i) = \frac{e^{-E_i / (kT)}}{\sum_j e^{-E_j / (kT)}} = \frac{e^{Q(i) / \tau}}{\sum_{j=1}^N e^{Q(j) / \tau}} $$
$$ \text{softmax}(z_i) = \frac{\exp(z_i)}{\sum_{j=1}^{K} \exp(z_j)} $$
어려우니 볼츠만 분포에 관련된 한 가지 예시를 보고 넘어가자.
뜨거운(=temperature, \( \tau \)) 커피를 컵에 담고 식힐 때, 커피의 분자들은 높은 에너지(=엔트로피)를 가지고 있다. 시간이 지나면서 커피의 온도가 낮아지는데, 이 과정에서 일부 분자들이 에너지를 잃고 낮은 에너지 상태로 이동한다. 이때 커피의 온도가 주변 공기와 비슷해지면서 분자들의 에너지 분포가 변화하게 된다.
이 내용을 Softmax로 가져와보자.
위 예시에서 온도 파라미터(\( \tau \))는 확률 분포의 부드러움(스무딩)과 관련이 있다. 온도가 높으면 Softmax 출력이 여러 값에 고르게 분포되지만, 온도를 낮추면 특정한 클래스에 집중되며 출력이 균등하지 않게 된다.
아래는 Softmax와 볼츠만 분포를 python으로 구현한 소스 코드이다.
def softmax(z):
e_z = np.exp(z - np.max(z))
return e_z / e_z.sum()
def boltzmann(z, temperature):
exponent = np.true_divide(z - np.max(z), temperature)
return np.exp(exponent) / np.sum(np.exp(exponent))
logits = [1, 2, 3]
tmp = 10 # or 1
softmax(logits)
boltzmann(logits, tmp)
# tmp = 1
# [0.09003057 0.24472847 0.66524096]
# tmp = 10
# [0.30060961 0.33222499 0.3671654 ]
각 함수들에서 최댓값을 모든 가중치에서 빼고 시작하는데 이는 지수가 커서 발생하는 부작용을 줄이기 위함이다. 오버플로우를 방지하기 위함이라고 봐도 좋다. 아래 계산 효율성 개선 부분과 연관되어 있다.
온도(tmp) 변수가 1 일 때보다 10일 때 더 출력이 균등해진 것을 확인할 수 있다. 개인적으로 내용이 어려워 자세히 알지는 못하고 있으니 대충 내용만 알고 넘어가자.
다시 Softmax로 돌아와 수식을 좀 더 자세히 살펴보자.
$$ \text{softmax}(z_i) = \frac{\exp(z_i)}{\sum_{j=1}^{K} \exp(z_j)} $$
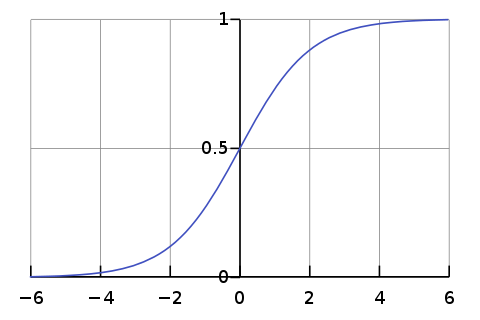
여기서 \( z_i \)는 각 클래스의 로짓(logit) 값이며, \( K \)는 전체 클래스의 수이다. Softmax 함수는 모든 클래스의 확률이 합이 1이 되도록 하여 모델이 예측한 확률적 해석을 가능하게 한다.
로짓(Logit)이란?
Softmax에서 로짓(logit)은 모델이 각 클래스에 대해 예측한 값으로, Softmax 함수의 입력으로 사용된다. 로짓은 모델의 신뢰도를 나타내며, 높은 로짓 값은 해당 클래스에 대한 강한 확신을 의미한다.
로짓은 모델이 특정 클래스를 얼마나 잘 예측하고 있는지를 나타내는 원시 점수(raw score) 또는 예측 값이다. 이 값은 보통 신경망의 마지막 층에서 계산되며, 각 클래스에 대해 하나씩 존재한다.
예를 들어, 이미지 분류 모델이 고양이, 개, 토끼라는 세 가지 클래스를 예측한다고 가정하자. 모델의 출력은 다음과 같은 로짓 값으로 표현될 수 있다:
- 고양이: \( z_{cat} \) = 2.0
- 개: \( z_{dog} \) = 1.0
- 토끼: \( z_{rabbit} \) = 0.5
여기서 각 로짓 값은 해당 클래스의 예측 점수를 나타낸다. 더 높은 로짓 값은 해당 클래스가 선택될 가능성이 높다는 것을 의미한다.
- 고양이일 확률
$$ P(\text{cat}) = \frac{e^{2.0}}{e^{2.0} + e^{1.0} + e^{0.5}} \approx \frac{7.39}{7.39 + 2.72 + 1.65} \approx \frac{7.39}{11.76} \approx 0.63 $$
- 개일 확률
$$ P(\text{dog}) = \frac{e^{1.0}}{e^{2.0} + e^{1.0} + e^{0.5}} \approx \frac{2.72}{11.76} \approx 0.23 $$
- 토끼일 확률
$$ P(\text{rabbit}) = \frac{e^{0.5}}{e^{2.0} + e^{1.0} + e^{0.5}} \approx \frac{1.65}{11.76} \approx 0.14 $$
위 결과에 따라 고양이, 개, 토끼일 확률이 아래와 같이 결정되게 된다.
- 고양이: 63%
- 개: 23%
- 토끼: 14%
위와 같이, 로짓 값이 각 클래스의 확률로 변환되는 과정을 통해 Softmax의 역할을 이해할 수 있다.
분류 카테고리 수가 많을 경우
이러한 Softmax는 분류 카테고리 수가 증가하게 되면 클래스 간 불균형 문제가 발생하게 된다. 그러므로 클래스가 너무 적거나 많을 경우, 모델의 예측 성능이 저하될 수 있다. 또한 카테고리가 많아질수록 모델이 복잡해지며, 이는 학습 과정에서 과적합(Overfitting)을 초래할 수 있다.
문제를 해결하기 위한 방안으로는 다음과 같은 기법들이 사용된다.
- 정규화 기법: L2 정규화나 Dropout과 같은 기법을 적용하여 과적합을 방지한다.
- 클래스 간 불균형 처리: 오버샘플링이나 언더샘플링 기법을 통해 클래스의 분포를 조정한다.
- 서브셋 학습: 데이터셋을 서브셋으로 나누어 학습하여, 모델이 다양한 클래스에 고루 노출될 수 있도록 한다.
- 어텐션 메커니즘 사용: Attention 메커니즘을 통해 중요도가 높은 특징에 집중할 수 있다.
이외에도 Bias를 조절하여 해결할 수도 있다.
Bias를 이용한 클래스 불균형 해결
Softmax의 Bias 조절은 모델의 출력 확률 분포에 영향을 미치는 중요한 요소이다. 여기서 Bias는 Softmax 함수에 입력되는 로짓(logit) 값에 추가되는 상수 값으로, 이를 통해 특정 클래스의 확률을 높이거나 낮출 수 있다.
Bias를 조절하는 것은 Softmax에 들어가는 로짓 값에 직접 영향을 미친다. Bias를 더하거나 빼면 특정 클래스의 로짓 값을 인위적으로 변경할 수 있어, 그 클래스의 출력 확률을 조절할 수 있다. Bias는 보통 실수 값으로 설정되며, 특정 클래스에 대해 다음과 같이 설정할 수 있다.
- Positive Bias: 특정 클래스의 로짓에 양수를 더하면, 그 클래스의 확률이 증가한다. 즉, 해당 클래스가 선택될 가능성이 높아진다.
- Negative Bias: 특정 클래스의 로짓에 음수를 더하면, 그 클래스의 확률이 감소한다. 즉, 해당 클래스가 선택될 가능성이 낮아진다.
위 Logit의 예시를 다시 가지고 와 예를 들어보자. 이번엔 '개' 클래스에 대해 +1의 Bias를 추가하였다.
- 고양이: \( z_{cat} \) = 2.0
- 개: \( z_{dog} \) = 1.0 + 1.0(Bias)
- 토끼: \( z_{rabbit} \) = 0.5
이제 다시 이 확률을 Softmax에 대입해 보면 아래와 같다.
- 고양이일 확률
$$ P(\text{cat}) = \frac{e^{2.0}}{e^{2.0} + e^{2.0} + e^{0.5}} \approx \frac{7.39}{7.39 + 7.39 + 1.65} \approx \frac{7.39}{16.42} \approx 0.45 $$
- 개일 확률
$$ P(\text{dog}) = \frac{e^{2.0}}{e^{2.0} + e^{2.0} + e^{0.5}} \approx 0.45 $$
- 토끼일 확률
$$ P(\text{rabbit}) = \frac{e^{0.5}}{e^{2.0} + e^{2.0} + e^{0.5}} \approx \frac{1.65}{16.42} \approx 0.1 $$
여기서 '개'의 확률이 상승하고, '고양이'와 '토끼'의 확률은 상대적으로 줄어들게 된다.
기울기 소멸 문제 해결(Log Softmax)
Softmax는 기울기 소멸 문제(vanishing gradient problem)에 취약하기 때문에 Log를 활용하여 이 문제를 보완할 수 있다.
만약 Softmax 수식에 x가 1000이라면 \( e^{1000} \)이 되고 오버플로우를 유발할 수 있다. Log를 사용함으로써 이 부분에 대해 수치적 안정성을 부여할 수 있다.
또한 이 Log를 활용하면 곱셈과 나눗셈 연산을 덧셈과 뺄셈으로 변환하여 계산 효율성을 개선할 수 있다. 이는 로그-합-지수(log-sum-exp) 트릭으로 알려져 있으며, 계산을 수행할 때 수치적으로 더 안정적인 결과를 얻을 수 있는 이점을 제공한다.
$$ \text{Log-Softmax}(x_i) = log( \frac{e^{x_i}}{\sum_{j} e^{x_j}} ) = x_i - \log\left(\sum_{j} e^{x_j}\right) $$
아래는 python으로 구현한 소스 코드이다.
import numpy as np
def log_softmax1(z):
e_z = np.exp(z - np.max(z))
return np.log(e_z / e_z.sum())
def log_softmax2(z):
return z - np.max(z) - np.log(np.sum(np.exp(z - np.max(z))))
logits = np.array([2.0, 1.0, 0.1])
print(log_softmax1(logits))
print(log_softmax2(logits))
두 함수의 결과값은 동일하다. log_softmax2 함수는 계산이 좀 더 단순해진 것을 보여주기 위해 구현하였다.
참고로 이 코드는 수치적 안정성을 위해 로짓에서 최댓값을 빼는 방식까지 포함하였다. 이런 방식으로 Softmax를 구하게 된다면 수식은 아래와 같다.
$$ \text{Softmax}(x_i) = \frac{e^{x_i - M}}{\sum_{j} e^{x_j - M}} $$
이렇게 최대값을 빼줘도 출력 확률 분포는 동일하며 오버플로우 문제를 방지할 수 있다.
최댓값을 뺀 Log Softmax는 아래와 같이 표현 가능하다.
$$ \text{Log-Softmax}(x_i) = x_i - \max(x) - \log\left(\sum_{j} e^{x_j - \max(x)}\right) $$
연속 확률 분포에의 적용
Softmax를 연속 확률 분포에 적용하면 예측할 연속 변수를 범주화하여 보다 쉽게 이해하고 확률적 해석을 할 수 있다. 예를 들어 연속적인 값을 이산적으로 나누어 각 구간에 대한 확률을 계산함으로써 모델이 특정 범위에 해당하는 값이 나올 확률을 명확히 파악할 수 있다.
하지만 명확하게 아래와 같은 단점들도 존재한다.
- 이산성과 연속성의 불일치: 연속 확률 분포는 특정 값에 대한 확률을 0으로 가지기 때문에 Softmax의 이산적 성질과 충돌할 수 있다.
- 경계 문제: 연속 확률 분포를 다룰 때 Softmax를 사용하면 클래스가 서로 겹치지 않도록 하는 것이 어려울 수 있다. 연속적인 값은 특정한 경계가 없기 때문에, Softmax의 출력을 고정된 카테고리에 강제하는 것이 불가능하다. 이로 인해 모델의 유연성이 감소할 수 있다.
- 모델 해석의 어려움: Softmax의 출력을 연속적인 값으로 해석하는 것은 직관적이지 않을 수 있다. 연속 확률 분포에서 실제로 예측하는 것은 확률 밀도 함수이기 때문에, Softmax의 출력을 이러한 맥락에서 이해하고 해석하기가 어렵다.
- 스케일링 이슈: Softmax 함수는 입력 값의 스케일에 매우 민감하다. 연속적인 값을 입력으로 사용하면, 로짓(logit) 값의 변화가 결과 확률에 큰 영향을 미칠 수 있다.
- 기울기 소실(Gradient Vanishing): 연속적인 변수를 다룰 때 입력 값이 매우 큰 경우 기울기가 거의 0에 가까워져서 학습이 원활하게 진행되지 않을 수 있다.
관련 포스팅
참고 자료
https://thebook.io/080289/0281/
https://medium.com/@AbhiramiVS/softmax-vs-logsoftmax-eb94254445a2
https://velog.io/@kms39273/Actvation-function-softmax-logsoftmax-%EB%B9%84%EA%B5%90

