상관도표(Correlogram)는 시계열 데이터를 분석에서 자주 활용되는데 자기상관함수(Autocorrelation Function, ACF) 또는 편자기상관함수(Partial Autocorrelation Function, PACF)를 그래프로 표현한 것을 뜻한다. 우리가 자주 말하는 Correlation은 두 변수 간의 관계를 -1~1 사이로 정규화한 값으로 표현하는 척도인데, Autocorrelation은 time shifted된 자기 자신의 데이터와의 상관성을 의미한다.
이 ACF와 PACF는 ARIMA 모델의 파라미터가 되는 p, d, q의 최적 차수를 탐색할 때 유용하게 사용된다. p는 AR, d는 차분 횟수, q는 MA와 관련이 있는 파라미터이다. ACF와 PACF 설명 이전에 자기회귀 모형(Autoregressive model, AR)과 이동평균 모형(Moving Average model, MA)의 간단한 설명이 필요하다.
우선 AR은 p시점 이전 자료가 현재 자료에 영향을 주는 모형을 의미하는데 예를 들어 비가 안 오면 매출이 100만원이 될 수 있었는데 갑자기 폭우가 내려 매출의 범위가 80~120만원 정도로 변할 수 있다 추정하는 것이다.
MA는 과거의 어떠한 충격(shock)이 겹쳐 현재의 데이터에 영향을 끼친다는 것을 기반으로 만들어진 모형인데 예를 들면 월드컵 축구 경기(shock에 해당) 당일 치킨집 손님이 늘어나는 반면, 축구 경기를 보며 치킨을 많은 사람들이 먹었기 때문에 질려서 며칠간 치킨 주문이 감소하고 이러한 여파가 3일간 이어졌다면 MA(3) 모델을 이용해 주문량을 예측해볼 수 있다. 이러한 AR과 MA의 모델을 섞어서 이용하는 것이 ARIMA이다. AR, MA, ARIMA에 대해 조금 더 자세한 설명은 여기를 참조하길 바란다.
ACF(Autocorrelation function)
ACF는 k시간 단위로 구분된 시계열 관측치 간의 \( y_t \)와 \( y_{t+k} \)간 상관 관계를 측정하는 것이다. ACF의 반환값의 절대값이 커질수록 시차 시계열 데이터의 상관성이 크다고 할 수 있다. 이 크다는 것의 기준은 p-value와 같이 95% 근사 신뢰구간으로 정할 수 있다. 또는 \( \pm 1.96 * {SE_k \over \sqrt{n}} \)를 신뢰구간으로 적용할 수 있는데 이때, \( SE_k = \sqrt{1+2\Sigma^{k}_{j=1} \vert{\hat{\gamma^{2}_j}}}\vert \)이다.
ACF는 정상성 데이터에 대해서는 0으로 빠르게 떨어지고 비정상성 데이터에는 천천히 수치가 떨어진다.
시차(lag)에 대한 ACF수식과 python 코드로 구현한 내용은 아래와 같다.
$$ \mathrm{ACF}(k) = \frac{\mathrm{cov}(y_t, y_{t+k})}{\mathrm{var}(y_t)} = \frac{\sum_{t=1}^{N-k}(y_t - \bar{y})(y_{t+k} - \bar{y})}{\sum_{t=1}^{N}(y_t - \bar{y})^2} \frac{N}{N - k}, \quad k = 0, 1, \ldots, N-1 $$
def acf(data, k):
data = np.array(data).reshape(-1)
mean = data.mean()
numerator = np.sum((data[:len(data)-k] - mean) * (data[k:] - mean))
denominator = np.sum(np.square(data - mean))
acf_val = numerator / denominator
return acf_val
# [1.0, 0.1048904805897309, -0.0021663171476797435, 0.025054864781747933, -0.016516709724606914,
# -0.038303324302299956, -0.025356924583006032, 0.005668275317742138, -0.03779181516554617,
# -0.03389716988734305, -0.04605595433803343, 0.09043427594152544, -0.04105851291659383,
# -0.03529945852644305, 0.03141655496394635, 0.030499542062679394]
PACF(Partial Autocorrelation function)
PACF는 ACF가 모든 시계열 데이터의 특성을 분석하는 것에 한계가 있기에 추가적인 분석의 필요에 따라 사용된다. 예를 들어 \( Y_t \)와 \( Y_{t-1} \)이 관계가 있다면 \( Y_{t-1} \)와 \( Y_{t-2} \)도 상관이 있고 \( Y_t \)와 \( Y_{t-2} \)는 \( Y_t \)와 \( Y_{t-1} \)간의 유의미한 관계가 있음으로 인해 상관있다는 결과가 도출될 수 있다는 점이다. 이 추가적인 분석에선 부분 상관이란 확률 변수인 X와 Y에 의해 모든 변수들에 대한 상관 관계를 분석한 후에도 아직 남아있는 상관관계를 해석한다. PACF는 \( y_t \)와 \( y_{t+k} \)간 상관 관계를 도출하는 것은 같지만 \( t \)와 \( t+k \) 간 다른 \( y \)값의 영향력은 배제하고 측정하는 방식이다. 즉 시차 \( k \)에서의 \( k \)단계만큼 떨어져 있는 모든 데이터들 간의 상관 관계를 말한다.
PACF가 시차 n에서 떨어지는 경우 AR(n)을 사용하고 하락이 점진적이라면 MA를 사용한다.
아래는 PACF 수식과 python 코드로 구현한 내용이다.
$$ PACF(k) = Corr(e_t, e_{t-k}) $$
def pacf(data, k):
if k == 0:
pacf_val = 1
else:
gamma_array = np.array([acf(data, k) for k in range(1, k + 1)])
gamma_matrix = []
for i in range(k):
temp = [0] * k
temp[i:] = [acf(data, j) for j in range(k - i)] # making diagonal
gamma_matrix.append(temp)
gamma_matrix = np.array(gamma_matrix)
gamma_matrix = gamma_matrix + gamma_matrix.T - np.diag(gamma_matrix.diagonal()) # making symmetric matrix
pacf_val = np.linalg.inv(gamma_matrix).dot(gamma_array)[-1]
return pacf_val
# [1, 0.1048904805897309, -0.013314819886420286, 0.026983316042088503, -0.022319613136047224,
# -0.034135621611999685, -0.018973200676100765, 0.01077296815748313, -0.038891688902602854,
# -0.026112882712660834, -0.04370773093454674, 0.10176785721931482, -0.06372947341414463,
# -0.02323371317763752, 0.026877099274573275, 0.027397356076868686]
# 해당 코드와 PACF의 수식에 대한 더 자세한 사항은 아래 블로그 참조
# => https://zephyrus1111.tistory.com/135
여기서 \( e_t=Y_t-(\beta_1Y_{t-1}+ ... +\beta_1Y_{t-(k-1)}) \)로 표현할 수 있다. 이는 \( e_t \)는 \( Y_{t-k} \)로 설명될 수 있는 부분을 제거한 것이고, \( e_{t-k} \) 또한 그러하다. 즉, PACF로 계산한다는 것은 부분적으로 \( y_t \)와 \( y_{t+k} \)의 상관관계만을 보겠다는 의미로 해석할 수 있다.

이제 python을 이용하여 ACF와 PACF를 구현해 시각화시켜 확인해본다.
시계열 데이터가 AR의 특성을 띄는 경우, ACF는 천천히 감소하고 PACF는 처음 시차를 제외하고 급격히 감소한다.
반면 MA의 특성을 띄는 경우 ACF는 급격히 감소하고 PACF는 천천히 감소한다.
예를 들어 ACF는 시차 1 이후 0에 가까워지고 PACF는 시차 2 이후 0에 수렴한다면 ACF, PACF 모두 점진적으로 0에 이르고 있는 것이고 따라서 AR(2), MA(1), ARMA(2, 1)등의 모델에 사용할 수 있다.
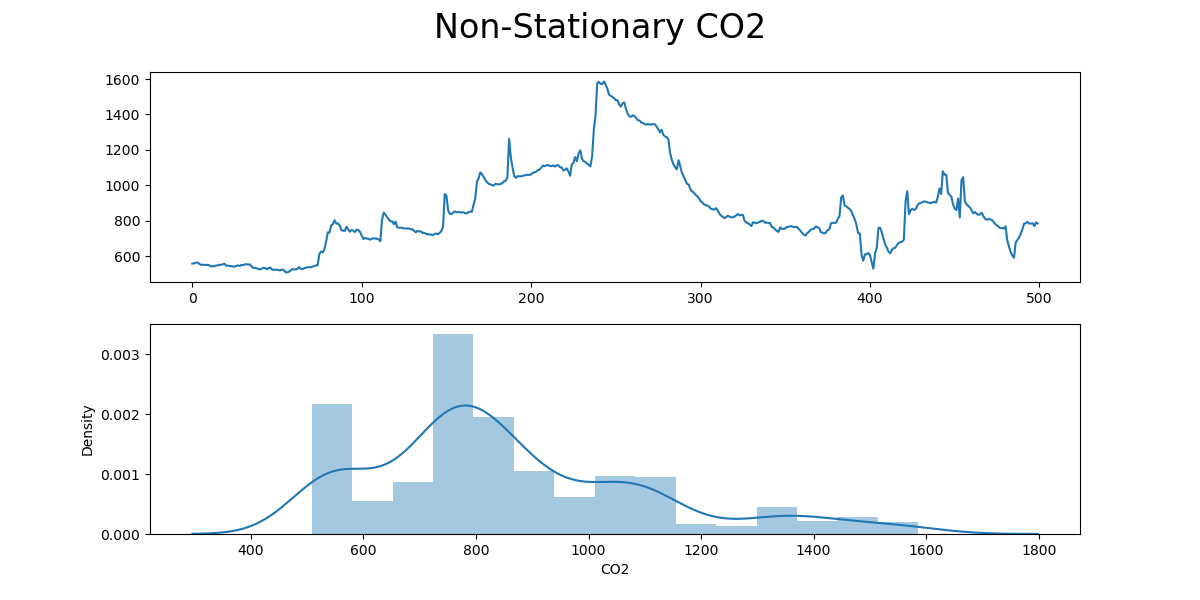
우선 1차 차분을 하지 않고 유동인구에 따라 영향을 받는 실내 이산화탄소 수치 비정상성 시계열 데이터의 원본이다.
또한 ACF, PACF의 lag은 15로 고정하고 아래 산출물들을 만들었다. lag은 15이지만 0까지 포함되어 반환되는 값은 16개가 된다.
아래는 비정상성 데이터의 ACF의 상관도표이다.
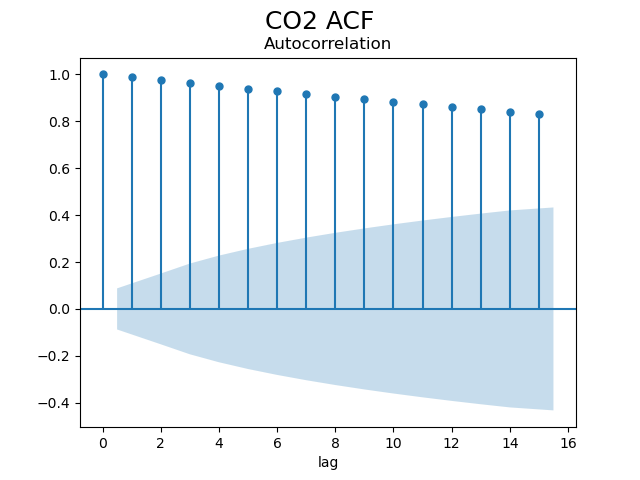
[1. 0.98944881 0.97703192 0.96464115 0.95184396
0.93927612 0.92732408 0.91585773 0.90425712
0.89331789 0.88292446 0.87327318 0.86187431
0.85118844 0.84109996 0.8302833 ]
lag은 위와 같이 산출되었다.
아래는 비정상성 데이터의 PACF의 상관도표이다.

[ 1. 0.98944881 -0.09418442 0.00281093
-0.02676177 0.00801682 0.0206311 0.01270599
-0.01631433 0.02648605 0.01444585 0.02808179
-0.09567857 0.04444847 0.0145546 -0.03780636]
이번에 lag은 위와 같이 산출되었다.
위 상관도표들에서 lag의 0 지점은 자기 자신과의 관계이므로 당연히 1이 나온다. 따라서 해석할 때 생략해도 무관하다. 절단점이란 어느 지점부터 파란 구간 안으로 데이터가 포함되는지를 말하는 지점이다. 현재 ACF 그래프에선 모든 데이터 간 상관관계가 크다고 나오며 점진적으로 감소하고, PACF에선 급격히 감소하여 절단점이 3(=lag)이 된다. 따라서 lag-1인 AR(2) 모델을 이용하면 비교적 좋은 결과를 얻을 수 있다고 추측할 수 있다.
이번엔 비정상성 데이터를 1차 차분을 통해 정상성 데이터로 변형한 후 상관도표를 그려본다.

어느 정도 정상성을 띄는 것 같다. p-value에 대한 분석은 생략한다.
아래는 정상성 데이터의 ACF의 상관도표이다.

[ 1. 0.10489048 -0.00216632 0.02505486
-0.01651671 -0.03830332 -0.02535692 0.00566828
-0.03779182 -0.03389717 -0.04605595 0.09043428
-0.04105851 -0.03529946 0.03141655 0.03049954]
정상성 데이터를 ACF에 넣어 얻은 lag은 위와 같이 산출되었다. 아까보다 상관관계가 약해진 것을 확인할 수 있고 절단점은 2가 된다.

[ 1. 0.10489048 -0.01331482 0.02698332 -0.02231961
-0.03413562 -0.0189732 0.01077297 -0.03889169
-0.02611288 -0.04370773 0.10176786 -0.06372947
-0.02323371 0.0268771 0.02739736]
lag은 위와 같이 산출되었다. 아까보다 상관관계가 약해진 것을 확인할 수 있고 절단점은 2가 된다. 따라서 해당 데이터는 ARMA(1, 1) 또는 원본 데이터를 차분하지 않고 사용한다면 ARIMA(1, 1, 1) 모델을 활용할 수 있다.
아래는 전체 python 소스 코드이다.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
def acf(data, k):
data = np.array(data).reshape(-1)
mean = data.mean()
numerator = np.sum((data[:len(data)-k] - mean) * (data[k:] - mean))
denominator = np.sum(np.square(data - mean))
acf_val = numerator / denominator
return acf_val
def pacf(data, k):
if k == 0:
pacf_val = 1
else:
gamma_array = np.array([acf(data, k) for k in range(1, k + 1)])
gamma_matrix = []
for i in range(k):
temp = [0] * k
temp[i:] = [acf(data, j) for j in range(k - i)] # making diagonal
gamma_matrix.append(temp)
gamma_matrix = np.array(gamma_matrix)
gamma_matrix = gamma_matrix + gamma_matrix.T - np.diag(gamma_matrix.diagonal()) # making symmetric matrix
pacf_val = np.linalg.inv(gamma_matrix).dot(gamma_array)[-1]
return pacf_val
# create a difference series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return pd.Series(diff)
# using plot_acf, plot_pacf
def draw_plot(target, data, lag):
# mean variance comparision
print("---" + target + "---")
print("mean of left group, right group: {}, {}".format(
data[:len(data) // 2].mean(), data[len(data) // 2:].mean()))
print("std of left group, right group: {}, {}\n\n".format(
data[:len(data) // 2].std(), data[len(data) // 2:].std()))
# draw original data
fig, axes = plt.subplots(2, 1, figsize=(12, 6))
plt.suptitle("Stationary " + target, fontsize=24)
axes[0].plot(data) # draw original data
sns.distplot(data, ax=axes[1]) # draw histogram to check to follow gaussian dist.
plt.show()
## ACF
print(sm.tsa.stattools.acf(data, nlags=lag, fft=False))
plot_acf(data, lags=lag, use_vlines=True)
plt.suptitle(target + " ACF", fontsize=18)
plt.xlabel("lag")
plt.show()
## PACF
print(sm.tsa.stattools.pacf(data, nlags=lag, method='ywm'))
plot_pacf(data, lags=lag, use_vlines=True)
plt.suptitle(target + " PACF", fontsize=18)
plt.xlabel("lag")
plt.show()
if __name__ == '__main__':
target = "CO2"
data = pd.read_csv("co2_time_series.csv")[target][:500]
data = difference(data)
lag = 15
acf_result = [acf(data, k) for k in range(0, lag+1)]
print(acf_result)
pacf_result = [pacf(data, k) for k in range(lag+1)]
print(pacf_result)
draw_plot(target=target, data=data, lag=lag)
관련 포스트
소스 코드

