정상성(Stationarity)
정상성(Stationarity)이란 언제 관측되는지에 관계없이 어떤 시점에 관찰하더라도 예측할 수 있는 패턴을 발견할 수 없는 것을 뜻한다.
정상성에 대한 자세한 사항은 여기를 참조하면 된다.
로그 변환(Log Transform)
비정상성 시계열을 정상성으로 변환하는 방법은 로그 변환(Log Transformation)과 차분(Differencing) 2가지가 있다.
우선 로그 변환(Log Transformation)이란 변동폭이 일정하지 않은 경우 사용할 수 있는데 일반적인 수학의 x를 log(x)로 바꾸는 변환 방식이다. 로그 변환은 원본 데이터의 왜곡을 줄이거나 제거하는데 여기서 주의할 점은 원 데이터가 로그 정규 분포를 따르거나 대략 따라줘야 한다. 그렇지 않으면 로그 변환 적용이 잘 적용되지 않는다.
이 변환 방식은 레벨-레벨(level-level), 레벨-로그(level-log), 로그-레벨(log-level), 로그-로그(log-log)가 있다. 레벨-레벨(level-level) 방식은 변환을 취하지 않으므로 설명을 생략한다. 여기서 자연로그는 ln으로 표시한다.
해당 설명은 아래 식을 기준으로 전개한다.
$$ y_i = 5 + 0.3*x_i $$
레벨-로그(level-log) 방식은 독립변수인 x에만 로그를 취하는게 가능할 때 적용할 수 있다.
$$ Y_2-Y_1 = (5+0.03ln(x_2))-(5+0.03ln(x_1)) $$
$$ Y_2-Y_1 = 0.03(ln(x_2)-ln(x_1)) $$
$$ Y_2-Y_1 = 0.03(ln(x_2/x_1)) $$
독립변수 값의 고정된 백분율 변화에 대해 종속변수가 0.03 * x 백분율 변화의 자연로그만큼 변경된다고 가정할 수 있다. 예를 들어 x가 10 % 증가하면 Y는 0.3 % 증가한다(0.03 * ln (1.1) = 0.003). x가 50 % 증가하면 Y는 1.2 % 증가한다(0.03 * ln (1.5) = 0.012). x의 백분율 변경이 고정되어 있으면 Y도 고정된 백분율로 변경된다.
로그-레벨(log-level) 방식은 종속변수에만 로그를 취할 수 있는 경우에 적용하는데, 우선 e를 밑으로 하는 독립 변수의 계수를 지수화한다.
$$ ln(Y_2)-ln(Y_1) = (5+0.03x_2)-(5+0.03x_1) $$
$$ ln(Y_2)-ln(Y_1) = 0.03(x_2-x_1) $$
$$ Y_2/Y_1 = e^{0.03(x_2-x_1)} $$
$$ Y_2/Y_1 = 1.03^{(x_2-x_1)} $$
독립변수가 1 증가할 때마다 종속 변수가 3 % (1.03¹ = 1.03) 증가한다는 결론을 내릴 수 있다. 여기서 중요한 것은 이 증가가 고정된 값이어야 한다는 것이다. x를 10 단위 늘리면 Y의 변화는 34%가 된다(1.03¹⁰ = 1.34).
로그-로그(log-log) 방식은 독립변수, 종속변수 모두 로그 변환을 취한다. 방정식의 좌변에서 로그를 제거하고 e를 밑으로하는 우변을 지수화한다.
독립변수에서 변경된 고정 백분율에 대해 종속변수가 x 백분율 변경으로 0.03의 거듭 제곱으로 변경됨을 알려준다 . x가 10 % 변하면 y는 0.3 % 변한다(1.1⁰⁰³ = 1.003). x가 20 % 변경되면 y는 0.5 % 변경된다(1.2⁰⁰³ = 1.005).
$$ ln(Y_2)-ln(Y_1) = (5+0.03ln(x_2))-(5+0.03ln(x_1)) $$
$$ ln(Y_2)-ln(Y_1) = 0.03(ln(x_2/x_1)) $$
$$ Y_2/Y_1 = e^{0.03ln(x_2/x_1)} $$
$$ Y_2/Y_1 = e^{ln(x_2/x_1)^{0.03}} $$
$$ Y_2/Y_1 = (x_2/x_1)^{0.03} $$
아래는 python으로 로그 변환을 수행한 결과이다. 로그 변환 시 변동폭이 일정해진다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("co2_data.csv")["2111PT0001"]
y = np.log(df)
plt.plot(df, label="Original")
plt.plot(y, label="log")
plt.suptitle("Log Transform", size=24)
plt.legend()
plt.show()
차분(Differencing)
차분(Differencing)이란 임의의 두 점에서 함수 값들의 차이를 의미한다. 차분을 수행하면 평균이 균일한 시계열로 변환된다. 만약 1차 차분을 진행하였을 때 정상성을 띄는 데이터로 변환하지 못했다면 차분을 2차, 3차 반복해서 수행하면 된다. 보통 1차에서 끝난다.
$$ 1차 차분: y\prime_t = y_t - y_{t-1} $$ $$ 2차 차분: y\prime\prime _t = y\prime_t - y\prime_{t-1} $$ $$ = (y_t - y_{t-1}) - (y_{t-1} - y_{t-2}) $$ $$ = y_t - 2y_{t-1} + y_{t-2} $$
하지만 데이터가 계절성을 띄는 경우엔 계절 차분(Seasonal Differencing)을 먼저 수행해주는 것이 좋다. 계절성 차분이란 관측치와 같은 계절의 이전 관측값과의 차이를 의미한다.
$$ 계절 차분: y\prime_t = y_t - y_{t-m} $$
만약 월별 계절성이 관측된다면 \(m=12\)가 될 것이고, 분기별 계절성이 나타난다면 \(m=4\)가 될 것이다.
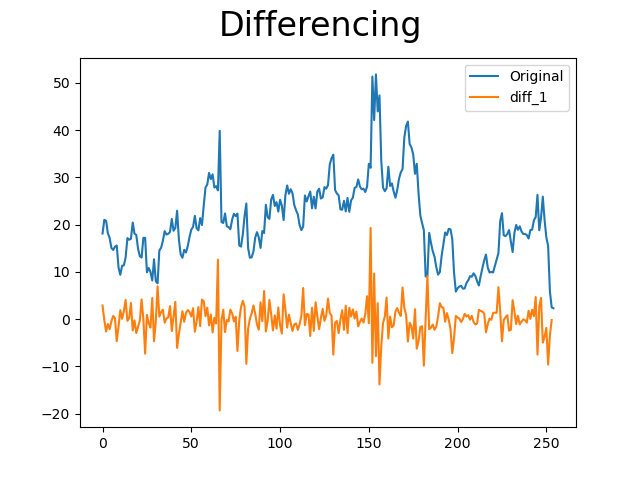
아래는 python으로 차분을 수행한 결과이다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("co2_data.csv")["2111PT0001"]
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return np.array(diff)
diff_1 = difference(df)
plt.plot(df, label="Original")
plt.plot(diff_1, label="diff_1")
plt.suptitle("Differencing", size=24)
plt.legend()
plt.show()
관련 포스트
2021.12.03 - [Data Science/Statistics] - [Python] 정상성(Stationarity)과 비정상성(Non-Stationary)
참고 자료
https://otexts.com/fppkr/stationarity.html
소스 코드

