시계열 데이터(Time Series Data)
정상성과 비정상성에 대한 구별에 앞서 시계열 데이터의 특징에 대해 간략하게 알고 넘어가는 것이 좋다. 시계열 데이터에 대한 대표적인 특징은 아래와 같다.
- Trend(추세성)
- Seasonality(계절성)
- Aberration(이변성)
- Volatility(변동성)
- Non-linearity(비선형성)
시계열 데이터는 크게 정상성 데이터와 비정상성 데이터로 나눌 수 있다.
정상성(Stationarity)
정상성(Stationarity)이란 사전적 정의로는 일정하여 늘 한결같은 성질을 의미한다. 시계열 데이터를 다룰 때 정상성 데이터는 해당 데이터가 관측된 시간과 무관한 데이터를 뜻한다. 직관적으로 보자면 데이터의 분포에서 평균과 분산이 일정하면 정상성이라고 볼 수 있다.
예를 들어 백색 잡음(White Noise) 시계열은 정상성을 나타내는 대표적인 시계열 데이터이다. 이 잡음은 모든 형태의 전자 장비와 매체에서 나타나며, 모든 범위의 주파수에 대해 균일한 전력 스펙트럼을 가지고 있다. 또한 패턴이 무작위이기 때문에 랜덤 노이즈라고도 불린다. 따라서 백색 잡음은 어느 시점에서 관찰하더라도 똑같이 관측될 수 있다.
또한 Strongly Stationary(강정상)과 Weakly Stationary(약정상)으로 나눌 수 있는데 통계적 특성이 일정한 정도에 따라 나뉘게 된다. 통상적으로 약정상 시계열도 정상성을 띄고 있다고 표현한다.
주요한 정상성의 만족 조건은 아래와 같다.
- 평균이 일정
- 분산이 시점에 의존하지 않음
- 공분산은 시차에만 의존하고, 시점 자체에 의존하지는 않음
사실 데이터만 보고 모든 경우에 정확하게 판단하는 것은 쉽지 않다. 따라서 ACF, PACF 등의 분석 방법을 통해 판별하는 것이 더 신뢰성 있는 방법이 될 수 있다.
비정상성(Non-stationary)
반면, 비정상성(Non-Stationary) 데이터는 추세(Trend)나 계절성(Seasonality)이 내포되어 있는 시계열 데이터이다. 추세와 계절성은 서로 다른 시점에 시계열의 값에 영향을 줄 수 있기 때문이다. 예를 들어 겨울에 난방비가 증가한다거나, 여름에 아이스크림 판매량이 오르는 등의 경우가 이에 해당한다.
다른 예시로는 확률 보행(random walk)이 있다. 확률 보행은 임의의 방향으로 향하는 연속적인 걸음을 나타낸다는 의미로 예측 불가능한 변동이 발생하는 것을 뜻한다. 시간과 관계없어 보여 이는 정상성 데이터로 생각할 수도 있다. 하지만 정상성 데이터가 되기 위해선 기댓값과 분산이 시간과 무관한 상수이고, 공분산은 시점(\( t \))이 아닌 시차에 관한 함수여야 한다. 확률 보행에서는 위로 올라갈 확률이나 아래로 내려갈 확률이 같기 때문에 미래 이동을 예측할 수 없으므로 예측값은 마지막 예측값과 같다고 가정하고 계산해 보면 분산이 시점(\( t \))에 의존하므로 비정상 시계열인 것을 확인할 수 있다.
$$ y_t = y_{t-1} + \epsilon_t, \epsilon_t iid(0,\sigma^2) $$
일반적으로 우리가 자주 접하게 되는 데이터는 비정상성 데이터일 가능성이 높다.
아래는 비정상성 데이터의 만족 조건이다.
- 시간에 따라 시계열의 평균 수준이 다름
- 시간에 따라 시계열의 추세를 가짐
- 시간에 따라 시계열의 계절성을 보임
- 시간에 따라 시계열의 분산이 증가하거나 감소
하지만 이런 주기성 행동을 가지고 있다고 무조건 비정상성 데이터라고 할 수는 없다. 주기성을 가지고 있지만 추세나 계절성이 없는 시계열은 정상성을 나타내는 시계열이라 볼 수 있다. 주기가 고정된 길이를 갖고 있지 않기 때문에(무한대), 미래 시계열을 관측하기 전에는 주기의 고점이나 저점이 어디일지 확실하게 알 수 없기 때문이다. 예를 들어 현재 0~5000까지의 y축 범위를 보이는 데이터가 있다고 가정한다. 이후에는 y값이 10억쯤 되는 곳에 점이 찍히게 된다면 지금의 0~5000까지의 범위는 미미한 영향으로 보일 수 있다는 것이다.
정리해보자면 정상성을 나타내는 시계열은 시간의 흐름에 따라 평균이나 분산 등의 통계적 특성이 변하지 않고, 일정한 추세가 없으며 설령 주기적인 패턴이 존재할지라도 그래프는 시계열이 일정한 분산을 갖고 대략적으로 평탄하게 표현될 것이다.
반면 비정상성 시계열의 경우 분석 시 예측 범위가 무한대이고 Variance, Autocorrelation 등 다양한 파라미터를 고려해야 한다. 따라서 정상성 변환 과정을 비정상성 데이터도 정상성으로 변환하여 분석을 진행하게 되면 예측 범위가 무한대에서 일정 범위로 줄어들어 예측 성능이 개선된다. 또한 고려할 파라미터의 수가 감소하여 단순한 알고리즘으로 예측할 수 있고, 이로 인해 over fitting도 방지할 수 있다.
변환 방법에는 평균의 정상화를 위한 차분이 있고, 분산의 안정화를 위한 자연로그 변환, 제곱/제곱근 변환 등이 있다.
대표적인 정상성 데이터인 화이트 노이즈의 패턴을 python을 이용해 구현해 보았다.
from random import gauss
from random import seed
from pandas import Series
import matplotlib.pyplot as plt
# seed random number
generator = seed(1)
# create white noise series
series = [gauss(0.0, 1.0) for i in range(1000)]
series = Series(series)
print(series.describe())
series.plot()
plt.show()
# count 1000.000000
# mean -0.013222
# std 1.003685
# min -2.961214
# 25% -0.684192
# 50% -0.010934
# 75% 0.703915
# max 2.737260
# dtype: float64
아래는 대표적인 비정상성 시계열인 확률 보행(Random Walk)을 시각화한 것이다.
import numpy as np
import matplotlib.pyplot as plt
probability = [0.5, 0.5] # [up, down]
# starting point
start = 0
rand_walks = [start]
# creating the random points
rand_point = np.random.random(300)
down_probability = rand_point < probability[0]
up_probability = rand_point >= probability[1]
# random walk process
# z(t) = z(t-1) + a(t), where a(t) is white noise
for down, up in zip(down_probability, up_probability):
rand_walks.append(rand_walks[-1] - down + up)
plt.plot(rand_walks)
plt.show()
마지막으로 비정상성 데이터로 볼 수 있는 시간별 이산화탄소 수치의 변화량이다. 재실자의 수에 따라 이산화 탄소 수치는 크게 영향을 받는다. 따라서 출퇴근 시간, 주말, 공휴일 등의 요인에 의해 계절성과 추세 등이 생긴다.
import pandas as pd
df = pd.read_csv("co2_data.csv")["co2"]
plt.plot(df)
plt.show()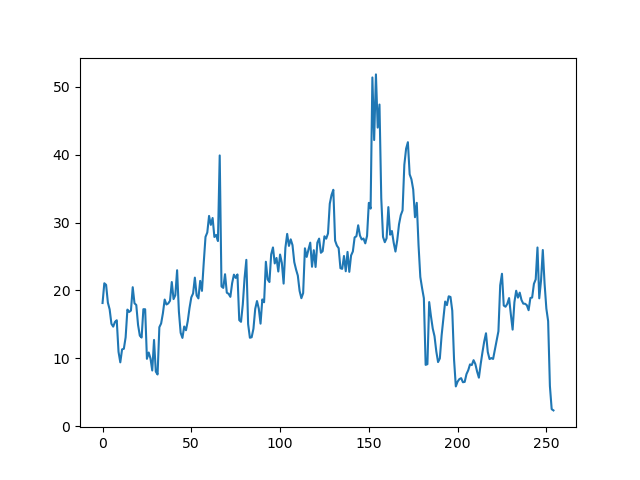
관련 포스트
참고 자료
https://otexts.com/fppkr/stationarity.html
https://datalabbit.tistory.com/111
소스 코드

