이제까지 정상성에 대한 판단 방식과 비정상성 데이터를 정상성 데이터로 바꾸는 방법들에 대해 포스팅했다. 기초적인 내용들이지만 이를 토대로 정상성 데이터를 이용한 시계열 데이터(Time Series) 예측(Forecasting)을 수행할 수 있다.
한번 더 시계열의 특성을 짚고 넘어가자면,
$$ 시계열 데이터 = 규칙적인 패턴+불규칙적인 패턴 $$
으로 볼 수 있다. 이중 규칙적인 패턴은 이전 결과 사이 발생하는 자기상관성과(Autocorrelativeness)과 이후 결과에 편향성을 초래하는 이동평균(Moving Average) 현상으로 구분할 수 있다. 반대로 불규칙적인 패턴은 white noise라 칭하고 평균이 0이며 일정한 분산을 지닌 정규분포에서 추출된 임의의 수치로 정의하고 있는데, 이런 정규분포 가정은 모델 해석을 비교적 쉽게 하도록 해주기 때문에 많은 통계 및 수치분석에서 이용되고 있다. 여기서 많이 알려진 모델들이 바로 AR모델, MA모델, ARMA모델, ARIMA 모델이다.
AR(Autoregressive)
AR(Autoregressive) 모델은 자기회귀(Autoregressive) 모델로 자기상관성을 시계열 모델로 구성한 것이다. 예측하고 싶은 특정 변수의 과거 자신의 데이터와 선형 결합을 통해 특정 시점 이후 미래값을 예측하는 모델이다. 이름 그대로 이전 자신의 데이터가 이후 자신의 미래 관측값에 영향을 끼친다는 것을 기반으로 나온 모델이다. AR(1)에 적용하기 위해선 \( -1< \phi_1 <1 \)조건이 필요하다.
AR(p)의 수식은 아래와 같다.
$$ y_t = c+\phi_1y_{t-1}+\phi_2y_{t-2}+\phi_3y_{t-3}+...+\phi_py_{t-p}+\epsilon_t $$
\( y_t \)는 \( t \)시점의 관측값, \( c \)는 상수, \( \phi \)는 가중치, \( \epsilon_t \)는 오차항을 의미한다. 오차항은 평균이 0이고 분산이 1인 정규분포에서 도출된 Random한 값이다. 아래는 AR(1) 모델이다.
$$ X(t) = c+a*X(t-1)+u*e(t) $$
수식을 보면 자기 자신을 종속변수(dependent variable)로 두고 이전의 시계열(Lag)을 독립변수(independent variable)로 가지고 식을 전개한다는 것을 알 수 있다.
MA(Moving Average)
MA(Moving Average) 모델은 예측 오차를 이용해 미래를 예측하는 모델이다. MA(q)의 수식은 아래와 같다.
$$ y_t = c+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\theta_3\epsilon_{t-3}+...+\theta_q\epsilon_{t-q}+\epsilon_t $$
여기서 \( \epsilon \)은 오차 또는 충격(shock)를 의미하며 예측이 힘든 변수로 가정한다. 아래는 MA(1) 모델이다
$$ X(t) = c+a*\epsilon_(t-1)+u*e(t) $$
자기 자신을 종속변수(dependent variable)로 두고 white noise distribution error들로 독립변수(independent variable)를 설정하는 모델이다. MA 정의상 평균과 분산이 일정하므로 정상성을 항상 만족하게 된다. 독립 항등 분포\( \epsilon_t~N(0, \sigma^2) \)이기 때문에 아래와 같이 평균과 분산을 구할 수 있다.
1. 평균=c(상수)
$$ E(y_t) = E(c+\epsilon_t+\theta_1\epsilon_{t−1}) = c $$
2. 분산=상수
$$ Var(y_t) = Var(c+\epsilon_t+\theta_1\epsilon_{t−1}) = Var(\epsilon_t)+\theta_1^2Var(\epsilon_{t-1})=(1+\theta^2_1)\sigma^2 $$
위와 같은 이유로 AR(1) 모델에선 특정한 조건이 필요한 반면 MA 모델은 모수의 제약 없이 약정상성을 띤다.
ARMA(Autoregressive and Moving Average)
ARMA(Autoregressive and Moving Average) 모델은 AR과 MA 모델을 합친것이다. 아래는 ARMA(p, q) 모델의 수식이다. 만약 ARMA(1, 0)이라면 AR(1)과 같고, ARMA(0, 1)은 MA(1)과 같다.
$$ y_t = c+\phi_1y_{t-1}+\phi_2y_{t-2}+\phi_3y_{t-3}+...+\phi_py_{t-p}+\epsilon_t+\theta_p\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\theta_3\epsilon_{t-3}+...+\theta_q\epsilon_{t-q} $$
ARMA(1, 1) 모델은 아래와 같다.
$$ X(t)=c+{a*X(t-1)}+{b*e(t-1)}+u*e(t) $$
유명한 ARMA(2, 2) 모델은 아래와 같다.
$$ X(t) = c+{a_1*X(t-1)+a_2*X(t-2)}+{b_1*e(t-1)+b_2*e(t-2)}+u*e(t) $$
ARIMA
마지막으로 ARIMA 모델이다. ARMA 모델이 과거의 데이터들을 사용하는 거에 반해 ARIMA 모델은 과거의 데이터가 지니고 있던 추세(Momentom)까지 반영한다. 여기서 추세는 자기 자신(정상 데이터)의 추세만 반응하며 white_noise는 고려하지 않는다. Correlation(연관성) 뿐 아니라 Cointegration(공적분) 까지 고려한 모델이다. 실존재하는 시계열 데이터는 불안정(Non-stationary)한 경우가 많다. 그런데 AR(p), MA(q) 모델이나, 이 둘을 합한 ARMA(p, q)모델으로는 이러한 불안정성을 설명할 수가 없다. 따라서 모델 그 자체에 이러한 비정상성을 제거하는 과정을 포함한 것이 ARIMA 모델이다. ARIMA(p, d, q)수식은 아래와 같다. d는 차분 횟수이다. 만약 ARIMA(1, 0, 0)이라면 AR(1)과 같고, ARMA(0, 0, 1)은 MA(1)과 같다.
$$ y^{'}_t = c+\phi_1y^{'}_{t-1}+\phi_2y^{'}_{t-2}+\phi_3y^{'}_{t-3}+...+\phi_py^{'}_{t-p}+\epsilon_t+\theta_p\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\theta_3\epsilon_{t-3}+...+\theta_q\epsilon_{t-q} $$
\( y^{'} \)은 차분을 구한 시계열 데이터이다. ARIMA(1, 1, 1) 모델은 아래와 같다.
$$ X(t) = \frac{[X(t-1)+{b*X(t-1)}+{c*e(t-1)}+d+u*e(t)]}{a} $$
아래의 표는 ARIMA의 여러 경우를 정리한 표이다.

이제 python으로 구현해보자. ARIMA로 다른 모델을 모두 생성할 수 있기 때문에 이번엔 ARIMA만 이용해서 구현해보도록 한다. 한 번은 차분을 적용하지 않고, 한 번은 1차 차분을 적용해 모델을 구성해보았다. 지금은 input 데이터 개수는 120개 예측할 step은 20으로 고정하고 lag은 default로 None을 넣고 실험을 진행하였다. raw data 생성 주기는 5분이다.
upper와 lower를 산정하는 방식은 statsmodels 라이브러리 내부에 있는 방식을 가져와서 사용했다. 또한 lag을 지정하지 않고 default로 사용하게 될 때는 역시 statsmodels 라이브러리 내부에 있는 _prepare_data_corr_plot 함수를 사용하여 산출했다. 이외의 이번 포스팅의 모든 함수는 동일한 upper와 lower 산정방식과 lag 설정 방식을 사용하였다. 자세한 내용들은 라이브러리 안의 함수를 직접 찾아서 보는 것도 좋을 듯하다.
차분 테스트
1. 차분하지 않았을 때
우선 PACF를 이용해 절단점을 찾고 이를 ARIMA에 적용하였다.
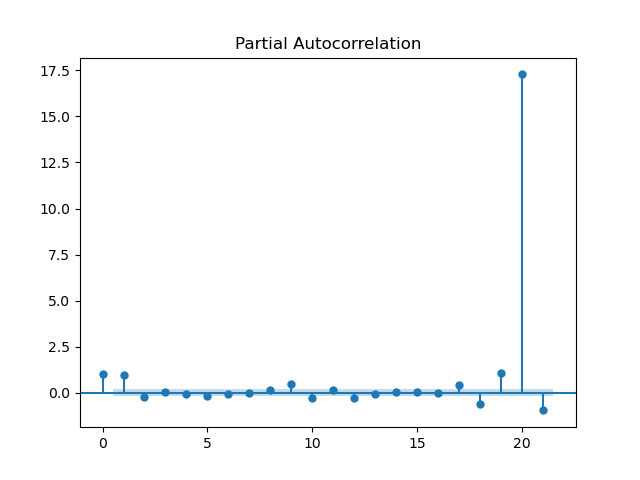
PACF는 위와 같이 나왔고 절단점은 3이라 AR(2)를 적용했다.
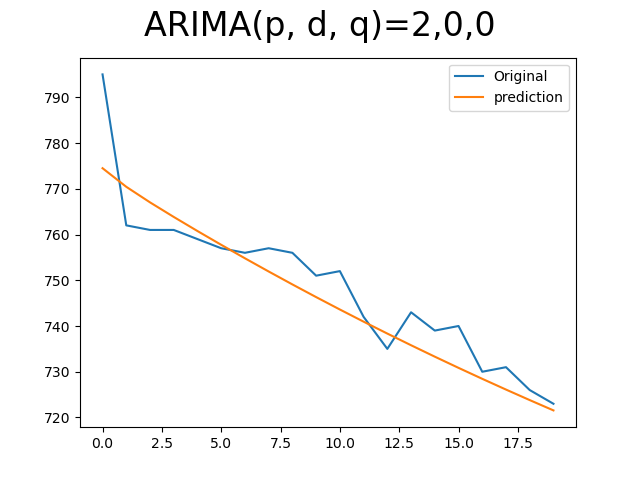
생각보다는 추세를 잘 따라갔다. 아래는 python 코드이다.
def create_AR(data, lag, future, predict_point, diff=None):
real_data = np.array(data)
if diff!=None:
data = data.diff(axis=0).dropna()
plot_pacf(data, lags=lag)
pacf, pacf_confint = sm.tsa.stattools.pacf(data, nlags=lag, alpha=0.05)
print(pacf)
plt.show()
if lag==None:
x, _, _ = _prepare_data_corr_plot(data, lag, zero=True)
else:
x = np.arange(lag + 1)
if x[0] == 0:
x = x[1:]
pacf_confint = pacf_confint[1:]
pacf = pacf[1:]
x = x.astype(float)
x[0] -= 0.5
x[-1] += 0.5
upper_limit = np.round(pacf_confint[:, 1] - pacf, 5)
lower_limit = np.round(pacf_confint[:, 0] - pacf, 5)
# set parameter
p = np.where((upper_limit>pacf)&(lower_limit<pacf))[0]
if len(p)>0:
p = p[0]
else:
p = None
if diff is not None:
d = diff
else:
d = 0
q = 0
# ARIMA prediction
if p is not None:
print()
create_ARIMA(real_data, future, p, d, q, predict_point)
이번에는 ACF를 사용하여 lag을 산출하였고 그래프는 아래와 같다.
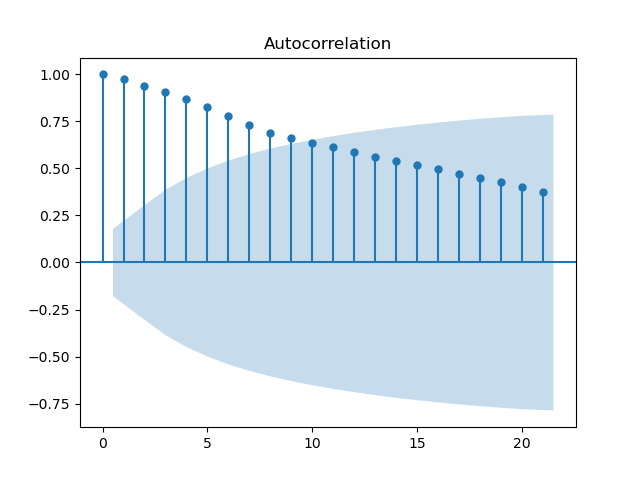
절단점이 10이라 MA(9) 모델을 산출하였다.

살짝 값의 편차가 커보이긴 하지만 어느 정도 추세는 비슷하다.
아래는 python 코드이다.
def create_MV(data, lag, future, predict_point, diff=None):
real_data = np.array(data)
if diff!=None:
data = data.diff(axis=0).dropna()
plot_acf(data, lags=lag)
acf, acf_confint = sm.tsa.stattools.acf(data, nlags=lag, alpha=0.05, fft=False)
print(acf)
plt.show()
if lag==None:
x, _, _ = _prepare_data_corr_plot(data, lag, zero=True)
else:
x = np.arange(lag + 1)
if x[0] == 0:
x = x[1:]
acf_confint = acf_confint[1:]
acf = acf[1:]
x = x.astype(float)
x[0] -= 0.5
x[-1] += 0.5
upper_limit = np.round(acf_confint[:, 1] - acf, 5)
lower_limit = np.round(acf_confint[:, 0] - acf, 5)
# set parameter
p = 0
if diff is not None:
d = diff
else:
d = 0
q = np.where((upper_limit>acf)&(lower_limit<acf))[0]
if len(q)>0:
q = q[0]
else:
q = None
# ARIMA prediction
if q is not None:
create_ARIMA(real_data, future, p, d, q, predict_point)
2. 1차 차분 적용
이번엔 1차 차분을 적용하였다. PACF를 먼저 이용해보자.
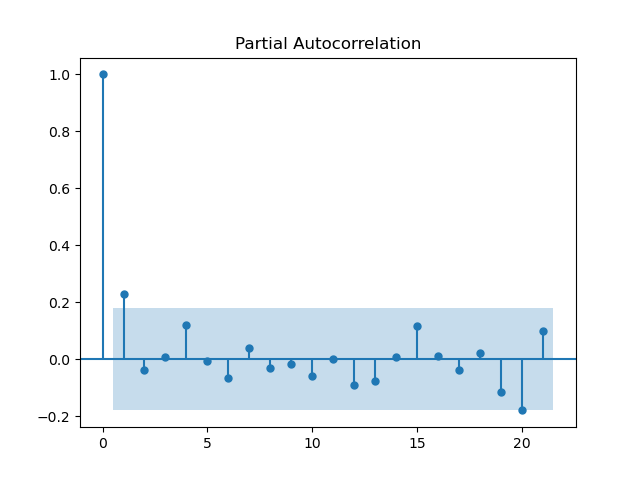
아까 차분하기 전보다 lag은 좀 줄었다. lag은 2이니 AR(1)에 넣으면 될듯하다.

1차 차분을 적용했기 때문에 d=1이다. 하지만 오히려 차분 전보다 못하다는 느낌을 받았다.
이번엔 ACF를 이용한 방식이다.

이번 역시 아까 차분하기 전보다 lag은 줄었다. lag은 이번에도 2이니 MA(1)에 넣으면 될듯하다.
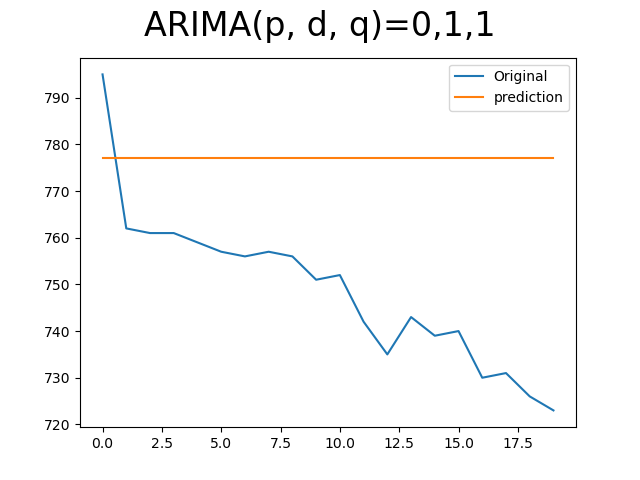
보는 것처럼 기대한 만큼의 성능은 아니다.
3. etc...
이번엔 유명한 ARMA(2, 2) 모델도 구현해 보았다.
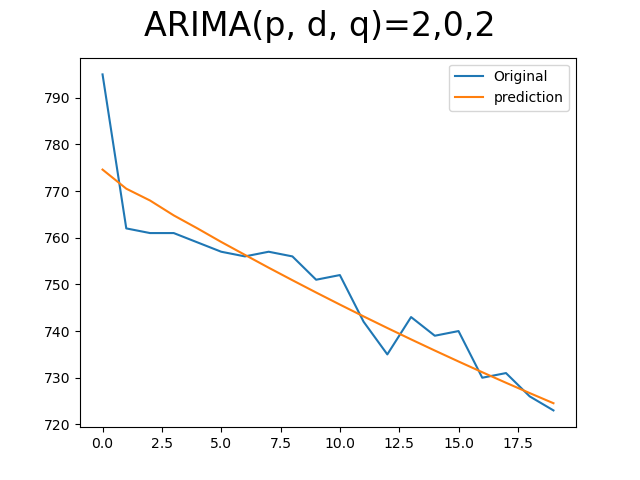
아무래도 이산화탄소 모델은 AR 모델이 더 유용하게 적용되는 듯하다.
마지막으로 그냥 마음에 드는 숫자로 넣어보았다.
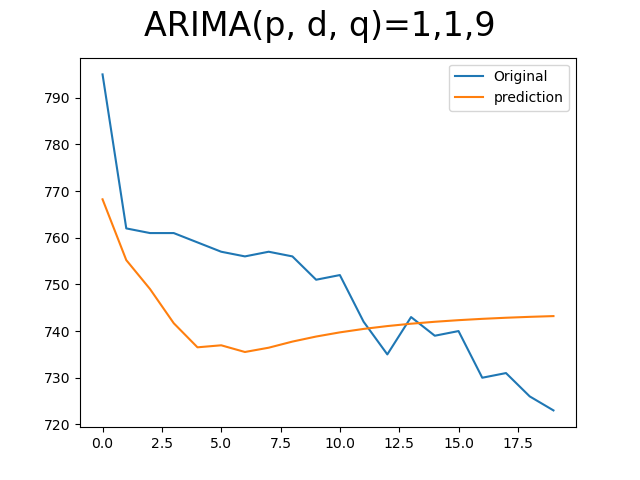
이러한 \( \hat y \)과 \( y \)값들은 MAE, RMSE 등으로 얼마나 유사한 값이 나오는지에 대한 척도를 알 수 있다.
물론 이 모델들이 잘 나오게 보이는 것처럼 보이게 하는 방법도 있다. 아래처럼 model에서 forecast가 아닌 predict 함수를 사용하면 train set과 ARIMA를 통해 나온 prediction result를 보는 방식이다. 이를 통해 나의 모델이 학습한 데이터의 추세를 어떤 식으로 따라갔는지 볼 수 있다. 하지만 원하던 결과는 미래의 값들을 예측하는 것이기에 forecast를 이용해 결과를 산출해보았다.

지금까지 만들 모델들은 예측 정확도가 지금은 그렇게 높아 보이진 않지만 더 신중하게 파라미터들을 조정하며 모델을 구상한다면 더 좋은 결과가 있을 것으로 생각된다. 또한 시계열 데이터 예측을 위해 RNN기반의 LSTM을 적용하거나 후처리 과정에서 ARIMA를 앙상블 시키는 등의 여러 고민들을 한다면 더 좋은 예측 모델을 얻을 수 있을 것으로 생각된다.
아래는 전체 python 소스 코드이다. 잘 재활용해서 유용하게 쓰이길 바란다.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf, _prepare_data_corr_plot
from statsmodels.tsa.arima.model import ARIMA
def create_AR(data, lag, future, predict_point, diff=None):
real_data = np.array(data)
if diff!=None:
data = data.diff(axis=0).dropna()
plot_pacf(data, lags=lag)
pacf, pacf_confint = sm.tsa.stattools.pacf(data, nlags=lag, alpha=0.05)
print(pacf)
plt.show()
if lag==None:
x, _, _ = _prepare_data_corr_plot(data, lag, zero=True)
else:
x = np.arange(lag + 1)
if x[0] == 0:
x = x[1:]
pacf_confint = pacf_confint[1:]
pacf = pacf[1:]
x = x.astype(float)
x[0] -= 0.5
x[-1] += 0.5
upper_limit = np.round(pacf_confint[:, 1] - pacf, 5)
lower_limit = np.round(pacf_confint[:, 0] - pacf, 5)
# set parameter
p = np.where((upper_limit>pacf)&(lower_limit<pacf))[0]
if len(p)>0:
p = p[0]
else:
p = None
if diff is not None:
d = diff
else:
d = 0
q = 0
# ARIMA prediction
if p is not None:
print()
create_ARIMA(real_data, future, p, d, q, predict_point)
def create_MV(data, lag, future, predict_point, diff=None):
real_data = np.array(data)
if diff!=None:
data = data.diff(axis=0).dropna()
plot_acf(data, lags=lag)
acf, acf_confint = sm.tsa.stattools.acf(data, nlags=lag, alpha=0.05, fft=False)
print(acf)
plt.show()
if lag==None:
x, _, _ = _prepare_data_corr_plot(data, lag, zero=True)
else:
x = np.arange(lag + 1)
if x[0] == 0:
x = x[1:]
acf_confint = acf_confint[1:]
acf = acf[1:]
x = x.astype(float)
x[0] -= 0.5
x[-1] += 0.5
upper_limit = np.round(acf_confint[:, 1] - acf, 5)
lower_limit = np.round(acf_confint[:, 0] - acf, 5)
# set parameter
p = 0
if diff is not None:
d = diff
else:
d = 0
q = np.where((upper_limit>acf)&(lower_limit<acf))[0]
if len(q)>0:
q = q[0]
else:
q = None
# ARIMA prediction
if q is not None:
create_ARIMA(real_data, future, p, d, q, predict_point)
def create_ARIMA(data, future, p, d, q, predict_point):
model = ARIMA(data, order=(p, d, q))
model_fit = model.fit()
yhat = model_fit.forecast(steps=predict_point)
# yhat = model_fit.predict(steps=predict_point)
print(model_fit.summary())
plt.plot(future, label="Original")
plt.plot(yhat, label="prediction")
plt.suptitle("ARIMA(p, d, q)="+str(p)+","+str(d)+","+str(q), size=24)
plt.legend()
plt.show()
if __name__ == '__main__':
input_point = 120
predict_point = 20
lag = None # lag default: None, or 1, 2, ...
diff = None # 차분 X: None, 1차 차분: 1, 2차 차분: 2...
df = pd.DataFrame(pd.read_csv("co2_time_series.csv")["CO2"])
data = df[:input_point]
future = np.array(df[input_point:input_point+predict_point])
create_AR(data=data, lag=lag, future=future, predict_point=predict_point, diff=diff)
create_MV(data=data, lag=lag, future=future, predict_point=predict_point, diff=diff)
관련 포스트
참고자료
https://assaeunji.github.io/statistics/2021-08-23-arima/
소스 코드

