최소 자승법(LSM or OLS)
최소 제곱법, 최소 자승법, Least Square Method(LSM), Ordinary Least Square(OLS) 모두 같은 말이다.
최소자승법(Least Square Method)은 모델의 파라미터를 구하기 위한 대표적인 방법 중 하나로서 모델과 데이터와의 잔차(residual) 제곱 합 또는 평균을 최소화하도록 파라미터를 결정하는 방법이다.
가장 간단한 관계식 \(f(x) = \beta x+\alpha\)이고, \( y_i = \alpha+\beta x_i+u_i \)가 있다고 가정한다.

위의 그래프 주어진 데이터 산포도를 그리고 임의의 회귀식(y=x, y=x+2, y=2x+1)을 그래프에 그린 것이다. 이 중 y+2를 기준으로 설명하자면 따라서 \( \alpha \)는 Y축의 절편(intercept)인 2이 되고, \(\beta\)는 직선의 기울기(tangent)인 1이 된다. 또한 \( u_i \)는 본래 오차(error-term)로 사용하지만 해당 예제에서 표본에 의해 생긴 차이이므로 잔차(residual)인 \(\epsilon_i\)라 표현할 수 있다. 또한 기울기와 절편을 선택하는 방법에 따라 방정식은 달라진다는 것을 알 수 있다.
$$ \epsilon_i = y_i-f(x_i) $$
위 모형 중 어떤 것이 가장 좋은 모델인지 생각해보자. 빨간색과 파란색이 유력해보인다. 그림만 봐서는 아직 확실한 근거가 없다. 따라서 어떤 절편과 기울기 수치가 가장 이 표본 데이터를 잘 설명하는 것인지 찾기 위하여 잔차가 가장 최소화되는 파라미터(기울기와 절편)를 찾는다. 그리고 아래 식을 최소화시키는 것이 최소자승법이다.
$$ \sum_{i=1}^{n}\epsilon_i = \sum_{i=1}^{n}(y_i-f(x_i))^2 $$
$$ \sum_{i=1}^{n}(y_i-\beta x_i-\alpha)^2 $$
$$ OLS = Min(\sum_{i=1}^{n}(y_i-\beta x_i-\alpha)^2) $$
하지만 최소자승법(Least Square Method)은 어떤 기준을 가지고 모델의 파라미터를 구하는가를 말해줄 뿐 실제로 이걸 어떻게 계산하는가는 별개의 문제이다. 실제 계산을 못한다면 활용하기 힘든 만큼 최소자승법을 어떻게 계산하느냐도 매우 중요하다. 최소자승법을 계산하는 방법은 크게 해석학적(analytic) 방법과 대수적(algebraic) 방법이 있는데 대수적 방법이 훨씬 직관적이면서도 효과적이다.
대수적(Algebraic) 방법
먼저, 대수적(Algebraic) 방법은 위의 모델 추정 문제를 행렬식 형태로 계산한다. 위에서 예로 든 직선 f(x) = ax +b 추정 문제는 결국 다음 식들을 만족하는 a, b를 찾는 것이다.
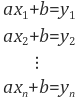
이를 행렬식으로 표현하면 다음과 같다.


이 때, A의 역행렬은 존재하지 않지만 pseudo inverse라는 걸 이용하면 X를 다음과 같이 계산할 수 있다.

해석학적 방법(Analytic)
해석학적(Analytic) 방법은 \( \sum_{i=1}^{n}(y_i-\beta x_i-\alpha)^2 \)을 각각의 모델 파라미터들로 편미분한 후에 그 결과를 0으로 놓고 연립 방정식을 푸는 것이다. \( f'(x)=0, f''(x)>0 \)을 사용한다. 우선 f'(x)=0가 만족하는지 알기 위해 \( \alpha, \beta \)를 찾아야 하고, 편미분을 통해 찾아준다.
$$ \frac{∂S}{∂\alpha} = -2\sum_{i=1}^{n}(y_i-\beta x_i-\alpha) = 0$$
$$ \frac{∂S}{∂\beta} = -2\sum_{i=1}^{n}(y_i-\beta x_i-\alpha) = 0$$
위 두 수식을 정리하면
$$ \alpha n + \beta\sum{x_i} = \sum{y_i} $$
$$ \alpha\sum{x_i}+\beta\sum{x_i^2} = \sum{x_i}{y_i} $$
이 되는데, 이 정리된 식이 정규방정식(Normal Equations)이다. 하지만 이 식은 최소 or 최대 점을 찾는 것으로 이 점이 최소가 되려면 f"(x)>0 조건도 만족해야 한다. 이를 위해 이차 편미분 행렬을 사용해야 하는데 자세한 내용은 여기를 참조바란다. 두 번째 조건을 충족하면 아래와 같이 \( \alpha, \beta \)를 구할 수 있다.
$$ \beta=\frac{\sum{(x_i-\bar{x_i})(y_i-\bar{y_i})}}{\sum(x_i-\bar{x})^2} $$
$$ \alpha=\frac{\sum{y_i}}{n}-b_1\frac{\sum{x_i}}{n}=\bar{y}-\beta\bar{x} $$
이다.
\( y=wx+b \)에서 w=\(\beta\)이고, b=\(\alpha\)일때,
$$ w=\frac{\sum{(x_i-\bar{x_i})(y_i-\bar{y_i})}}{\sum(x_i-\bar{x})^2} $$
$$ b=\bar{y}-a\bar{x} $$
이다.
실습
이제 python을 이용해 최소자승법(OLS)을 구현해보았다. 여기선 직접 구현, statsmodel, sklearn을 이용해 구현해보았다.
1. 직접 만들기

위 그래프 붉은 선에 해당하는 함수에 노이즈를 섞어 데이터를 생성하였다.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def make_data(w=0.5, b=0.8, size=50, noise=1.0):
x = np.arange(size)
y = w * x + b
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
return x, yy
def make_linear(w=0.5, b=0.8, size=50, noise=1.0):
x, yy = make_data(w=w, b=b, size=size, noise=noise)
plt.figure(figsize=(10, 7))
plt.plot(x, y, color='r')
plt.scatter(x, yy, label='data')
plt.legend(fontsize=20)
plt.title(label=f'y = {w}*x + {b}')
plt.show()
print(f'w: {w}, b: {b}')
return x, yy
# beta=w=기울기, alpha=b=절편
beta = 0.8
alpha = 2
x, y = make_linear(size=100, w=beta, b=alpha, noise=6)
# y[5]=60 # noise
# y[10]=60 # noise
x_bar = x.mean()
y_bar = y.mean()
calculated_weight = ((x - x_bar) * (y - y_bar)).sum() / ((x - x_bar)**2).sum()
print('w: {:.2f}'.format(calculated_weight))
calculated_bias = y_bar - calculated_weight*x_bar
print('b: {:.2f}'.format(calculated_bias))
# w: 0.79
# b: 2.94
직접 구현한 OLS에서 w는 0.79, b는 2.94로 y=0.79x+2.94라는 회귀 식이 도출되었다.
최소 자승법은 여러 회귀 모델에서 효율적으로 이용할 수 있지만 노이즈(noise or outlier)에 취약하다는 한계가 있다. 따라서 outlier가 존재하는 경우에는 RANSAC, LMedS, M-estimator 등과 같은 robust한 파라미터 추정 방법을 사용해야 한다.

x, y = make_linear(size=100, w=beta, b=alpha, noise=6)
y[5]=60 # noise
y[10]=60 # noise
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.show()
x_bar = x.mean()
y_bar = y.mean()
calculated_weight = ((x - x_bar) * (y - y_bar)).sum() / ((x - x_bar)**2).sum()
print('w: {:.2f}'.format(calculated_weight))
calculated_bias = y_bar - calculated_weight*x_bar
print('b: {:.2f}'.format(calculated_bias))
# w: 0.74
# b: 5.82
b(편향)이 증가한 것이 확인된다. outlier가 존재할 때 w는 0.74, b는 5.84로 y=0.74x+5.82라는 회귀 식이 도출되었다.
2. statsmodels
다음은 statsmodels.api의 OLS 함수를 사용한 결과이다.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
def make_data(w=0.5, b=0.8, size=50, noise=1.0):
x = np.arange(size)
y = w * x + b
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
return x, yy
def OLS(x, y):
df = pd.DataFrame(x, columns=["x"])
df['y'] = y
df['intercept'] = 1
model = sm.OLS(df['y'], df[['intercept', 'x']])
results = model.fit()
print(results.summary())
res = results.params['x']*x + results.params['intercept']
plt.figure(figsize=(10, 7))
plt.plot(res, color='red')
plt.scatter(x, y)
plt.suptitle("OLS")
plt.title('y = ' + str(round(results.params['x'], 3))+'*x+' + str(round(results.params['intercept'], 3)))
plt.show()
return results.params['x'], results.params['intercept']
beta = 0.8
alpha = 2
x, y = make_data(size=100, w=beta, b=alpha, noise=6)
OLS(x, y)
# w: 0.82
# b: 0.19
w는 0.82, b는 0.19로 y=0.82x+0.19라는 회귀 식이 도출되었다.
아래는 results.summary()에서 print되는 결과이다.
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.981
Model: OLS Adj. R-squared: 0.981
Method: Least Squares F-statistic: 5173.
Date: Mon, 21 Feb 2022 Prob (F-statistic): 1.28e-86
Time: 18:19:02 Log-Likelihood: -260.95
No. Observations: 100 AIC: 525.9
Df Residuals: 98 BIC: 531.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.1962 0.660 0.297 0.767 -1.113 1.505
x 0.8278 0.012 71.923 0.000 0.805 0.851
==============================================================================
Omnibus: 18.976 Durbin-Watson: 2.308
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4.864
Skew: 0.073 Prob(JB): 0.0879
Kurtosis: 1.929 Cond. No. 114.
==============================================================================
- R-squared는 결정계수, Adj. R-squared는 조정된 결정계수를 의미한다. 결정계수에 대한 추가적인 내용은 여기를 참조하면 된다.
- F-statistic는 회귀모형에 대한 (통계적) 유의미성 검증 결과이다.
- Log likelihood는 R제곱과 마찬가지로 독립변수가 많아지면 증가한다. 우도와 관련된 내용은 여기에 조금 더 자세한 설명이 있다.
- AIC, BIC는 로그 우도를 독립변수의 수로 보정한 값이고 작을수록 좋다. AIC, BIC 관련 추가적인 내용은 여기에 있다.
- coef는 각 인자에 곱해져야 할 계수이며 intercept는 1이므로 저 값을 그대로 사용하고, x의 coef는 0.8278x와 같이 회귀식에 대입하면 된다.
- P>|t|는 모집단에서 계수가 0일 때, 현재와 같은 크기의 표본에서 이러한 계수가 추정될 확률인 p값을 나타낸다.
이 확률이 매우 작다는 것은, 모집단에서 x의 계수가 정확히 0.8278은 아니더라도 현재의 표본과 비슷하게 0보다 큰 어떤 범위에 있을 가능성이 높다는 것을 의미한다. 보통 5%와 같은 유의수준을 정하여 p값이 그보다 작으면(p<0.05), 통계적으로 유의미하다고 한다. 반대로 intercept는 유의미하지 않다.
3. sklearn
이제 sklearn.linear_model의 LinearRegression 함수를 사용해 w와 b를 도출한다.

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
def make_data(w=0.5, b=0.8, size=50, noise=1.0):
x = np.arange(size)
y = w * x + b
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
return x, yy
def LR(x, y):
model = LinearRegression()
model.fit(x.reshape(-1, 1), y)
res = model.coef_[0]*x + model.intercept_
print('w: {:.2f}, b: {:.2f}'.format(model.coef_[0], model.intercept_))
plt.figure(figsize=(10, 7))
plt.plot(res, color='red')
plt.scatter(x, y)
plt.suptitle("LR")
plt.title('y = ' + str(round(model.coef_[0], 3))+'*x+' + str(round(model.intercept_, 3)))
plt.show()
return model.coef_[0], model.intercept_
beta = 0.8
alpha = 2
x, y = make_data(size=100, w=beta, b=alpha, noise=6)
LR(x, y)
# w: 0.82
# b: 0.19
w는 0.82, b는 0.19로 y=0.82x+0.19라는 회귀 식이 도출되었다.
아래는 전체 python 소스 코드이다.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
def make_data(w=0.5, b=0.8, size=50, noise=1.0):
x = np.arange(size)
y = w * x + b
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise # 노이즈 추가
return x, yy
def make_linear(w=0.5, b=0.8, size=50, noise=1.0):
x, yy = make_data(w=w, b=b, size=size, noise=noise)
plt.figure(figsize=(10, 7))
plt.plot(x, y, color='r')
plt.scatter(x, yy, label='data')
plt.legend(fontsize=20)
plt.title(label=f'y = {w}*x + {b}')
plt.show()
print(f'w: {w}, b: {b}')
return x, yy
# beta=w=기울기, alpha=b=절편
beta = 0.8
alpha = 2
x, y = make_linear(size=100, w=beta, b=alpha, noise=6)
# y[5]=60 # noise
# y[10]=60 # noise
x_bar = x.mean()
y_bar = y.mean()
calculated_weight = ((x - x_bar) * (y - y_bar)).sum() / ((x - x_bar)**2).sum()
print('w: {:.2f}'.format(calculated_weight))
calculated_bias = y_bar - calculated_weight*x_bar
print('b: {:.2f}'.format(calculated_bias))
def OLS(x, y):
df = pd.DataFrame(x, columns=["x"])
df['y'] = y
df['intercept'] = 1
model = sm.OLS(df['y'], df[['intercept', 'x']])
results = model.fit()
print(results.summary())
res = results.params['x']*x + results.params['intercept']
plt.figure(figsize=(10, 7))
plt.plot(res, color='red')
plt.scatter(x, y)
plt.suptitle("OLS")
plt.title('y = ' + str(round(results.params['x'], 3))+'*x+' + str(round(results.params['intercept'], 3)))
plt.show()
return results.params['x'], results.params['intercept']
def LR(x, y):
model = LinearRegression()
model.fit(x.reshape(-1, 1), y)
res = model.coef_[0]*x + model.intercept_
print('w: {:.2f}, b: {:.2f}'.format(model.coef_[0], model.intercept_))
plt.figure(figsize=(10, 7))
plt.plot(res, color='red')
plt.scatter(x, y)
plt.suptitle("LR")
plt.title('y = ' + str(round(model.coef_[0], 3))+'*x+' + str(round(model.intercept_, 3)))
plt.show()
return model.coef_[0], model.intercept_
x, y = make_data(size=100, w=beta, b=alpha, noise=6)
OLS(x, y)
LR(x, y)
최소 자승법은 포물선 근사, 영상의 밝기 보정, 모션 추정하기 등에도 활용할 수 있다고 한다.
참고 자료
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=dhkdwnddml&logNo=220156712894
https://darkpgmr.tistory.com/56
https://bkshin.tistory.com/entry/DATA-17-Regression
https://laoonlee.tistory.com/14
https://teddylee777.github.io/scikit-learn/linear-regression
소스 코드

