모든 데이터를 하나의 회귀식으로 설명하기는 힘들다. 또한 절대적인 회귀식을 도출하는 것도 쉽지 않다. 일반적으로 표본이란 것 자체가 대표성을 갖긴 하지만 모집단 그 자체가 될 순 없기 때문이다. 그러므로 관측값과 기댓값의 차이를 어느 정도 인정하고 진리에 가까울 것으로 추정되는 회귀식을 도출한다. 이때 차이를 의미하는 단어들이 있다.
편차(Deviation)와 표준편차(SD, Standard Deviation)
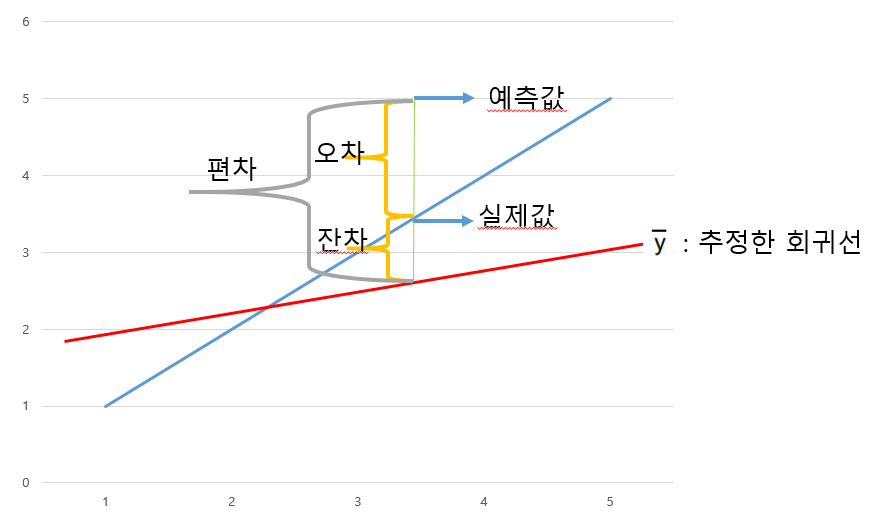
우선 편차(deviation)는 관측치가 평균으로 부터 떨어져 있는 정도, 즉 평균과 관측치와의 차이를 의미한다. 이 중 표준편차(SD, Standard Deviation)는 이러한 편차들의 평균값으로 평균으로부터 얼마나 떨어져 있는가에 대한 정보를 제공한다. 또한 표준편차를 통해 관측값들이 집합 내에서 평균과 어느 정도 떨어져 있는지 알 수 있다.
표준편차의 공식은 자료가 모집단인지 아니면 모집단을 대표하는 표본집단인지에 따라 달라진다.
예를 들어 자료가 모집단인 경우, 데이터 값의 개수 N으로 나누고,
자료가 모집단을 대표하는 표본집단이라면 표본에 있는 자료값의 개수보다 작은 n-1로 나눈다.
n-1로 나누는 자세한 이유는 간략하게 설명하자면 불편성(unbiasedness) 혹은 불편추량(unbiased estimator), 자유도(degree of freedom)때문이지만 증명을 보고싶다면 여기를 참고바란다.
$$ 모표준편차(\sigma) = \sqrt{ \frac{(x_i-μ)^2}{N}} $$
$$ 표본표준편차(s_x)=\sqrt{\frac{\sum{(x_i-\bar{x})^2}}{n-1}} $$
오차(error)
다음으로 오차(error)는 모집단(population)으로부터 추정한 회귀식으로부터 얻은 예측값과 실제 관측값의 차이이다. 즉, 오차는 추정한 회귀식과 모집단에서의 관측값의 차이 뜻한다. 표준오차(Standard Error)는 표본추출의 과정에서 발생하는 오차와 연관된 것으로 추정량의 정도를 나타내는데, 표본이 모집단으로부터 얼마나 떨어져 있는지를 나타내는 것이다.
$$ 표준오차(SE)=\frac{\sigma}{\sqrt{n}} $$
$$ 오차율=\frac{|이론값-측정값| * 100}{이론값} $$
잔차(residual)
반면 잔차(residual)는 표본집단(sample)에서 회귀식을 얻었을 때, 그 회귀식을 통해 얻은 예측값과 실제 관측값의 차이를 의미한다. 일반적으로 표본집단에서 회귀식을 얻기 때문에, 잔차를 이용해 회귀식의 최적 파라미터 값을 추정한다. 즉, 잔차들의 제곱들을 더한 것(잔차 제곱합)을 최소로 만들어주는 파라미터를 찾는 것이 최소 제곱 법(least squares method) 또는 최소자승법이다.
오차와 잔차가 같은 말처럼 보이기도 한다. 실제로 많은 사람들이 오차와 잔차를 구분없이 혼동해서 사용한다.
사실상 우리는 대부분 표본집단에서 회귀식을 얻기 때문에, 잔차를 이용하여 회귀식의 최적의 파라미터 값들을 추정한다.
참고 자료
https://ysyblog.tistory.com/160

