회귀 분석을 수행하며 자주 보이는 r2 score와 관련된 지표인 SST, SSE, SSR이 가지는 의미에 대해 살펴본다.
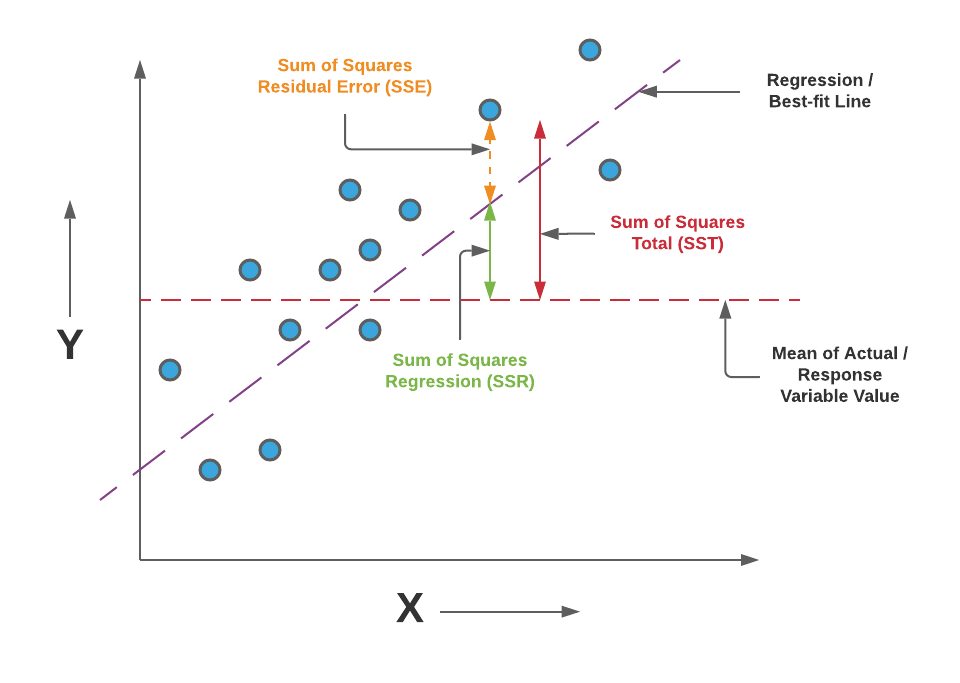
SST는 총 제곱합, SSR은 회귀식 추정 값과 관측값의 평균 간 차이인 회귀 제곱합을 나타낸다. SSE는 잔차 제곱합이다. 경우에 따라 SSE와 SSR을 바꿔 표기하는 경우도 있는데 이때 식을 잘 봐야 한다. 수식에 사용되는 값은 아래와 같다.
- \( {y}_i \): 관측값
- \( \overline{y} \): 관측값의 평균
- \( \hat{y_i}\): 예측값
SST(Total Sum of Squares)
우선 SST(Total Sum of Squares)는 관측값에서 관측값의 평균(혹은 추정치의 평균)을 뺀 결과의 총합인 총 제곱합이다. 이는 전체(Total)에 대한 변동성을 나타낸다. 그리고 SST는 SSR과 SSE의 합이다.
SST 수식은 아래와 같다.
$$ SST = SSR+SSE $$
$$ SST\ = \ \sum _{i=1}^n{\left({y}_i-\overline {y}\right)}^2 $$
SSR(Sum of Squares due to Regression)
- 회귀 제곱합
- SSR(Sum of Squares due to Regression)
- ESS(Explained Sum of Squares)
이는 회귀식으로 부터 나온 예측값에서 관측값(y)의 평균(혹은 추정치의 평균)을 뺀 결과의 총합이며 분석을 통해 설명 가능한 수치이다. 그러므로 직선(Regression)에 대한 변동성을 나타낼 수 있다. SSR 수식은 아래와 같다.
$$ SSR\ =\ \sum _{i=1}^n{\left(\hat{{y}_i}-\overline {y}\right)}^2 $$
SSE(Sum of Squares Residual of Error)
- 잔차 제곱합
- SSE(Sum of Squares Residual of Error)
- SSR(Sum of Squared Residual)
- RSS(Residual sum of squares)
이는 실제 관측값(y)과 예측값 사이의 차인 잔차(Residual)의 총합을 뜻한다. 예측값과 실제 관측값의 차이가 있을 수 있으며 이는 회귀식으로는 설명할 수 없는 설명 불가능한 수치이다. SSE값은 오차(Error)에 대한 변동성을 나타내는데, 이 값이 작을수록 좋은 모델이라 볼 수 있다. 자주 사용되는 MSE(Mean Squared Error)는 SSE를 표준화한 개념이다. SSE 수식은 아래와 같다.
$$ SSE\ =\ \sum _{i=1}^n{\left({y}_i-\hat{{y}_i}\right)}^2 $$
위의 수식에 따라 결국 SST=SSR+SSE이며, SSR과 SSE는 반비례 관계라는 것을 알 수 있다.
추가적으로 총 변동 중 설명 가능한 변동의 비율을 뜻하는 결정계수(\( R^2 \))는 아래와 같은 식이 성립한다.
$$ R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST} $$
이름을 저렇게들 붙인 이유는 알겠지만 상당히 헷갈린다. 첫 댓글을 보고 수식과 약어의 명칭이 반대로 된 것을 보고 다시 바로잡았다.
위 약어가 설명 가능 수치일 때 R을 Regression, E를 Explained로 생각하고, 설명 불가능 수치일 때는 R을 Residual, E를 Error로 생각하면 좀 더 쉽게 구분할 수 있다. 그래도 수식을 보고 판단하는 습관을 기르는 것이 좋다.
관련 포스트
참고 자료
https://sosoeasy.tistory.com/371
https://m.blog.naver.com/tlrror9496/222055889079

