반응형
주요 개념
- 이상치(Outlier)
- IQR(Interquartile Range)
이상치(Outlier)는 현재 가지고 있는 데이터 표본에 일관성 또는 연관성이 떨어지는 부분이다. 데이터 수집 장치 또는 수신부의 이상으로 인해 노이즈가 섞이는 경우 등 이런 이상치가 포함될 수 있다. 따라서 데이터를 정제하는 과정 중 이상치 제거는 필수적인 부분이다. EDA 과정 중 1차적으로 결측치와 이상치 등을 판단해 필터링을 수행해야 하는데, 이때 IQR(Interquartile Range)을 통해 이상치에 대한 판단을 할 수 있다. IQR은 분위(Quantile)라는 개념에 기초한다.
전체 데이터들을 오름차순으로 정렬하고, 정확히 4등분(25%, 50%, 75%, 100%)으로 나누는데 이 때 Q3(75%) - Q1(25%)를 한 값을 IQR(Interquartile Range)이라고 한다.
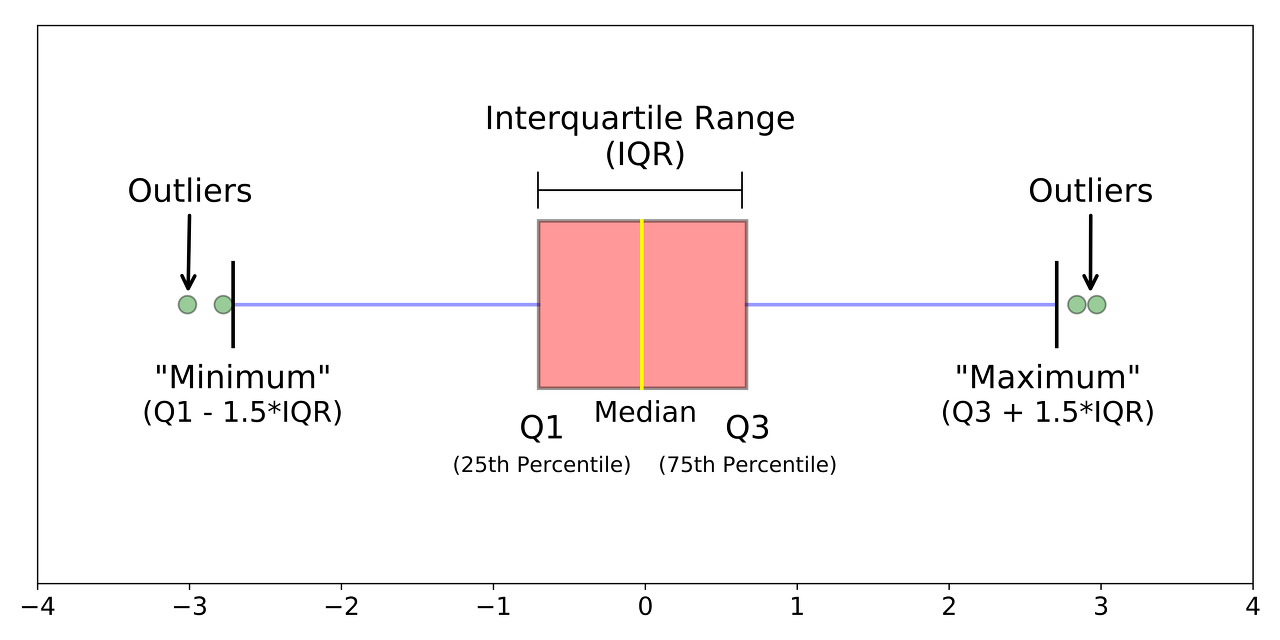
Python에서 IQR은 직접 구현하거나 pandas 라이브러리의 Dataframe에서 describe 또는 quantile 함수를 이용해 구할 수 있다. 차분을 수행하기 전과 차분을 수행한 후 IQR 제거를 수행해보았다.
import numpy as np
import pandas as pd
DATASET_PATH = 'data/0326_0927/co2_time_series.csv'
## load data
target = 'CO2'
df = pd.read_csv(DATASET_PATH, parse_dates=['Date'], index_col='Date')
def outlier_iqr(data):
q25, q75 = np.quantile(data, 0.25), np.quantile(data, 0.75)
iqr = q75 - q25
cut_off = iqr * 1.5
lower, upper = q25 - cut_off, q75 + cut_off
print('IQR은', iqr, '이다.')
print('lower bound 값은', lower, '이다.')
print('upper bound 값은', upper, '이다.')
# 1사 분위와 4사 분위에 속해있는 데이터 각각 저장하기
data1 = data[data > upper]
data2 = data[data < lower]
# 이상치 총 개수 구하기
print('총 이상치 개수는', data1.shape[0] + data2.shape[0], '이다.\n')
return lower, upper
outlier_iqr(df[target])
## quantile 이용
Q1_quantile = df[target].quantile(.25)
Q2_quantile = df[target].quantile(.50)
Q3_quantile = df[target].quantile(.75)
## describe 이용
des = df[target].describe()
Q1_describe = des["25%"]
Q2_describe = des["50%"]
Q3_describe = des["75%"]
# create a differenced series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return np.array(diff)
data = difference(df[target])
outlier_iqr(data)
# original
# IQR은 219.0 이다.
# lower bound 값은 66.5 이다.
# upper bound 값은 942.5 이다.
# 총 이상치 개수는 1662 이다.
# 차분
# IQR은 9.0 이다.
# lower bound 값은 -18.5 이다.
# upper bound 값은 17.5 이다.
# 총 이상치 개수는 6458 이다.
참고 자료
소스 코드
반응형

