주요 개념
- 귀무가설
- 대립가설
- ANOVA(Analysis Of Variance, 분산 분석)
ANOVA(Analysis Of Variance, 분산 분석)은 독립 변수가 하나이고 측정 집단이 3개 이상인 다수 집단의 평균(또는 산술 평균)에서 분산 값을 비교하는 데 사용되는 통계 공식이다.

- A 그림: ANOVA 분석 결과, 그룹 사이의 차이가 없음
- B 그림: ANOVA 분석 결과, 그룹 사이의 유의한 차이가 존재
예를 들어, 과학자들은 다양한 당뇨병 약물의 효과를 연구할 목적으로 약물 유형과 그에 따른 혈당 수치 사이의 관계를 설정하고 실험하여 조사했다 가정한다. 이때 표본 집단은 사람들의 집합이다. 샘플 모집단을 여러 그룹으로 나누고 각 그룹은 시험 기간 동안 특정 의약품을 투여받는다. 시험 기간이 끝나면 각 대상자의 혈당 수치를 측정한다. 그런 다음 각 그룹에 대해 평균 혈당 수치를 계산한다. ANOVA는 이러한 그룹 평균을 비교하여 통계적으로 다른지 또는 유사한 지 알 수 있다.
ANOVA의 결과는 'F 통계량'이다. 이 비율은 그룹 내 분산과 그룹 간 분산 간의 차이를 보여주며, 최종적으로 귀무 가설이 기각 또는 채택된다는 결론을 내릴 수 있다. 그룹 간에 유의한 차이가 있는 경우 귀무 가설은 기각되며 F 비율이 더 커진다. 여기서 귀무가설(H0)은 그룹 또는 평균 간에 차이가 없는 경우이고, 대립 가설(H1)은 그룹과 평균 사이에 차이가 있다는 가설이 있는 경우이다. ANOVA 검정의 결과에 따라 귀무가설이 채택 또는 기각된다.
ANOVA의 유형은 아래와 같다.
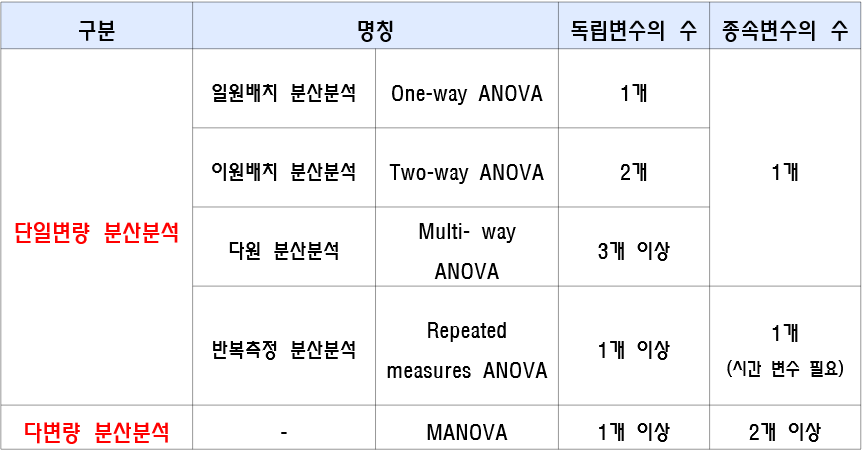
각 유형별 간단한 예시는 아래와 같다.
일원(배치) 분산분석(One-way ANOVA)
- 예) 축구 선수 A/B/C 간 훈련 시간에 따른 패스 성공률 비교(독립 변인: 훈련 시간, 종속 변인: 패스 성공률)
이원(배치) 분산분석(Two-way ANOVA)
- 예) 축구 선수 A/B/C 간 훈련 시간과 IQ에 따른 성적 비교(독립 변인: 훈련 시간/IQ, 종속 변인: 패스 성공률)
다변량 분산분석(multiple analysis of variance, MANOVA)
- 예) 축구 선수 A/B/C 간 훈련 시간에 따른 체중과 패스 성공률 비교 (독립 변인: 훈련 시간, 종속 변인: 체중/패스 성공률)
ANOVA는 평균값의 차이가 통계적으로 유의한지 확인할 수 있다. 또한 독립 변수가 종속 변수에 영향을 미치는지를 간접적으로 나타낼 수 있다. 예를 들어, 위의 혈당 수준 실험에서는 ANOVA가 그룹 평균이 통계적으로 유의하지 않고 그룹 평균 간의 차이가 샘플링 오류 때문이라는 것을 발견했다고 가정한다. 이를 통해 약물의 유형(독립 변수)이 혈당 수치(종속 변수)에 영향을 미치는 중요한 요소가 아니라는 것을 추론할 수 있다.
하지만 ANOVA는 최소 두 그룹의 평균간에 유의한 차이가 있는지 여부만 알 수 있고 어떤 쌍에서 평균이 다른지는 설명할 수 없다. 세분화된 데이터에 대한 요구 사항이 있는 경우 추가 후속 통계 프로세스를 배포하면 평균값이 다른 그룹을 찾는 데 유용하다. 그러므로 ANOVA는 다른 통계 방법과 함께 사용된다.
ANOVA는 또한 평균만 비교하기 때문에 데이터 세트가 균일하게 분포되어 있고 표준 편차가 그룹 간에 동일하거나 유사하다 가정한다. 데이터가 정규 곡선 형태로 분포되어 있지 않고 특이치가 있는 경우 ANOVA는 데이터를 해석하는 데 적합한 프로세스가 아니다. 따라서 표준 편차에 큰 차이가 있으면 검정의 결론이 정확하지 않을 수 있다.
그럼에도 ANOVA를 통해 머신 러닝의 가장 큰 과제 중 하나는 모델을 학습시 가장 적합한 기능을 선택할 수 있다. 또한 모델의 복잡성을 줄이기 위해 입력 변수의 수를 최소화하기 위해 사용될 수 있고, 독립 변수가 목표 변수에 영향을 미치는지 확인하는 데 도움이 된다.
예를 들어 스팸메일을 감지하거나 세 가지 다른 비료 제품을 사용한 두 가지 다른 밀 품종의 수확량 비교분석, 특정 제품의 판매에 대한 다양한 소셜 미디어 광고의 효과 비교, 다양한 유형의 차량에서 다양한 윤활유의 효과 비교 등에 사용될 수 있다.
아래는 일원 분산 분석을 수행한 python 소스 코드이다. a ,b c는 각각 시험 점수라 가정한다.
a = [66, 74, 82, 75, 73, 97, 87, 78]
b = [72, 51, 59, 62, 74, 64, 78, 63]
c = [61, 60, 57, 60, 81, 55, 70, 71]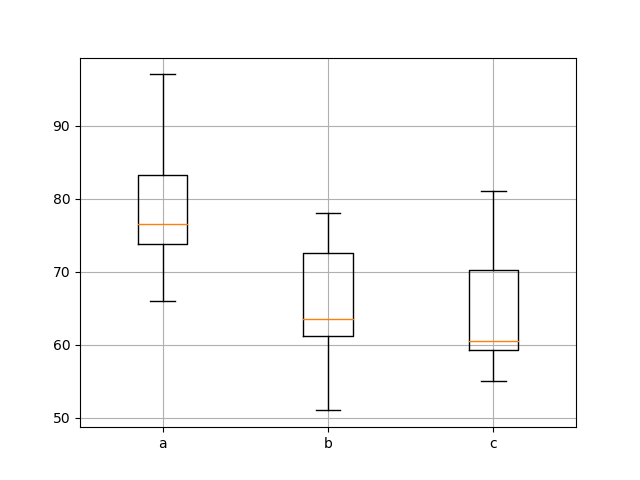
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
a = [66, 74, 82, 75, 73, 97, 87, 78]
b = [72, 51, 59, 62, 74, 64, 78, 63]
c = [61, 60, 57, 60, 81, 55, 70, 71]
print("a 평균 : ", np.mean(a))
print("b 평균 : ", np.mean(b))
print("c 평균 : ", np.mean(c))
plot_data = [a, b, c]
plt.boxplot(plot_data)
plt.xticks([1, 2, 3],['a', 'b', 'c'])
plt.grid(True)
plt.show()
F_statistic, pVal = stats.f_oneway(a, b, c)
print('F={0:.1f}, p-value={1:.3f}'.format(F_statistic, pVal))
# a 평균 : 79.0
# b 평균 : 65.375
# c 평균 : 64.375
# F=6.5, p-value=0.006
관련 포스트
참고 자료
https://bioinformaticsandme.tistory.com/198
https://www.tibco.com/ko/reference-center/what-is-analysis-of-variance-anova
https://kwon-coach.tistory.com/76
https://heannim-world.tistory.com/61
사후 검정 관련 포스팅
https://m.blog.naver.com/statsol/221472155248
소스코드

