가설검정
가설검정이란 귀무가설과 대립가설을 세워 이 둘 중 어느 것이 참인 것인지 밝혀내는 검정방식이다.
일반적으로 귀무가설(H0)은 처음부터 버릴 것이라 생각하고 설정하는 가설이다. 반대로 대립가설(H1)은 귀무가설이 기각되었을 때 자동으로 참이 되는 귀무가설에 정반대의 결론이 도출되는 가설을 뜻한다.
즉, 이 두가지 가설을 모집단으로부터 표본을 추출해 분석한 후 채택하거나 기각하는 것을 가설검정이라고 한다.
귀무가설이 채택된다는 뜻은 기존의 개념이 참이고 새로운 가설은 거짓이 되는 것으로 볼 수 있고, 대립가설이 채택된다면 새로운 가설이 참으로 받아들여진다는 뜻이다. 하지만 이렇게 대립가설이 기각된다고 해서 항상 귀무가설이 참이라는 뜻으로 해석해서는 안된다. 만약 새로운 데이터가 쌓이고 이를 분석하게 된다면 귀무가설이 기각되는 경우 또한 발생할 수 있기 때문이다.
예를 들어 스페인 독감은 스페인에서 발병한 질병이라는 귀무가설로, 스페인 독감은 스페인이 발병지가 아니다를 대립가설로 정하였다고 가정한다. 추가적인 데이터 없이 이름만 보았을 때는 이 경우엔 귀무가설이 채택될 수 있다. 하지만 좀 더 정보를 수집해보자. 1차 대전에서 연합국은 적국에 이로운 상황을 알리지 않기 위해 독감 발병에 대해 숨겼고 참전하지 않은 스페인은 언론에서 이를 비교적으로 더 많이 다루게 되어 마치 스페인에서 창궐한 것처럼 보이게 되었다는 것을 알게 된다면 귀무가설을 무작정 채택하기는 힘들 것이다. 이러한 채택에 대한 기준은 p-value로 판단할 수 있다.
1종 오류와 2종 오류
1종 오류와 2종 오류에 대해서 설명을 추가하자면 1종 오류는 귀무가설이 참인데 이를 기각하는 경우, 2종 오류는 귀무가설이 거짓인데 이를 채택하는 경우를 뜻한다. 1종 오류를 범할 확률은 P(H0 기각 | H0 참)을 \( \alpha \)로 P(H0 채택 | H0 거짓)을 \( \beta \)로 둔다.
p-value란 귀무가설이 참이라고 가정했을 때 관측한 값과 같거나 더 극단적인 값이 나올 확률이라 볼 수 있다. 극단적인 값이란 대립가설 방향으로 가는 것을 말한다.
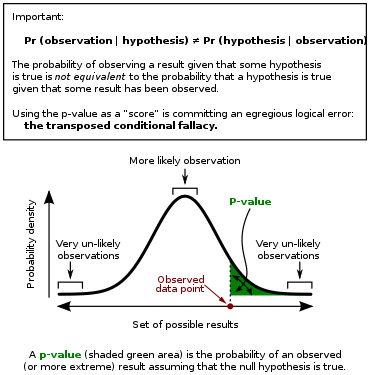
일반적으로 0.05로 설정하는 유의수준 \( \alpha \)보다 p-value(유의확률)값이 크면 귀무가설을 채택하고 p-value가 0.05 이하이면 귀무가설이 기각된다. 유의수준과 유의확률이 헷갈리거나 조금 더 자세한 설명이 필요하다면 여기를 참조 바란다.
- p-value ≤ \( \alpha \) -> 귀무가설(H0) 기각
- p-value >\( \alpha \) -> 귀무가설(H0) 채택
이때, 검정하는 가설의 숫자가 늘어나면 귀무가설이 기각될 확률이 낮더라도 기각될 가능성이 더 늘어나게 된다.
예를 들어 신뢰수준이 95%인 3개의 집단이 있다면, 95% x 95% x 95% = 85.7%이 되어 신뢰수준이 떨어지는 경우가 있다. 또는 암환자와 암에 걸리지 않은 사람의 총 6000개의 유전자 샘플에서 유전자의 활동성을 측정하고 비교한다고 가정한다. 이때 총 6000번의 귀무 가설에 대해 검정하여야 한다. 유의 수준을 0.05로 정한다면 귀무 가설이 기각될 확률은 모두 5%로 동일하지만 6000x0.05=300으로 6000번 중 300번은 참인 귀무가설임에도 불구하고 기각되는 경우가 생긴다.
이러한 귀무가설이 참임에도 불구하고 기각하는 것을 제1종 오류라고 한다. 다시 말해 한 번의 가설검정에서 오류가 발생할 확률을 \( x \)로 두고 유사한 데이터로 가설검정을 여러 번 하면 5\( x \)만큼 오류 발생 확률이 커진다는 것이다.
본페로니 교정(Bonferroni Correction)과 사후 검정(Post-hoc)
위와 같은 오류를 보정하기 위해서 여러 개의 가설들에 대해서 최소한 하나의 제 1종오류가 발생할 가능성 FWER(familywise error rate)을 조절하여 다중 검정을 수행한다. 쉽게 말해 FWER은 하나라도 참인 귀무 가설을 기각할 확률을 뜻한다. 이 FWER은 본페로니 교정(Bonferroni Correction)을 이용해 통제할 수 있다.
ANOVA와 같은 분산 분석의 마지막 단계에는 본페로니 교정과 같은 사후 검정(Post-hoc) 수행이 필요하다. f검정(분산분석)만으로는 t검정을 대체할 수 없다. t검정으로 A, B 집단을 비교할 경우 A,B 집단에 대한 차이를 알 수 있다. 하지만 집단이 A, B, C로 늘어나고 분산분석을 사용했다고 가정하면, 분산분석은 서로 유의차가 있는 어느 두 집단이 존재하는지 '여부'만을 알 수 있다.
예를 들어 세 집단 A, B, C로 분산분석을 했고 p값이 0.05보다 작게 나와서 유의차가 있다. 여기서 유의차가 있다는 말은 '세 집단의 평균이 같지는 않다'는 뜻인데 귀무가설이 A=B=C 이므로, 결국 이 귀무가설은 기각된다. 여기서 우리는 누가 다르다는 것인지에 대해 모호해진다. 이런 의문을 해결하기 위해 사후 검정이 존재한다.
다시 본페로니 교정으로 돌아와 위의 유전자 샘플 예시를 다시 활용하자면, 유의 수준인 0.05를 6000으로 나누는 것이다. 이를 통해 이전 유의 수준에 비해 훨씬 더 기각할 확률이 낮아진다. n개의 독립 혹은 비독립의 가설을 검정할 때 유의확률이 \( x \)라면 \( x \)/n로 낮추어 검정하는 것이다.
즉, 본페로니 교정이란 다중 비교에서 생길 수 있는 오류를 보정하는 방식이다. 하지만 이 본페로니 교정은 실제로 기각되어야 하는 귀무가설도 기각을 하지 않게 되어 검정력을 잃는 오류인 제2종 오류 발생 위험이 있다.
관련 포스트
2022.02.16 - [Data Science/Data Analysis] - [Python] 분산 분석을 위한 ANOVA(Analysis Of Variance)
참고 자료
https://hsm-edu.tistory.com/1165

