DTW(Dynamic Time Warping, 동적 시간 워핑)
DTW(Dynamic Time Warping, 동적 시간 워핑)란 두 개의 시계열이 존재할 때 상호 간 얼마나 유사한지 측정하기 위한 방식이다. 길이가 동일한 시계열의 유사도를 측정하는 방법은 다양하다. 코사인 유사도를 사용해도 되고, 유클리드 거리(Euclidean Distance)를 이용해 계산하면 유사도를 판단할 수 있다. 유클리드 거리는 두 점사이의 거리를 계산할 때 사용하는 방법인데 수식은 아래와 같다.
$$ d = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2+...+(a_n-b_n)^2} $$
유클리드 거리는 계산이 쉽고 연산 속도가 빠르다는 장점이 있다. 하지만 유클리드 거리는 같은 시점의 거리를 계산하기 때문에 속도를 반영할 수 없다. 따라서 동일한 패턴일지라도 속도 혹은 비교 시작점이 다르면 유사도가 크지 않다는 결론을 도출한다. 그러므로 데이터의 길이가 다르거나 신호의 떨림이 커질수록 결과가 기대한 것과 다르게 나온다.
반면 DTW는 길이가 다른 두 시계열의 유사도 또한 측정할 수 있다. 이는 동일 생체 신호의 패턴이 레졸루션이 작을 때와 클 때의 두 데이터가 있는 경우가 될 수 있다.
또한 지연과 같은 이유로 데이터에 shift가 발생했을 때 적용 가능하다. 예를 들어 두 목소리 데이터가 있을 때, 하나는 느리게 말하고 다른 하나는 빠른 속도로 얘기했을 경우가 될 수 있다.
즉, DTW는 다른 속도, 움직임 등을 가진 서로 다른(동일하더라도 여러번 관측된) 신호의 Time 축에 대한 파장의 유사도를 측정할 수 있도록 하는 알고리즘이다. 다만 유클리드 거리 계산 방식에 비해 알고리즘 구현이 복잡하고 연산량이 많다는 단점이 있다.
아래는 유클리드 거리와 DTW의 비교 그래프이다. 유클리드 거리는 각 점들이 1 대 1로 매칭 되지만 DTW는 거리가 짧은 지점을 찾아 시작점을 매칭 한다.

위에서 언급했듯 DTW는 매트릭스의 최단 거리를 찾아간다. 거리가 자장 짧은 시점이 유사도가 높은 시작점이 되고 이 지점을 찾아 계산한다. 아래는 DTW를 좀 더 상세하게 그려 표현한 그림이다.

이번에는 DTW의 의사 코드이다.
int DTWDistance(s: array [1..n], t: array [1..m]) {
DTW := array [0..n, 0..m]
for i := 0 to n
for j := 0 to m
DTW[i, j] := infinity
DTW[0, 0] := 0
for i := 1 to n
for j := 1 to m
cost := d(s[i], t[j])
DTW[i, j] := cost + minimum(DTW[i-1, j ], // insertion
DTW[i , j-1], // deletion
DTW[i-1, j-1]) // match
return DTW[n, m]
}
이번에는 python으로 DTW를 구현한 코드이다. 또한 https://pypi.org/project/dtw/에서 dtw 라이브러리 관련 자료를 볼 수 있다.
import matplotlib.pyplot as plt
import numpy as np
MAX = 999999
def DTW(A, B, window=MAX, d=lambda x, y: abs(x-y)):
# 비용 행렬 초기화
A, B = np.array(A), np.array(B)
M, N = len(A), len(B)
cost = MAX * np.ones((M, N))
# 첫행과 첫열 값 채우기
cost[0, 0] = d(A[0], B[0])
for i in range(1, M):
cost[i, 0] = cost[i - 1, 0] + d(A[i], B[0])
for j in range(1, N):
cost[0, j] = cost[0, j - 1] + d(A[0], B[j])
# 나머지 요소 계산
for i in range(1, M):
for j in range(max(1, i - window), min(N, i + window)):
choices = cost[i - 1, j - 1], cost[i, j - 1], cost[i - 1, j]
cost[i, j] = min(choices) + d(A[i], B[j])
# 최적 경로 산출
n, m = N - 1, M - 1
path = []
while (m, n) != (0, 0):
path.append((m, n))
m, n = min((m - 1, n), (m, n - 1), (m - 1, n - 1), key=lambda x: cost[x[0], x[1]])
path.append((0, 0))
return cost[-1, -1], path
def main():
A = np.array([1, 2, 3, 4, 2, 3])
B = np.array([7, 8, 5, 9, 11, 9])
cost, path = DTW(A, B, window = 6)
print('Total Distance is ', cost)
offset = 5
plt.xlim([-1, max(len(A), len(B)) + 1])
plt.plot(A)
plt.plot(B + offset)
for (x1, x2) in path:
plt.plot([x1, x2], [A[x1], B[x2] + offset])
plt.show()
if __name__ == '__main__':
main()
DTW는 아래 자료들을 토대로 실제로 손으로 계산해보면 좀 더 빨리 이해가 된다.
우선 아래 두 시계열 데이터를 이용해 DTW를 계산을 수행해본다.

1. 비용 행렬 초기화 (6x6의 행렬을 만들고 무한대로 값을 할당)

2. 첫 행과 첫열 값 채우기
(0,0)의 요소는 abs(A-B) 요소의 첫 번째 값의 차로 둔다.
이후 abs(B[:]-A[0])를 수행한 것을 각 1행의 요소들인 (0, 1), (0, 2), (0, 3), (0, 4), (0, 5)에 대입하고,
abs(A[:]-B[0])를 수행한 것을 각 1열의 요소들인 (1, 0), (2, 0), (3, 0), (4, 0), (5, 0)에 대입한다.
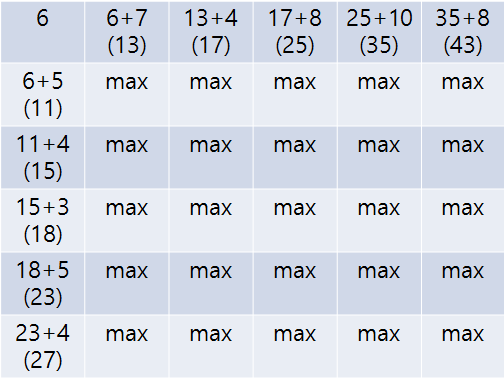
3. 나머지 요소 계산
min(cost[i - 1, j - 1], cost[i, j - 1], cost[i - 1, j])과 A[i], B[j] 의 차의 절댓값을 더한다.
만약 (1, 2)의 값을 구한다면 (0, 1), (0, 2), (1, 1) 중 가장 작은 값인 12와 abs(A[1]-B[2])인 3을 더해 15가 된다.

4. 최적 경로 산출
(5, 5)의 34가 DTW distance가 되고 (4, 5), (4, 4), (5, 4)에 최솟값들을 표시하며 0번째 행으로 진행한다. 이때 만약 (4, 5)가 28이라면 B의 4번째 요소가 A의 4, 5번째 요소에 매칭 되게 된다.
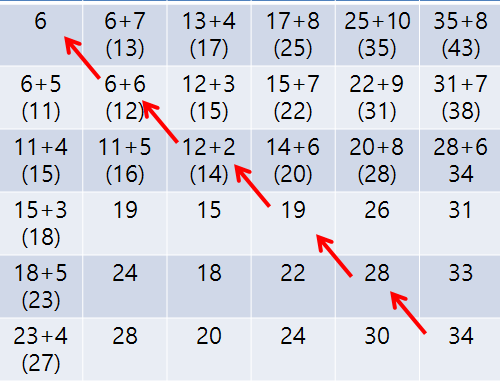
위의 경우처럼 대각선으로 이동한다는 것은 A, B 두 시계열 데이터가 일정하게 변화했다는 의미이다.
아래 파란색 선이 A([1, 2, 3, 4, 2, 3])이고, 주황색 선이 B([7, 8, 5, 9, 11, 9])이다.
만약 (4, 5)가 28이었다면 아래 그래프에서 주황색 선의 x=4일 때, 파란색 선의 x=4인 지점과 x=5인 지점으로 두 개의 선이 연결된다.

관련 포스트
참고 자료
https://en.wikipedia.org/wiki/Dynamic_time_warping
https://hamait.tistory.com/862
소스코드

