주요 개념
두 점 사이의 거리를 구하는 방법은 유사도(Similarity)와 관련이 있다. 거리가 가까울수록 해당 데이터가 가지고 있는 특징(feature)이 유사할 가능성이 크기 때문이다.
두 점사이 거리를 구하기 위한 대표적인 방법으로 아래 세 가지가 있다. 하지만 아래 방식들은 데이터의 차원과 요소 개수가 동일해야 한다.
유클리드 거리(Euclidean Distance)
우선 유클리드 거리(Euclidean Distance)는 아래 그림과 같이 계산할 수 있다.

피타고라스 정리와 크게 다르지 않다. 다만 차수가 많아져도 아래와 같이 계산할 수 있다.
$$ d = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2+...+(a_n-b_n)^2} $$
아래는 수식을 파이썬으로 구현한 것이다.
def euclidean_distance(A, B):
distance = 0
for i in range(len(A)):
distance += (A[i] - B[i]) ** 2
return distance ** 0.5
print(euclidean_distance(A=[1, 5, 7, 9], B=[2, 3, 6, 15]))맨해튼 거리(Manhattan Distance)
다음으로 맨해튼 거리(Manhattan Distance)이다. 이는 택시 거리 또는 시가지 거리로도 불리는데 유클리드 기하학의 거리 공간을 좌표 평면에 표시된 두 점 사이 거리차에 따른 새로운 거리 공간으로 대신하기도 한다. 하지만 유클리드 거리는 차의 제곱을 사용하여 2차원일 때 직선거리를 구하지만, 맨해튼 거리는 차의 절댓값을 바로 더해서 산출하여 마리 맨해튼 거리의 블록들을 지나가는 형태와 유사한 경로가 산출된다.
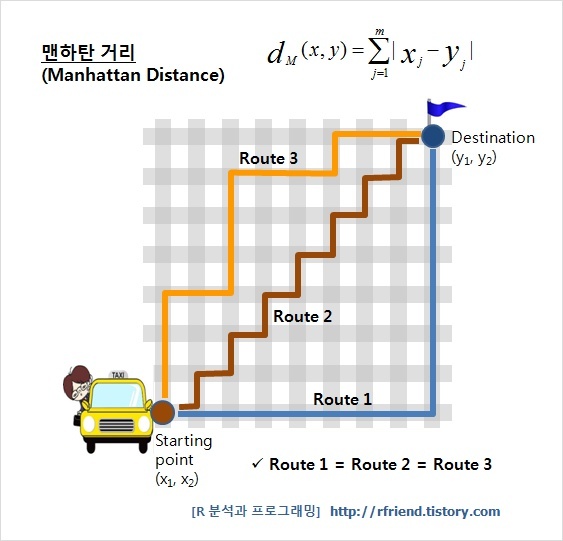
$$ d = |{(a_1-b_1)}|+|{(a_2-b_2)}|+...+|{(a_n-b_n)}| $$
아래는 파이썬으로 구현한 맨하탄 거리이다.
def manhattan_distance(A, B):
distance = 0
for i in range(len(A)):
distance += abs(A[i] - B[i])
return distance
print(manhattan_distance(A=[1, 5, 7, 9], B=[2, 3, 6, 15]))해밍 거리(Hamming Distance)
마지막으로 해밍 거리(Hamming Distance)이다. 해밍 거리는 각 요소마다의 차이가 아닌 정확한지에 대해서만 고려한다. 즉, 같은 길이의 문자열의 같은 위치에서 서로 다른 기호들의 개수를 알 수 있다. 예를 들어 Distance라는 단어가 있을 때 Distttce라고 오타가 났다면 이때 해밍 거리는 2가 된다. 또는 2진수 0011과 1010이 있을 때 해밍 거리는 2가 되는데 이를 이용해 신호학에서 오류 검출 시에도 이용된다. 아래는 파이선 코드이다.
def hamming_distance(A, B):
distance = 0
for i in range(A(pt1)):
if A[i] != B[i]:
distance += 1
return distance
print(hamming_distance([0, 0, 1, 1], [1, 0, 1, 0]))
scipy 라이브러리를 이용하면 더 편하게 구할 수 있다.
from scipy.spatial import distance
print(distance.euclidean([1, 5, 7, 9], [2, 3, 6, 15]))
print(distance.cityblock([1, 5, 7, 9], [2, 3, 6, 15]))
print(distance.hamming([0, 0, 1, 1], [1, 0, 1, 0]))
관련 포스트
2022.02.09 - [Data Science/Data Analysis] - [Python] 길이가 다른 데이터 유사도 측정을 위한 DTW(Dynamic Time Warping)
참고 자료
https://hleecaster.com/ml-distance-formula/

