음성정보처리를 수행할 때 Hidden Markov Model(HMM)에 대해 배우게 된다. 현재는 DNN 기반의 여러 방법들이 사용되고 있지만 레거시라고 그냥 넘어가기엔 큰 영향이 있었던 방법이므로 다시 정리하려한다. HMM을 살펴보기 전 Markov Model이 무엇인지 먼저 살펴보자.
Markov Model
Markov Model은 확률 기반 시퀀스 모델의 시작점으로 볼 수 있다. Markov Model은 시스템이 여러 상태를 가지고 있으며, 각 상태(State) 사이를 이동하는 확률인 전이 확률(Transition Probability)을 마르코프 성질로 정의한 확률 모델을 의미한다. 상태와 전이 확률을 다음과 같이 정의할 수 있다.
- 상태(State): 시스템이 취할 수 있는 다양한 상태.
예) 날씨의 경우 맑음, 흐림, 비, 눈 등 다양한 상태 - 전이 확률(Transition Probability): 한 상태에서 다른 상태로 이동할 확률.
예) 맑음에서 흐림으로 이동할 확률, 흐림에서 비로 이동할 확률 등
이는 마르코프 성질(Markov Property)이라는 중요한 가정을 기반으로 한다. Markov Property란 미래 상태는 현재 상태에만 의존하고, 과거 상태에는 의존하지 않는다는 성질을 의미한다. 예를 들어, 오늘 날씨가 맑다면 내일 날씨가 맑을 확률은 오늘 날씨가 맑다는 사실만으로 결정되고, 지난주 날씨가 어떻든 상관없다는 것이다. 개인적으로 이 부분에 대해 바로 이전 상태(\( t-1 \))가 과거의 모든 정보를 요약하고 있는 것과 같다는 의미로 받아들였을 때 더 와닿았다.
- First-order dependency: 어떤 시점의 상태는 직전 시점의 상태에만 의존하며, 그 이전의 상태에는 독립적이다.
$$ P(q^t = j | q^{t-1} = i, q^{t-2}, ...) = P(q^t = j | q^{t-1} = i) = a_{ij} $$ - Time-invariance: 시불변성은 상태 전이 확률은 시간 \( t \)에 의존하지 않는다. 즉, 상태 간의 전이 확률은 항상 일정하다.
$$ P(q^t = j | q^{t-1} = i) = a_{ij} for all t $$
따라서 Markov Model의 기본 전제는 현재 상태가 주어졌다면, 미래 상태는 과거 상태에 독립적이다를 상정하고 시작한다.
$$ P(X_{t+1} | X_t, X_{t-1}, ..., X_1) = P(X_{t+1} | X_t) $$
이 성질 덕분에 상태 전이가 간단한 확률표 또는 행렬로 표현 가능하다.
마르코프 모델은 시간의 흐름을 따라 확률이 진화하는 모델인 연속 마르코프 체인(Continuous-Time Markov Chain)과 이산 상태공간을 갖는 이산 마르코프 체인(Discrete Markov Chain)이 있다. 연속 마르코프 모델은 확률 미분 방정식 기반으로 동작하여 비교적 수학적으로 난이도가 높으며, 직관적으로 이해하기 어렵기도 하다. 또한 HMM(Hidden Markov Model), MDP(Markov Decision Process) 등 실전 모델은 이산 마르코프 체인을 기반으로 확장되므로 이산 마르코프 체인을 이용하여 예제를 하나 만들어보자.
전체 모델은 다음 세 가지 요소 \( (S, a, \pi) \)로 정의된다.
- 상태 집합: \( S = {s_1, s_2, ..., s_N} \)
- 초기 상태: \( \pi = n \times 1 \text{ initial state probability vector } \left( \sum_i \pi_i = 1 \right) \)
- 전이 확률 행렬: \( a = n \times n \text{ state transition probability matrix } \left( \sum_j a_{ij} = 1 \text{ for all } i \right) \)
만약 상태 집합 \( S \)가 고정된 구조라면 \( \text{Markov Model}\,\theta = (\pi, a) \)로 표현할 수 있다. 여기서 고정된 구조는 모델이 시작되기 전에 상태 목록을 우리가 알고 있고, 그 목록이 바뀌지 않는다는 것을 의미한다.
항아리에 다음과 같이 공 3가지가 들어있다고 가정하자. "RED", "GREEN", "BLUE" 중 하나라고 하자. 각 날씨에 따라 다음 날로의 전이 확률을 다음과 같이 설정할 수 있다. 이 때, 맑은, 흐림, 비 와 같이 상태 집합은 고정되어 있다.

예시 상태 행렬(\( \pi \))
\( \pi \) = \( [s_1, s_2, s_3] \) = [0.5, 0.2, 0.3] = [RED, GREEN, BLUE]
예시 전이 행렬(a)
\[
a =
\begin{bmatrix}
\textcolor{red}{0.4} & \textcolor{green}{0.3} & \textcolor{blue}{0.3} \\
\textcolor{red}{0.2} & \textcolor{green}{0.6} & \textcolor{blue}{0.2} \\
\textcolor{red}{0.1} & \textcolor{green}{0.1} & \textcolor{blue}{0.8}
\end{bmatrix}
\]
이는 현재가 RED일 때 다음 선택이 다시 RED일 확률이 40%임을 의미한다.
Hidden Markov Model(HMM)
위에서 설명한 Markov Model은 모든 상태가 관측 가능하다는 가정 하에 작동한다. 즉, 시스템의 상태 전이가 시간에 따라 확률적으로 이루어지며, 그 상태를 직접 관찰할 수 있다고 본다.
그러나 현실 세계의 많은 문제에서는, 실제 상태(state)는 직접 관측할 수 없고, 대신 그 상태에서 발생한 관측 결과(observation)만을 알 수 있는 경우가 많다. 예를 들어, 사람의 감정 상태는 직접 보이지 않지만 음성, 표정, 언어 등을 통해 간접적으로 관측할 수 있다. 따라서 HMM의 가장 핵심적인 특징은 상태(state)가 직접 관측되지 않는다는 것이다. 대신, 각 상태에서 확률적으로 관측값(observation)이 발생한다. 이 때, 상태 시퀀스는 숨겨져 있으며 \( q^{1:T} = (q^1, q^2, \dots, q^T) \)로 표현된다. HMM의 Property는 다음과 같이 정리할 수 있다.
- First-order dependency: 어떤 시점의 상태는 직전 시점의 상태에만 의존하며, 그 이전의 상태에는 독립적이다.
$$ P(q^t = j | q^{t-1} = i, q^{t-2}, ...) = P(q^t = j | q^{t-1} = i) = a_{ij} $$ - Time-invariance: 시불변성은 상태 전이 확률은 시간 \( t \)에 의존하지 않는다. 즉, 상태 간의 전이 확률은 항상 일정하다.
$$ P(q^t = j | q^{t-1} = i) = a_{ij} for all t $$ - 주어진 \( \text{Observation sequence: } x^{1:T} = (x^1, x^2, \dots, x^T) \)에 따라 Unobservable state sequence가 도출됨.
$$ \text{Unobservable state sequence: } q^{1:T} = (q^1, q^2, \dots, q^T) $$
이처럼 상태는 숨겨져(hidden) 있고, 우리는 초기 상태 확률, 상태 전이 확률, 관측 확률(Observation Probability)를 바탕으로 숨겨진 상태의 시퀀스를 추정해야 한다. 이러한 구조를 가진 모델이 바로 Hidden Markov Model(HMM)이다.
다음은 HMM의 요소들을 가지고 있다.
- 상태 집합: \( S = {s_1, s_2, ..., s_N} \)
- 초기 상태: \( \pi = n \times 1 \text{ initial state probability vector } \left( \sum_i \pi_i = 1 \right) \)
- 전이 확률 행렬: \( a = n \times n \text{ state transition probability matrix } \left( \sum_j a_{ij} = 1 \text{ for all } i \right) \)
- 관측 확률 행렬: \( b = n \times v \text{ observation(emission) probability matrix } \left( \sum_j b_{ij} = 1 \text{ for all } i \right) \)
따라서 상태 집합 \( S \)가 고정된 구조일 때, \( \text{HMM}\,\theta = (\pi, a, b) \)과 같이 표현될 수 있다. 위와 동일한 수치를 이용하여 예시를 다음과 같이 만들어보자.
예시 상태 행렬(\( \pi \))
\( \pi \) = \( [s_1, s_2, s_3] \) = [0.5, 0.2, 0.3] = [RED, GREEN, BLUE]
예시 전이 행렬(a)
\[
a =
\begin{bmatrix}
{0.4} & {0.3} & {0.3} \\
{0.2} & {0.6} & {0.2} \\
{0.1} & {0.1} & {0.8}
\end{bmatrix}
\]
예시 관측 행렬(b)
\[
b =
\begin{bmatrix}
\textcolor{red}{0.2} & \textcolor{green}{0.3} & \textcolor{blue}{0.5} \\
\textcolor{red}{0.3} & \textcolor{green}{0.4} & \textcolor{blue}{0.3} \\
\textcolor{red}{0.6} & \textcolor{green}{0.3} & \textcolor{blue}{0.1}
\end{bmatrix}
\]
이 때, 다음과 같은 상황이 있다고 가정하자.
- 관측 시퀀스: \( x^{1:4} = [\text{red}, \text{red}, \text{blue}, \text{blue}] \)
→ b 행렬: 상태가 색깔을 방출할 확률로 색깔과 직접 관련이 있음 - 숨겨진 상태 시퀀스: \( q^{1:4} = [s_1, s_2, s_2, s_3] \)
→ a행렬: 상태 간 이동 확률이므로 색깔과 무관함. - 공동 확률: \( P(x^{1:4}, q^{1:4} \mid \theta) \)
위 예제를 계산하면 다음과 같다.
\[
\begin{aligned}
P(x^{1:4}, q^{1:4} \mid \theta)
&= \pi_1 \cdot b_{11} \cdot a_{12} \cdot b_{21} \cdot a_{22} \cdot b_{23} \cdot a_{23} \cdot b_{33} \\
&= 0.5 \times 0.2 \times 0.3 \times 0.3 \times 0.6 \times 0.3 \times 0.2 \times 0.1 \\
&= 0.0000324
\end{aligned}
\]
이 예시는 관측 시퀀스와 상태 시퀀스가 주어졌을 때 Joint Likelihood를 계산하는 방식이며, 전체 \( P(x∣\theta) \)는 모든 가능한 상태 시퀀스에 대해 위 값을 합산해야 하므로 일반적으로 Forward 알고리즘을 사용한다.
Likelihood는 관측된 데이터를 바탕으로, 어떤 모델이 그 데이터를 설명하는 데 가장 적합한지를 판단하기 위해 사용한다. HMM은 이 최대 Likelihood를 찾아 나가는 방향으로 진행된다. 이 과정은 Forward, Backward, Baum-Welch Algorithm을 사용하여 최종 결과까지 도출한다.
Forward Algorithm
Forward Algorithm은 시간 \( t \)까지의 부분 관측 시퀀스를 고려하여, 상태 \( s_j \)에 있을 누적 확률을 재귀적으로 계산한다. 즉, 시간 \( t \)까지의 관측 시퀀스 \( x^1, x^2, ..., x^t \)를 생성하고, 그 시점에 상태 \(j \)에 있을 확률이다.

$$ \alpha_t(j) \equiv P(x^1, x^2, \cdots, x^t, q^t = j \mid \theta) = \sum_{q^{1:t-1}} P(x^1, x^2, \cdots, x^t, q^1, q^2, \cdots, q^{t-1}, q^t = j \mid \theta) $$
Backward Algorithm
Backward Algorithm은 Forward와 반대로, 현재 상태에서 남은 관측 시퀀스를 생성할 확률을 계산한다. 또한 Baum-Welch 알고리즘에서 사용된다. 즉, 상태 \( i \)에서 시작하여, 시간 \( t+1 \)부터 \( T \)까지의 관측값을 생성할 모든 상태 경로에 대한 총합이다.

$$ \beta_t(i) \equiv P(x^{t+1}, x^{t+2}, \cdots, x^T \mid q^t = i, \theta) = \sum_{q^{t+1:T}} P(x^{t+1}, \cdots, x^T, q^{t+1}, \cdots, q^T \mid q^t = i, \theta) $$
Baum-Welch Algorithm
Baum-Welch Algorithm은 Maximum Likelihood Estimation(MLE)을 수행하는 알고리즘이다. Expectation-Maximization(EM) 알고리즘의 구조를 따른다. Expectation Step(E-Step)과 Maximization(M-Step)이 있는데 하나씩 알아보자.
Expectation Step(E-Step)
먼저 Expectation Step(E-Step)에선 \( \gamma \)와 \( \xi \)가 도출된다.
$$ Q(\hat{\theta} \mid \theta) \equiv \mathbb{E}_{q^{1:T}} \left[ \log P(x^{1:T}, q^{1:T} \mid \hat{\theta}) \mid x^{1:T}, \theta \right] $$
여기서 Q는 Baum’s 𝑄 function인데 간단하게 설명하자면 숨겨진 정보를 고려해 파라미터를 개선하는 핵심 수식이다.
$$ Q(\hat{\theta} \mid \theta) = \mathbb{E}_{q^{1:T} \sim P(q^{1:T} \mid x^{1:T}, \theta)} \left[ \log P(x^{1:T}, q^{1:T} \mid \hat{\theta}) \right] $$
상태 점유 확률(\( \gamma_t(i) \))
\( \gamma_t(i) \)는 시점 \( t \)에서 상태 \( i \)에 있을 사후 확률(posterior probability)을 도출한다.

$$ \gamma_t(i) \equiv P(q^t = i \mid x^1, x^2, \cdots, x^T, \theta) $$
$$ \gamma_t(i) = \frac{\alpha_t(i) \cdot \beta_t(i)}{\sum_i \alpha_t(i) \cdot \beta_t(i)} $$
상태 전이 점유 확률(\( \xi_t(i, j) \))
\( \xi_t(i, j) \)는 시간 \( t \)에 상태 \( i \)에 있고, 시간 \( t+1 \)에 상태 \( j \)로 전이(arc)되었을 사후 확률(posterior probability)을 나타낸다.
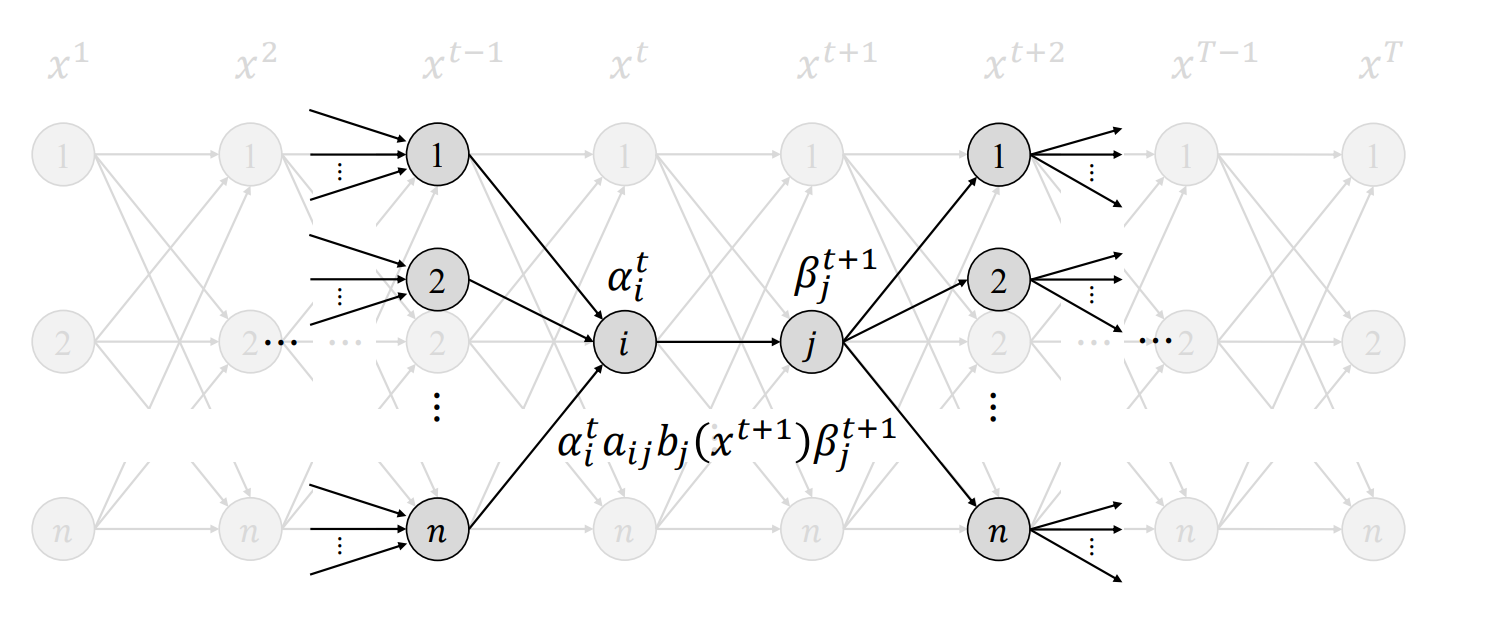
$$ \xi_t(i, j) \equiv P(q^t = i, q^{t+1} = j \mid x^1, x^2, \cdots, x^T, \theta) $$
$$ \xi_t(i, j) = \frac{\alpha_t(i) \cdot a_{ij} \cdot b_j(x^{t+1}) \cdot \beta_{t+1}(j)}{\sum_i \sum_j \alpha_t(i) \cdot a_{ij} \cdot b_j(x^{t+1}) \cdot \beta_{t+1}(j)} $$
Maximization(M-Step)
위에서 계산한 \( \gamma \)와 \( \xi \)를 바탕으로 파라미터를 업데이트한다.
$$ \hat{\theta} = \arg\max_{\hat{\theta}} Q(\hat{\theta} \mid \theta) $$
상태 점유 확률(\( \gamma_t(i) \))
$$ \gamma_t(i) = \frac{\alpha_t(i) \cdot \beta_t(i)}{\sum_{k=1}^N \alpha_t(k) \cdot \beta_t(k)} $$
상태 전이 점유 확률(\( \xi_t(i, j) \))
$$ \xi_t(i, j) = \frac{\alpha_t(i) \cdot a_{ij} \cdot b_j(x^{t+1}) \cdot \beta_{t+1}(j)}{\sum_{i=1}^N \sum_{j=1}^N \alpha_t(i) \cdot a_{ij} \cdot b_j(x^{t+1}) \cdot \beta_{t+1}(j)} $$
초기 상태 확률 업데이트
$$ \pi_i^{\text{new}} = \gamma_1(i) $$
전이 확률 업데이트
$$ a_{ij}^{\text{new}} = \frac{\sum_{t=1}^{T-1} \xi_t(i, j)}{\sum_{t=1}^{T-1} \gamma_t(i)} $$
출력(관측) 확률 업데이트
$$ b_j^{\text{new}}(k) = \frac{\sum_{t=1}^T \delta(x^t = v_k) \cdot \gamma_t(j)}{\sum_{t=1}^T \gamma_t(j)} $$
정리하자면 Baum-Welch 알고리즘은 반복적인 알고리즘으로, 현재 모델 파라미터 \( \theta \)를 기준으로 상태 점유 확률을 추정하는 E-step과 추정된 정보를 바탕으로 파라미터를 최적화하는 M-step을 번갈아 수행한다.
관련 포스팅
참고 자료
고려대학교 육동석 교수님 [AAA605] 음성정보처리 강의자료
https://incodom.kr/%EA%B8%B0%EA%B3%84%ED%95%99%EC%8A%B5/markov_model
https://en.wikipedia.org/wiki/Markov_model

