공분산(Covariance)과 상관 계수(Correlation Coefficient)는 통계학, 데이터 분석, 머신러닝, 금융, 경제학 등에서 널리 사용되고 있다. 대표적으로 데이터 분석 분야에선 변수 간의 관계를 분석하여 데이터의 패턴을 파악하는 데 활용된다. 뿐만 아니라 피처 선택(Feature Selection)에서 상관성이 높은 변수 중 일부를 제거하여 다중공선성 문제를 방지할 때 사용된다. 현재 관심 분야인 신호 처리 및 공학 분야에선 센서 데이터 분석에서 여러 신호 간의 관계를 파악하거나 이미지 및 음성 처리에서도 변수 간의 연관성을 분석할 때 활용된다.
공분산(Covariance)
공분산에 대해 설명하기 전 분산(Variance)에 대해 간단히 짚고 넘어가야 한다. 분산이란 내가 가진 데이터가 평균값을 중심으로 퍼져 있는 평균적인 거리를 표현해 줄 수 있다. 분산의 수식은 아래와 같다.
$$ \text{Var(x)} = \ \sigma^2_X = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 $$
공분산은 두 변수의 평균값을 중심으로 퍼져 있는 평균적인 거리를 의미한다. 수식은 아래와 같다.
$$ \text{Cov(x, y)} = \ \sigma_{XY} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) $$
분모를 여기선 \( n-1 \)으로 설정하였는데 보통 표본 분산과 표본 공분산을 계산하는 경우엔 \( n-1 \)로 분모를 두기 때문이다. 전체 모집단의 분산과 공분산에 대해 도출할 때는 분모를 \( n \)으로 둔다.
분산과 공분산 수식을 놓고 보면 분자 부분이 \( (x_i - \bar{x})^2 \)와 \( (x_i - \bar{x})(y_i - \bar{y}) \)라는 차이만 있다. 좌표 평면으로 옮겨놓고 보면 아래와 같을 것이다. 개인적으로 가장 직관적으로 이해할 수 있는 그림이라고 생각한다.
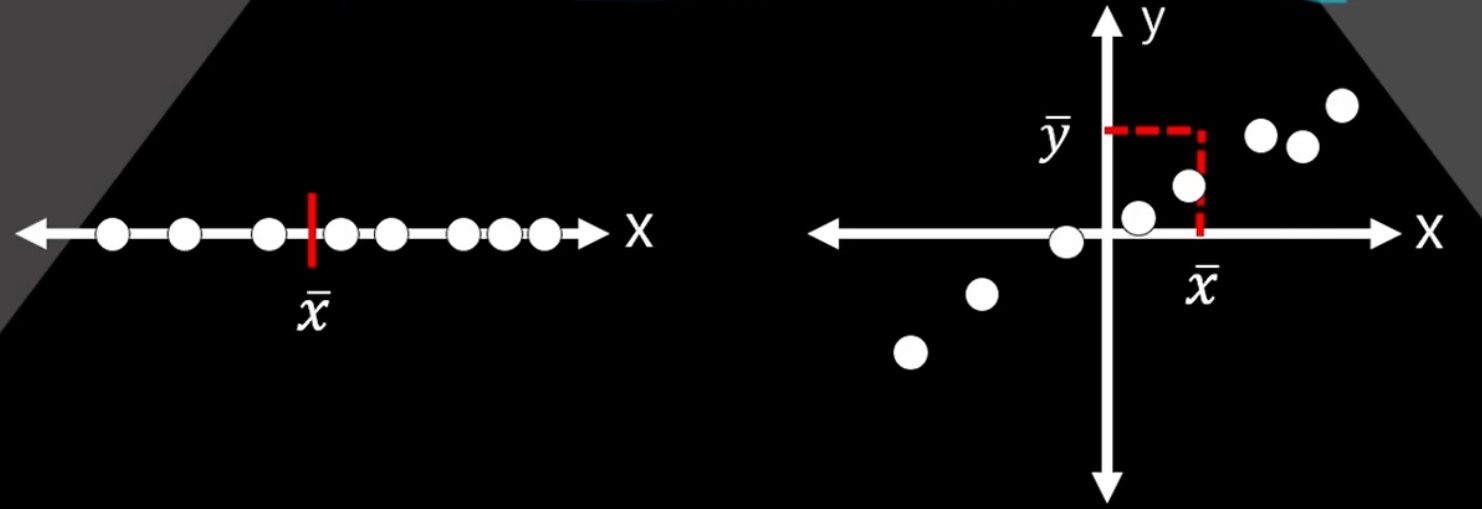
결국 분산은 한 가지 변수의 데이터가 평균에서 얼마나 퍼져있는가에 대한 수치이고, 공분산은 2개 이상 다중 변수의 평균값을 중심으로 얼마나 퍼져있는가에 대한 수치이다. 참고로 2개 이상의 변수는 공변량이라 부른다.
이 공분산은 두 변수 간의 관계를 측정하는 값인데, 만약 두 변수의 변화가 서로 독립적인 경우 공분산은 0이 된다. 예를 들어, 학생들의 수학 점수와 음악 감상 시간을 공분산으로 표현해 보자. 이 두 변수는 일반적으로 큰 상관관계가 없다고 가정할 수 있다.
학생 5명의 수학 점수와 하루 평균 음악 감상 시간을 다음과 같이 가정한다.
- X(수학 점수): [85, 90, 75, 80, 95]
- Y(음악 감상 시간, 단위: 시간): [2, 1, 3, 4, 2]
공분산 수식에 대입하여 계산하면 아래와 같다.
$$ \bar{X} = \frac{85 + 90 + 75 + 80 + 95}{5} = 85 $$
$$ \bar{Y} = \frac{2 + 1 + 3 + 4 + 2}{5} = 2.4 $$
$$ \text{X 편차 계산: } X - \bar{X} = [0, 5, -10, -5, 10] $$
$$ \text{Y 편차 계산: } Y - \bar{Y} = [-0.4, -1.4, 0.6, 1.6, -0.4] $$
$$ \text{곱 계산:} \quad (X - \bar{X}) \times (Y - \bar{Y}) $$
$$ = [0 \times -0.4, 5 \times -1.4, -10 \times 0.6, -5 \times 1.6, 10 \times -0.4] $$
$$ = [0, -7, -6, -8, -4] $$
$$ \quad \text{Cov}(X, Y) = \frac{1}{5} \sum [0, -7, -6, -8, -4] = \frac{-25}{5} = -5 $$
따라서 공분산 값이 -5로 작고, 음수임을 확인할 수 있다. 이는 약간의 역상관이 있을 가능성을 보여주지만, 이 값이 크지 않으므로 \( X \)와 \( Y \) 사이에는 실질적인 상관관계가 거의 없다고 결론 내릴 수 있다.
그렇다면 공분산이 어느 정도 되어야 상관관계가 있다고 할 수 있는 걸까? 사실 공분산 자체는 상관관계를 판단하기 위한 절대적인 기준으로 사용되기 어렵다. 공분산은 각 변수들 간의 관계가 양의 상관관계인지 음의 상관관계인지 정도만 반영하고 있으며 얼마나 크게 상관이 있는지는 알 수 없기 때문이다. 다시 말해 공분산 값이 변수들의 스케일(단위)에 따라 달라지기 때문이다. 따라서 두 변수 간 관계를 판단하기 위해서는 상관계수(Correlation Coefficient)를 사용하는 것이 더 적절하다.
상관 계수(Correlation Coefficient)
공분산(\(Cov(X, Y)\))은 두 변수의 관계의 방향성과 크기를 나타내는 수치였다. 단위가 변수의 단위에 따라 달라지므로, 값을 비교하기 어렵다. 반면 상관 계수(\(r\))는 공분산을 표준화한 값으로, 두 변수 간의 상관관계를 -1에서 1 사이의 값으로 표현한다. 상관계수는 단위와 무관하며, 직접적으로 상관성을 판단할 수 있다. 상관 계수의 수식은 아래와 같다.
$$ r = \frac{\text{Cov}(X, Y)}{\sigma_X \cdot \sigma_Y} $$
- \( \sigma_X\) : \(X\)의 표준편차
- \( \sigma_Y\) : \(Y\)의 표준편차
상관계수는 다음과 같이 해석할 수 있다.
- \( r = 1 \): 완벽한 양의 상관관계. \( X\)가 증가하면 \( Y \)도 항상 일정 비율로 증가)
- \( r = -1 \): 완벽한 음의 상관관계. \( X \)가 증가하면 \( Y \)가 항상 일정 비율로 감소)
- \( r = 0 \): 두 변수 간에 상관관계가 없음
\( \left| r \right| \)의 크기에 따른 해석:
\begin{cases}
0.0 \leq \left| r \right| < 0.3 & : \text{거의 상관관계가 없음} \\
0.3 \leq \left| r \right| < 0.7 & : \text{약한 상관관계} \\
0.7 \leq \left| r \right| < 1.0 & : \text{강한 상관관계}
\end{cases}
위의 예제인 수학 점수와 음악 감상 시간을 사용해 상관계수를 계산해 보자. 위 공분산에서 도출된 값인 \( Cov(X, Y) = -5 \)를 가져와 아래 표준 편차를 도출하는데 사용하면 된다.
- X(수학 점수): [85, 90, 75, 80, 95]
- Y(음악 감상 시간, 단위: 시간): [2, 1, 3, 4, 2]
$$ \text{X 편차 계산: } X - \bar{X} = [0, 5, -10, -5, 10] $$
$$ \text{Y 편차 계산: } Y - \bar{Y} = [-0.4, -1.4, 0.6, 1.6, -0.4] $$
$$ \sigma_X = \sqrt{\frac{1}{n} \sum (X - \bar{X})^2} = \sqrt{\frac{1}{5} (0^2 + 5^2 + (-10)^2 + (-5)^2 + 10^2)} \approx 7.07 $$
$$ \sigma_Y = \sqrt{\frac{1}{n} \sum (Y - \bar{Y})^2} = \sqrt{\frac{1}{5} ((-0.4)^2 + (-1.4)^2 + 0.6^2 + 1.6^2 + (-0.4)^2)} \approx 1.02 $$
$$ r = \frac{-5}{7.07 \times 1.02} \approx -0.69 $$
즉 \( r \approx -0.69 \)로 두 변수 간에 약간 강한 음의 상관관계가 있음을 의미한다. 이는 \( X \)가 증가할수록 \( Y \)가 감소하는 경향이 있음을 나타낸다.
공분산만 보고 아까는 연관이 크지 않을거라고 판단하였는데 상관계수로 살펴보니 비교적 큰 연관관계가 있다고 나오는 것 아닌가라는 의문이 들 수 있다.
이는 공분산과 상관계수의 스케일과 해석 방식의 차이 때문이다. 수학 점수와 음악 감상 시간은 수치적으로 큰 차이가 나고 있는 데이터이다. 앞서 언급한 것처럼 공분산 값은 변수의 단위와 크기에 따라 달라진다. 두 변수의 관계가 얼마나 강한지 알 수 있지만, 값의 절대적인 크기를 해석하기 어렵다. 상관 계수는 공분산을 두 변수의 표준편차로 나누어 단위의 영향을 제거하였고 \( r \)은 -1~1 사이로 표준화되어 두 변수 간 관계를 명확히 해석할 수 있게 해 준다.
결론적으로 공분산에서 도출된 대로 두 변수 간의 방향성(-5: 음의 방향)에 대해서 판단이 가능하였고, 상관 계수를 도출하여 얼마나 크게 두 변수가 상관관계의 강도(강도: -0.69)를 가지고 있는지 판단할 수 있었다.
공부할 시간에 노래 들으면 집중이 안되거나 딴짓을 할 수 있으니 이치에 맞는 것 같기도 하다. 저 두 데이터가 어떠한 이유로 강한 음의 상관관계를 띄게 하였는지 알아내는 것도 연구자의 몫이기도 하다.
관련 포스팅
2024.04.10 - [Data Science/Data Analysis] - 상관관계(correlation)와 인과관계(causation)
참고 자료

