데이터가 가진 특성에 대해 판단할 때 대표적으로 평균(mean), 중앙값(median), 최빈값(mode) 등을 이용하여 추정할 수 있다. 각 방법은 아래와 같은 특징들이 있다.
평균(mean)
- 산술 평균, 기하 평균, 조화 평균 등의 방식이 있다.
- 변수의 관찰값들을 모두 계산한 것이므로 대푯값으로 바람직하다.
- 추상적인 의미를 가진다.
- 특이값의 영향을 받는 단점이 있다.
중앙값(median), 최빈값(mode)
- 특이값의 영향을 받지 않는다.
- 중앙값은 데이터를 크기순서로 정리해야 하는 불편함이 있다.
- 최빈값은 데이터가 적거나 복잡하면 구할 수 없다.
이번 포스트에선 평균에 대해 더 자세히 알아보려 한다.
산술 평균(Arithmetic mean)
산술 평균(Arithmetic mean)은 우리가 알고 있는 가장 보편적인 평균을 구하는 방식이다. 합의 평균이라 볼 수 있다.
$$ A = \frac{1}{n}\sum_{i=1}^{n}a_i = \frac{a_1 + a_2 + ... + a_n}{n} $$ $$ e.g. \frac{a+b}{2} $$
산술평균은 단순하고 직관적이기는 하다. 다만 우리가 데이터의 중심에 해당하는 것을 평균이라고 생각하기엔 산술 평균은 허점이 있다. 만약 데이터의 가우시안 분포처럼 고르게 나와 대칭을 이루고 있다면 우리가 원하는 결과를 산술평균으로부터 얻게 될 것이다. 하지만 대칭이 아닌 경우 산술 평균이 좋은 방법이 아닐 수 있다. 그러므로 데이터의 평균을 말할 때 해당 데이터의 분포도 함께 고려하여 적절한 방법으로 분석할 필요가 있다.
기하 평균(Geometic mean, Gmean)
산술평균은 합의 평균이라면 기하 평균(Geometic mean, Gmean)은 곱의 평균이다. 산술평균이 전부 더해서 n으로 나눠준다면 기하평균은 전부 곱해서 n으로 제곱근을 통해 구할 수 있다. 주로 연평균성장률, 연평균부채증가율과 같은 비율의 평균을 구할 때 기하 평균을 사용한다.
$$ G = \sqrt[n]{\prod_{i=1}^{n}a_i} = \sqrt[n]{a_1a_2 ... a_{n-1}a_n} $$
예를 들어 3이 6으로 바뀌면 2배 증가한 것이고, 6이 48로 바뀌면 8배 증가한 것인데(3 => 6 => 48) 이런 증가의 기하 평균은 아래와 같다.
$$ r_1r_2 = 2*8 $$ $$ e.g. \sqrt{2*8} = 4 $$
여기서 나온 4를 초기값 3에 두 번 곱하면 \(3*4^2 = 48\)이 된다. 만약 이를 산술평균으로 구했다면 \(\frac{2+8}{2} = 5\)가 되고 초기값 3에 곱하면 \(3*5^2 = 75\)가 나와 최종 도출된 값이 다르게 된다.

곱의 평균을 기하 평균이라고 부르는 이유는 기하의 비례식에서 유래하였기 때문이다. 위 반원에서 직각 삼각형의 닮음식은 아래와 같다.
$$ a : p = p : b $$
여기서 p 가 a, b의 기하 평균이다. 또 다른 예로, 변의 길이가 \(a\)와 \(b\)인 직사각형과 넓이가 같은 정사각형의 한 변의 길이는 \(\sqrt{ab}\)이다. 중고등학교 때쯤 배웠던 산술기하평균도 이런 식으로 도출된 것이다.
$$ a>0, b>0일 때, $$ $$ \frac{a+b}{2}>0\sqrt{ab}이다. $$ $$ (단, 등호는 a=b일 때 성립한다.)$$
쉬어가는 시간으로 산술기하평균 문제도 하나 적어두었다. 답은 안 가르쳐 줄 거다.
- 문제 1. \(x > 1\) 일 때 \(x + 2 + \frac{7}{x-1}\)의 최솟값을 구하시오.
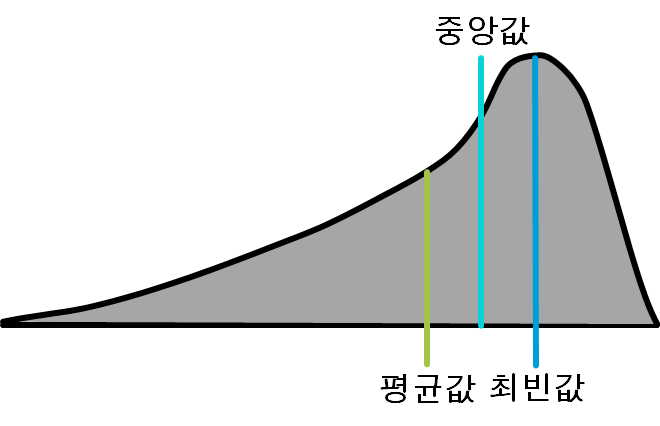
확률변수 X가 어떤 현상의 관측이라고 정의한다면 초반에는 급격하게 많이 등장했다가 X가 증가할수록 어떤 현상 관측 확률이 기하급수적으로 낮아지는 분포를 갖는 스타일의 분포를 기하분포라고 한다. 이런 분포는 오른쪽 꼬리 분포라 불리며 아래와 같은 특징을 가진다.

- 조화 평균 <= 기하 평균 <= 산술 평균
- 최빈값 <= 중앙값 <= 평균값
반대로 왼쪽 꼬리 분포도 존재한다.
- 산술 평균 <= 기하 평균 <= 조화 평균
- 평균값 <= 중앙값 <= 최빈값
아래는 python을 이용하여 각 평균 도출 방식에 적합한 샘플 데이터의 정규 분포를 그려보았다. 이 예제에서 기하 평균을 위한 데이터는 오른 꼬리 분포 형태를 띠는 데이터이다.
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
# Arithmetic mean
arithmetic_x_values = np.linspace(1, 10, 100)
arithmetic_mean = np.mean(arithmetic_x_values)
arithmetic_std = np.std(arithmetic_x_values)
# Geometric mean
np.random.seed(42)
alpha = 1
beta = 5
mode = 0.8
geometric_x_values = np.random.beta(alpha, beta, size=1000)
geometric_mean = np.mean(geometric_x_values)
geometric_std = np.std(geometric_x_values)
# Plotting
plt.figure(figsize=(10, 6))
# Plot normal distribution for Arithmetic
plt.subplot(1, 2, 1)
plt.hist(arithmetic_x_values, bins=20, density=True, alpha=0.6, color='blue')
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, arithmetic_mean, arithmetic_std)
plt.plot(x, p, 'k', linewidth=2)
plt.title('Normal Distribution for Arithmetic mean Data')
plt.xlabel('Value')
plt.ylabel('Density')
# Plot normal distribution for Geometric
plt.subplot(1, 2, 2)
plt.hist(geometric_x_values, bins=20, density=True, alpha=0.6, color='orange')
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, geometric_mean, geometric_std)
plt.plot(x, p, 'k', linewidth=2)
plt.title('Normal Distribution for Geometric mean Data')
plt.xlabel('Value')
plt.ylabel('Density')
plt.tight_layout()
plt.show()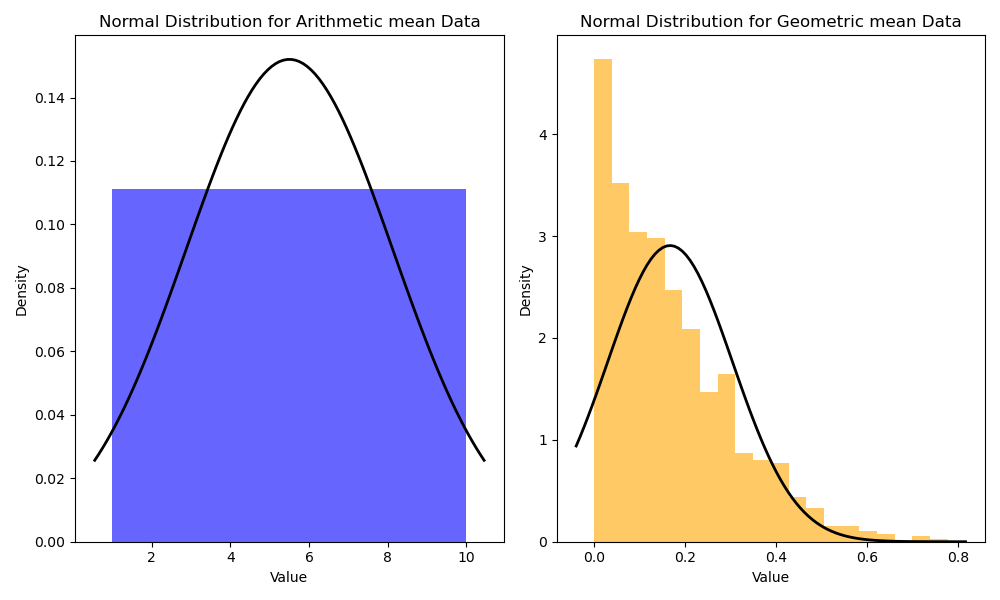
참고로 코드에서 기하 평균을 구할 때 요소 중 0이 하나라도 포함된다면 결과로 0을 반환할 수 있으니 주의하여야 한다.
조화 평균(Harmonic mean)
조화 평균(Harmonic mean)은 '역수의 산술평균의 역수'이다. 역수의 차원에서 평균을 구하고, 다시 역수를 취해 원래 차원의 값으로 돌아오는 것이다. 쉽게 말해 조화 평균은 평균적인 변화율을 구할 때 사용된다.
$$ H = \frac{n}{\sum_{i=1}^{n}\frac{1}{a_i}} = \frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + ... + \frac{1}{n}} $$
또한 조화 평균은 산술 평균과 기하 평균에 대해 아래의 관계식이 성립한다.
$$ H = \frac{G^2}{A} $$
예시를 통해 좀 더 자세히 알아보자.
여기 10km 레이싱 트랙을 도는 자동차가 있다. 시속 100km로 처음 한 바퀴를 돌고, 두 번째는 시속 80km로 완주하였다. 이때 2바퀴를 도는 동안의 조화 평균을 통해 구한 평균 속도는 \(\frac{10}{100}+\frac{10}{80} = 0.225\)이므로 \(\frac{1+1}{0.225} = 88.9km/h\)이다. 산술 평균으로 값을 도출한다면 \(90km/h\)일 것이다. 이 경우는 비교 대상의 측정단위(km/h)가 같은 경우이다. 조화 평균은 비교 대상의 측정 단위가 다를 때 또는 서로 역수의 관계일 때도 사용 가능하다.
조화 평균은 데이터의 클래스가 불균형할 때 클래스가 적은 부분에 더 많은 가중치를 두어 최대한 대등한 관계에 두면서 평균을 구해주게 되기 때문에 Acurracy보다는 F1-score가 더 정확한 성능평가 지표로써 많이 활용된다.
관련 포스트
참고 자료
https://ko.wikipedia.org/wiki/%EC%A1%B0%ED%99%94_%ED%8F%89%EA%B7%A0
https://ko.wikipedia.org/wiki/%EA%B8%B0%ED%95%98_%ED%8F%89%EA%B7%A0
https://bhsmath.tistory.com/265
https://stat-university.tistory.com/entry/%ED%8F%89%EA%B7%A0%EC%97%90-%EB%8C%80%ED%95%9C-%EC%9D%B4%EC%95%BC%EA%B8%B0%EC%82%B0%EC%88%A0%ED%8F%89%EA%B7%A0-%EC%A1%B0%ED%99%94%ED%8F%89%EA%B7%A0-%EA%B8%B0%ED%95%98%ED%8F%89%EA%B7%A0
https://www.beusable.net/blog/?p=3855
https://freedata.tistory.com/21

