머신러닝과 딥러닝에서 모델의 성능을 개선하고 일반화 능력을 높이기 위해 흔히 정규화 기법을 사용한다고 말한다. 여기서 정규화는 크게 Regularization과 Normalization으로 나뉘는데, 두 개념은 서로 다른 목적과 방식으로 적용된다. 하나의 명칭으로 해석되어 혼란스러울 때가 있어 이번에 정리해보려 한다.
Regularization
Regularization은 모델의 복잡도를 제어하여 과적합(Overfitting)을 방지하는 데 사용된다. 모델의 가중치(Weight)에 제약 조건을 추가하여 학습된 모델이 새로운 데이터에 대해서도 잘 일반화할 수 있게 한다.
주요 특징
- 가중치 규제
- 과적합 방지
- 모델 일반화
Regularization 방식에는 대표적으로 L1 정규화(Lasso)와 L2 정규화(Ridge)가 있다.
L1 정규화와 Lasso Regression
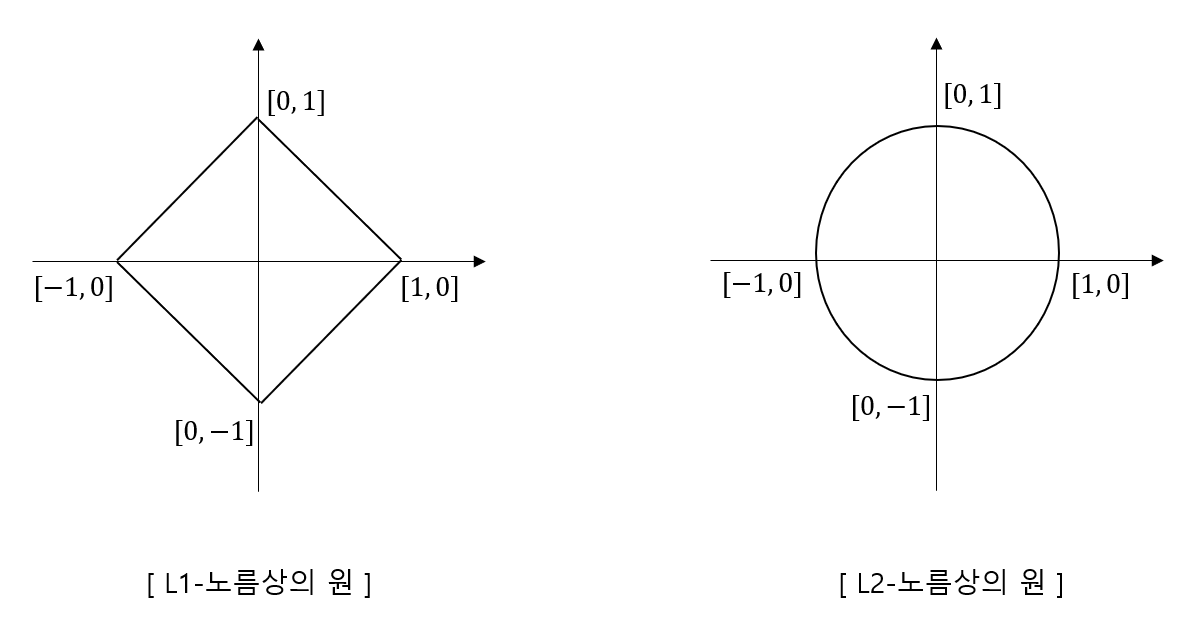
L1 정규화는 비용 함수에 L1 norm(Mahattan Distance)을 가중치 제약으로 추가하여 과적합을 방지하는 기법이다. L1 Norm은 벡터의 각 요소의 절대값 합으로 정의된다.
$$ \|w\|_1 = \sum_{i=1}^{n} |w_i| $$
예를 들어 \( w = (3, 4) \)가 있을 때 아래와 같이 계산된다.
$$ \|w\|_1 = |3| + |-4| = 3 + 4 = 7 $$
이는 벡터의 크기를 계산하는 한 방법으로, 벡터의 희소성(sparsity)을 측정하는 데 유용하다.
위 수식에서 보여지는 것처럼 L1 정규화는 가중치의 절대값 합을 최소화하는 방향으로 나아간다. 또한 선형 회귀 모델에서 L1 규제를 주는 것을 Lasso Regression이라고 한다.
손실 함수와 비용 함수는 다음과 같이 정의된다.
$$ Loss(w) = \sum_{i=0}^{N} \left( y_i - \sum_{j=0}^{M} x_{ij} w_j \right)^2 $$
$$ Cost = \text{Loss}(w) + \lambda \sum_{i=1}^{n} |w_i| $$
여기서 \( \lambda \)는 정규화 강도를 조절하는 하이퍼파라미터로 모델의 가중치를 제약해 특정 가중치를 0으로 만들어 희소성을 유도한다.
일부 가중치가 0으로 수렴하게 되면 특성 선택(Feature Selection)에 유리해지며, 희소 모델(Sparse Model)을 생성할 수 있게 된다. 여기서 "희소(Sparse)"란, 가중치 벡터에서 대부분의 값이 0에 가까워져 일부 특성들은 모델에서 아예 사용되지 않게 되는 것을 의미한다. 결과적으로 L1 정규화를 거쳐 몇몇 중요한 가중치들만 남게 된다.
예를 들어, 데이터에 수많은 특성이 포함되어 있을 때 L1 정규화를 사용하면 덜 중요한 특성의 가중치가 0이 되어 모델을 단순화할 수 있다.
L2 정규화와 Lidge Regression
L2 정규화는 비용 함수에 L2 norm(Euclidean Distance)의 제곱을 가중치 제약으로 추가하여 과적합을 방지하는 기법이다. L2 norm은 벡터의 각 요소의 제곱합의 제곱근으로 정의된다.
$$ \|w\|_2 = \sqrt{\sum_{i=1}^{n} w_i^2} $$
예를 들어 \( w = (3, -4) \)가 있을 때 아래와 같이 계산된다.
$$ \|w\|_2 = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$
이는 벡터의 크기를 측정하는 가장 일반적인 방법으로, 벡터의 에너지를 나타낸다고도 볼 수 있다.
위 수식에서 보이는 바와 같이 L2 정규화는 가중치의 제곱합을 최소화한다. 또한 선형 회귀 모델에서 L2 규제를 주는 것을 Ridge Regression이라고 한다.
손실 함수와 비용 함수는 다음과 같이 정의된다. 손실 함수는 L1 정규화와 동일한 함수를 사용하였다.
$$ Loss(w) = \sum_{i=0}^{N} \left( y_i - \sum_{j=0}^{M} x_{ij} w_j \right)^2 $$
$$ Cost = \text{Loss}(w) + \lambda \sum_{i=1}^{n} w_i^2 $$
여기서 \( \lambda \)는 모델의 가중치를 작게 유지하여 과적합을 방지하는 역할을 한다.
역전파(Backpropagation) 과정에서 비용 함수(Cost)를 최소화하는 것 외에도, 정규화 기법을 사용하여 가중치가 지나치게 커지는 것을 방지한다. 또한, 특성 간의 중요도를 완전히 제거하지 않고도 모델이 일반화될 수 있게 돕는다. 결과적으로 가중치를 작게 유지하며, 과적합을 줄이는 데 효과적인 학습을 진행할 수 있다.
예를 들어, 다중 선형 회귀 문제에서 L2 정규화를 적용하면 모든 특성의 기여를 균등하게 줄이며 안정적인 예측을 도울 수 있다.
| 항목 | L1 정규화 | L2 정규화 |
| 정규화 항 | \( \lambda \sum_{j=0}^{M} |W_j| \) | \( \lambda \sum_{j=0}^{M} W_j^2 \) |
| 가중치의 효과 | 일부 가중치 0으로 만들어 희소성 확보 | 모든 가중치를 작게 유지 |
| 적용 결과 | 특성 선택(feature selection) | 모델 일반화 및 안정화 |
Normalization
Normalization은 입력 데이터의 크기나 분포를 일정한 범위로 조정하여 학습을 안정화시키기 위해 사용된다. 이는 주로 데이터 전처리나 모델 내부에서 수행된다. 학습 안정화는 결국 학습 속도 개선에 영향을 미치게 되며 과적합도 간접적으로 방지할 수 있게 된다. 뿐만 아니라 학습 시 출력값을 정규화하기 때문에 가중치 초기값에 대한 민감도를 줄이며 기울기 소실 문제도 일부 완화할 수 있다.
주요 특징
- Input 크기와 분포 조정
- 학습 속도 개선
- 가중치 초기값에 대한 의존성 감소
- 과적합 간접 방지
- 기울기 소실(Gradient Vanishing) 예방
여러 Normalization이 있지만 그 중 가장 대표적인 배치 정규화(Batch Normalization)에 대해 살펴보자.

배치 정규화(Batch Normalization)
배치 정규화(Batch Normalization)는 학습 과정에서 활성화 함수의 출력값을 정규화하여 학습을 가속화하고 안정화하는 방법이다. 정규화 과정은 일반적으로 미니배치 단위로 이루어진다.
$$ \hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} $$
여기서 \( \mu \)는 배치 평균, \( \sigma^2 \)는 배치 분산, \( \epsilon \)은 작은 값으로, 0으로 나누는 것을 방지한다. 이후 학습 가능한 파라미터 \( \gamma \)와 \( \beta \)를 사용하여 출력값을 조정한다.
$$ \hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} $$
기울기 소실 문제를 완화하며, 학습 속도를 향상시키며 초기화 민감도를 줄인다.
예를 들어, CNN 모델에서 배치 정규화를 활성화 함수 이전 또는 이후에 추가하여 학습 안정성을 높일 수 있다.
Regularization vs Normalization
Regularization: 모델의 복잡도를 제어하여 과적합을 방지하고 모델의 일반화 능력을 향상시키는 목적이다.
Normalization: 데이터 분포 조정을 통해 학습을 안정화시켜 모델의 빠른 수렴과 학습 과정 중 기울기 소실을 예방하는데 초점을 둔다.
관련 포스팅
참고 자료
https://amber-chaeeunk.tistory.com/69
https://esj205.oopy.io/4b321662-5d02-4559-8677-7e974cf080a8
https://hyebiness.tistory.com/11
https://arxiv.org/pdf/1803.08494

