SVM(Support Vector Machine)은 지도 학습(Supervised Learning) 알고리즘 중 하나로, 주어진 데이터가 어떤 카테고리에 속하는지를 분류하는 데 사용된다. 특히 이진 분류 문제에서 강력한 성능을 발휘하며, 고차원 공간에서도 효과적으로 작동하는 특징을 가진다.
SVM은 다양한 분야에서 활용되고 있다. 얼굴 인식, 손글씨 숫자 인식 등의 이미지 분류 문제에서 높은 성능을 보인다. 또한 스팸 메일 필터링, 감성 분석과 같은 자연어 처리 분야에서도 활용할 수 있다. 더 나아가 유전자 데이터 분석에도 활용되는데 질병 예측, 유전자 패턴 분석 등에서 사용 가능하다.
SVM이란
SVM은 데이터를 가장 잘 분리할 수 있는 결정 경계(Decision Boundary)를 찾는 것이 핵심이다. 쉽게 말해, 결정 경계를 최대한 넓게 설정하여 마진(margin)을 최대화하는 방향으로 학습을 진행한다. 여기서 마진이란, 결정 경계와 각 클래스의 가장 가까운 데이터 포인트(서포트 벡터) 사이의 거리이다. 마진이 클수록 일반화 성능이 좋아질 가능성이 높다. 이 결정 경계는 아래 그림과 같이 가중치 벡터 w와 직교하면서 margin이 최대가 되는 선형을 찾는다.

SVM의 주요 요소는 아래와 같다.
- 서포트 벡터(Support Vector): 결정 경계와 가장 가까운 데이터 포인트로, 이 점들이 결정 경계를 형성하는 데 중요한 역할을 한다.
- 마진(Margin): 결정 경계와 서포트 벡터 사이의 거리로, 이 거리를 최대화하는 것이 SVM의 목표이다.
- 커널 함수(Kernel Function): SVM은 비선형 데이터도 분류할 수 있도록 커널 함수를 사용한다. 이를 통해 저차원 데이터를 고차원 공간으로 변환하여 선형적으로 분리할 수 있도록 만든다.
위 Fig 1과 같이 단순해보이는 데이터 분포에선 결정 경계의 구간을 비교적 쉽게 예상할 수 있다. 하지만 현실 세계에선 아래와 같은 상황이 더욱 빈번하게 발생한다.
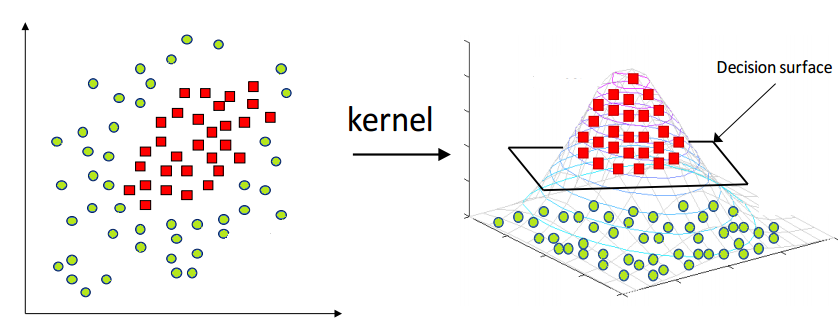
Fig 2의 왼쪽과 같은 데이터 분포가 나타난다면 2차원 평면에서 단순 선형으로 분류해 내긴 쉽지 않다. 따라서 저차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 매핑해 주는 작업을 통해 분류해 낼 수 있는데 이를 커널 트릭(Kernel Trick)이라고 한다. 이를 위한 커널 함수는 여러 종류가 있다. 아래에서 좀 더 살펴보자.
SVM의 커널 함수
SVM은 단순한 선형 분류기뿐만 아니라, 다양한 커널 함수를 활용하여 비선형 데이터를 분류하는 데에도 활용된다. 대표적인 커널 함수는 다음과 같다.

- 선형 커널(Linear Kernel): 데이터가 선형적으로 분리 가능할 때 사용한다.
- 다항식 커널(Polynomial Kernel): 다항식 형태로 데이터를 변환하여 선형적으로 분리할 수 있도록 한다.
- RBF(Radial Basis Function) 커널: 가장 많이 사용되는 커널 중 하나로, 데이터가 선형적으로 분리되지 않을 때 적합하다.
- 시그모이드(Sigmoid) 커널: 신경망에서 사용하는 활성화 함수와 유사한 형태를 가지며, 특정한 경우에 유용하다.
아래는 python과 sklearn을 사용해 구현한 소스 코드이다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# 데이터 생성
X, y = datasets.make_moons(n_samples=100, noise=0.1, random_state=42)
# 서로 다른 커널을 사용하여 SVM 모델 생성
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
models = []
for kernel in kernels:
if kernel == 'poly':
clf = svm.SVC(kernel=kernel, degree=3)
else:
clf = svm.SVC(kernel=kernel)
clf.fit(X, y)
models.append((kernel, clf))
# 시각화
fig, axes = plt.subplots(2, 2, figsize=(10, 10))
axes = axes.ravel()
for idx, (kernel, model) in enumerate(models):
ax = axes[idx]
ax.set_title(f"Kernel: {kernel}")
# 결정 경계 그리기
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, alpha=0.3)
ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.tight_layout()
plt.show()
SVM은 강력한 분류 성능을 자랑하는 알고리즘으로, 특히 이진 분류 문제에서 좋은 성능을 보인다. 또한 커널 트릭을 활용하여 비선형 데이터도 효과적으로 처리할 수 있다. 그러나 데이터 크기가 커질수록 연산량이 많아지는 단점이 있어, 적절한 데이터 전처리와 하이퍼파라미터 튜닝이 필요하다. 과적합(Overfitting) 문제도 물론 조심해야 하는 부분 중 하나이다. 머신러닝의 지도학습의 주요 방법 중 하나인 SVM의 개념과 원리를 이해하고, 실제 데이터에 적용해 보는 것이 중요하다.
참고 자료
https://www.linkedin.com/pulse/role-svm-model-current-data-science-deepak-kumar/
https://www.codeover.in/blog/introduction-to-svm-machine-learning
https://www.reneshbedre.com/blog/support-vector-machine.html

