Cross Entropy
Cross Entropy는 확률 분포 간의 차이를 측정하는 지표로, 분류 문제에서 모델의 예측 성능을 평가하는 데 자주 사용된다. 이는 손실 함수의 한 종류이며, 손실 함수의 목표는 모델이 예측한 분포와 실제 분포 사이의 차이를 최소화하는 것이다.
Cross Entropy를 이해하기 전 먼저 짚고 넘어가야 하는 개념이 있는데 바로 놀람도, 기대값, 엔트로피 이 세 가지이다.
먼저 놀람도에 대한 예를 들어보자.
검은색 종이 999개와 흰색 종이가 1개 들어있는 상자가 있다고 가정하자. 이 상자에서 우리가 검은색 종이를 뽑았다면 우리는 당연하다고 생각할 것이다. 확률(\( p(x) \))이 훨씬 높기 때문이다. 하지만 흰색 종이가 나온다면 우리는 놀라게 될 것이다. 다시 말하면 이 놀람 또는 의외성(\( \frac{1}{p(x)} \))의 정도는 확률과 반비례하는 관계이다. 정보 이론에선 이 놀람도를 정보라고 표현한다. 이 놀람도를 표현할 때는 좀 더 정보를 효율적으로 전달하기 위해 log를 사용한다.
$$ log(\frac{1}{p(x)}) = log(1)-log(p(x)) = 0 - log(p(x)) = -log(p(x)) $$
다음으로 기대값이란 만약 축구 경기에서 한 선수의 기량이 10점 만점에 8의 기량을 가지고 있다고 가정하자. 이때 이 선수가 제 기량을 발휘할 확률이 70%라면 이 선수의 기대값은 \( 8*0.7=5.6 \)이 된다. 이러한 방식으로 여러 선수가 한 팀을 이루고 그 팀의 기대값에 대해 계산해 보면 수식은 아래와 같다.
$$ E(x) = \sum{x}p(x) $$
마지막으로 엔트로피는 위 기대값의 \( x \)에 놀람도를 대입해 주면 된다.
$$ H(x) = \sum{log(\frac{1}{p(x)})}p(x) $$
Cross Entropy는 위 엔트로피 수식에서 \( log(\frac{1}{p(x)}) \)를 \( log(\frac{1}{q(x)}) \)로만 바꿔주면 된다. 출력하는 확률 분포 \( p \)와 실제 정답 분포 \( q \) 사이의 평균적인 정보 손실을 나타낸다.
크로스 엔트로피는 다음과 같이 정의된다.
$$ H(p, q) = \sum{log(\frac{1}{q(x)})}p(x) $$
$$ H(p, q) = - \sum_{i} \log(q(i)) p(i) $$
여기서 \( p(i) \)는 실제 분포에서 클래스 i에 대한 확률이며 \( q(i) \)는 모델이 예측한 클래스 \( i \)에 대한 확률이다.
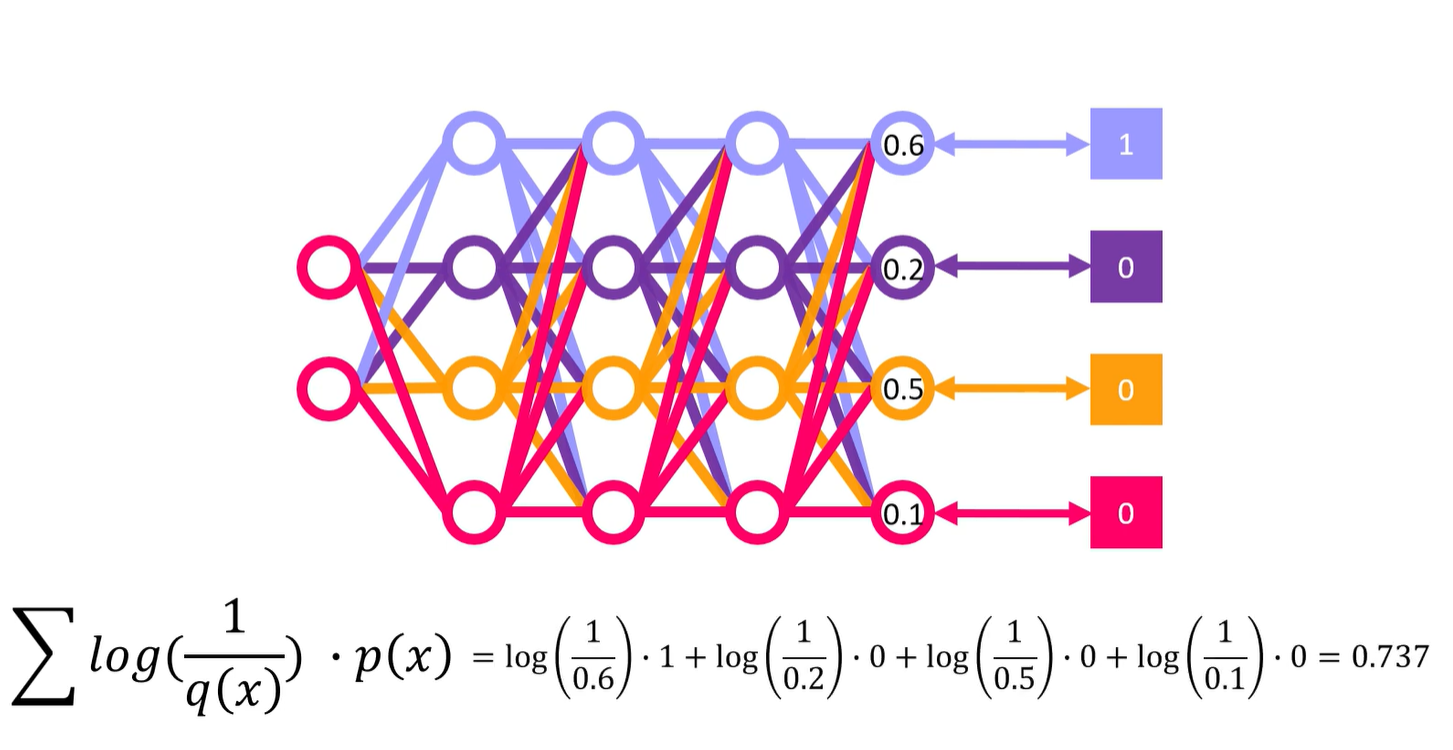
위 그림과 같이 예측 확률과 실제 값의 차이가 크면 Cross Entropy Loss의 값이 커진다. 이를 역전파를 통해 가중치 업데이트가 진행된다면 아래처럼 Loss가 작아질 것이다.
Cross Entropy vs MSE
Cross Entropy는 분류 문제에서 MSE(Mean Squared Error)보다 여러 면에서 유리하다. 특히, 확률 분포를 다루며 각 클래스에 대한 확률 예측을 하는 분류 모델에 적합한 손실 함수로, 분류 문제의 특성과 모델의 학습 효율성 측면에서 다음과 같은 장점을 가진다.
- 확률 분포와 정보 손실
: 크로스 엔트로피는 두 확률 분포 간의 차이를 정확히 측정하며, 모델이 정답 클래스의 확률을 최대화하도록 유도한다. MSE는 연속적인 회귀에 적합해 분류 문제에서 확률 분포 차이를 정확히 반영하지 못할 수 있다. - 경사 소실 문제 감소
: MSE를 사용하면 예측이 정답에 가까워질수록 경사가 작아져 학습이 느려질 수 있다. 반면, 크로스 엔트로피는 학습 초반에도 더 큰 기울기를 제공해 빠르게 수렴한다. - 명확한 분류 능력
: 크로스 엔트로피는 정답 클래스에 높은 확률, 오답 클래스에 낮은 확률을 할당하는 방향으로 학습해, 분류 경계를 명확히 한다. MSE는 확률이 평균으로 수렴하는 경향을 유발할 수 있다. - 클래스 불균형에 유연
: 크로스 엔트로피는 소수 클래스의 예측 오류에도 민감하게 반응하므로, 클래스가 불균형한 상황에서 더 효과적이다. MSE는 모든 클래스의 예측 오류를 균등하게 반영해, 소수 클래스 오류를 간과할 수 있다.
Cross Entropy와 Softmax
Cross Entropy와 Softmax는 분류 문제에서 자주 결합하여 사용된다. 특히 이 조합은 역전파(Backpropagation)를 통해 기울기(Gradient)를 계산할 때 편미분이 간단히 정리되어 계산이 용이하다는 장점이 있다.
우선 Softmax는 각 클래스에 대한 확률을 계산하는 함수로, 주어진 입력 벡터 \( z = (z_1, z_2, ..., z_k) \)에 대해 각 클래스 \( i \)의 확률 \( P(y = i|z) \)는 다음과 같이 정의된다.
$$ P(y = i | z) = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}} $$
여기서 \( z_i \)는 클래스 \( i \)에 해당하는 예측 값이며, \( k \)는 클래스의 수다.
Cross Entropy Loss는 실제 정답 분포 \( P \)와 예측된 확률 분포 \( Q \) 간의 차이를 측정하는 함수로, \( N \)개의 샘플에 대해 다음과 같이 정의된다.
$$ L = - \sum_{i=1}^{N} \sum_{c=1}^{k} p_{i,c} \log(q_{i,c}) $$
여기서, \( p_i \), \( c \)는 샘플 \( i \)에 대해 실제 정답이 클래스 \( c \)일 확률(One-hot Vector에서 1 또는 0), \( q_i \), \( c \)는 예측된 클래스 \( c \)에 대한 확률이다.
이제 이 조합의 역전파 과정 속 미분 과정을 계산해 보자.
우선 Softmax의 출력은 확률로 해석되며, 이 확률의 변화에 대한 편미분은 다음과 같다.
$$ \frac{\partial P(y=i|z)}{\partial z_j} = P(y=i|z) \left( \delta_{ij} - P(y=j|z) \right) $$
여기서 \( \delta_{ij} \)는 \( i = j \)일 때 1, 그렇지 않으면 0이다. 이 미분 결과는 소프트맥스 함수의 출력 간의 상호작용을 반영한다.
Cross Entropy Loss는 예측 확률과 실제 정답 확률 간의 차이를 측정하므로, 예측 확률 \( p_i \), \( c \)에 대한 미분을 구할 수 있다. 이때 중요한 점은 Cross Entropy와 Softmax가 결합되어 계산이 단순화된다는 것이다. 이를 계산하면 다음과 같다.
$$ \frac{\partial L}{\partial z_j} = P(y=j|z) - q_j $$
여기서, \( q_i \)는 실제 클래스에 대한 One-hot 벡터 값이다. 이 식을 통해 알 수 있는 점은, 역전파에서의 미분값이 단순히 예측 확률에서 실제 레이블 확률을 뺀 값으로 계산된다는 것이다. 이는 계산이 매우 간단하고 효율적이다.
이제 전체 계산 과정을 살펴보자. Cross Entropy와 Softmax를 결합한 후 역전파 계산은 다음과 같은 형태로 전개된다.
우선 위에서 확인한 것처럼 소프트맥스 함수의 출력 P에 대해 다음과 같이 전개된다.
$$ P(y = i | z) = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}} $$
마지막으로 Cross Entropy Loss의 미분은 다음과 같다.
$$ \frac{\partial L}{\partial z_j} = P(y=j|z) - q_j $$
이렇게 간단하게 정리가 가능하다. 모델의 파라미터 업데이트 시에는 이 미분값을 사용하여 가중치를 업데이트하게 된다. 그러므로 위와 같이 Cross Entropy Loss와 Softmax를 함께 사용하게 되면 역전파 과정에 대해 계산 효율성을 증가시킬 수 있다.
관련 포스팅
2024.10.27 - [Data Science/ML & DL] - Softmax에 대한 고찰
참고 자료
https://www.youtube.com/watch?v=vAaReyHMfY8&t=170s
https://www.youtube.com/watch?v=KJJL9_mlMXA
