Sort(정렬) 알고리즘 정리

자주 사용하는 정렬 알고리즘들을 정리해보려 한다.

 

버블 정렬(Bubble Sort)

• 정의: 인접한 원소들을 비교하여 큰 값을 뒤로 보내는 정렬
• 시간복잡도: O(n²) - 삽입/삭제 후 재정렬 필요, 검색 O(n)

Fig 1. Bubble Sort

 

의사코드

for i = 0 to n-2:
    for j = 0 to n-2-i:
        if arr[j] > arr[j+1]:
            swap(arr[j], arr[j+1])

 

선택 정렬(Selection Sort)

• 정의: 최솟값을 찾아 앞쪽부터 차례로 배치하는 정렬
• 시간복잡도: O(n²) - 삽입/삭제 후 재정렬 필요, 검색 O(n)

Fig 2. Selection Sort

의사코드

for i = 0 to n-2:
    min_idx = i
    for j = i+1 to n-1:
        if arr[j] < arr[min_idx]:
            min_idx = j
    swap(arr[i], arr[min_idx])

 

삽입 정렬(Insertion Sort)

• 정의: 각 원소를 정렬된 부분의 적절한 위치에 삽입하는 정렬
• 시간복잡도: O(n²) - 삽입 O(n), 삭제 O(n), 검색 O(n)

Fig 3. Insertion Sort

 

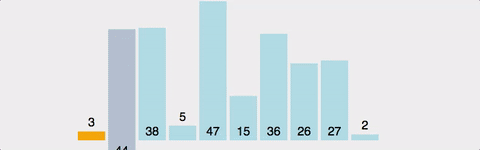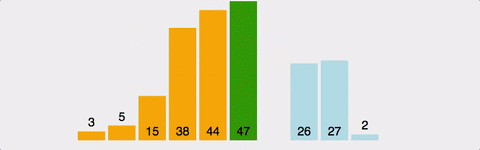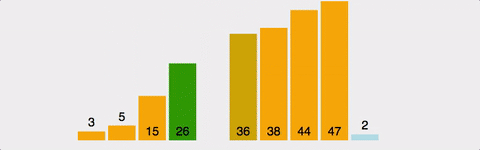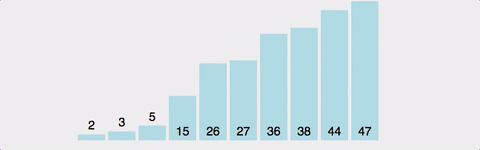
의사코드

for i = 1 to n-1:
    key = arr[i]
    j = i-1
    while j >= 0 and arr[j] > key:
        arr[j+1] = arr[j]
        j = j-1
    arr[j+1] = key

 

병합 정렬(Merge Sort)

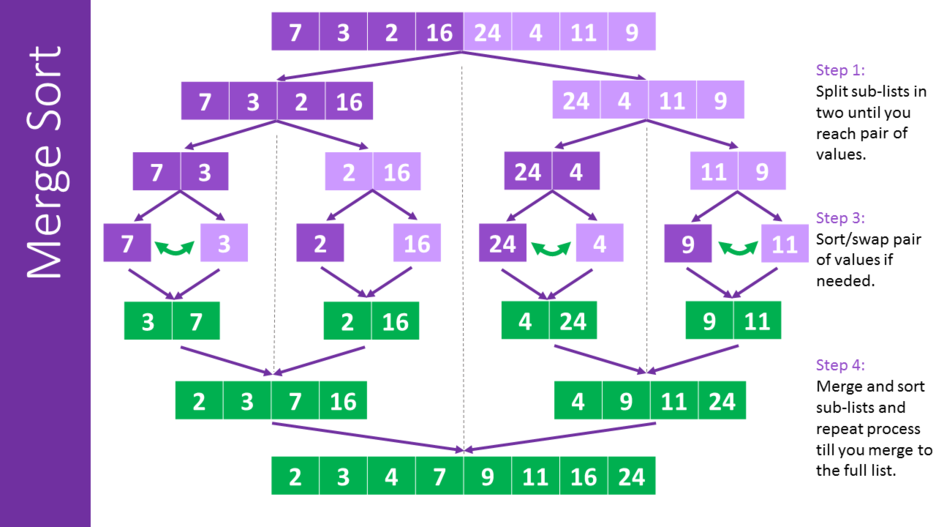
• 정의: 분할 정복으로 배열을 나누고 병합하며 정렬
• 시간복잡도: O(n log n) - 삽입/삭제 후 재정렬 필요, 검색 O(n)

Fig 4. Merge Sort

 

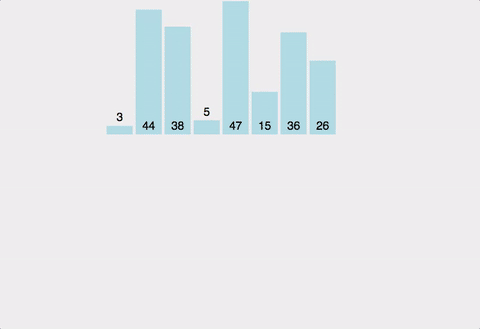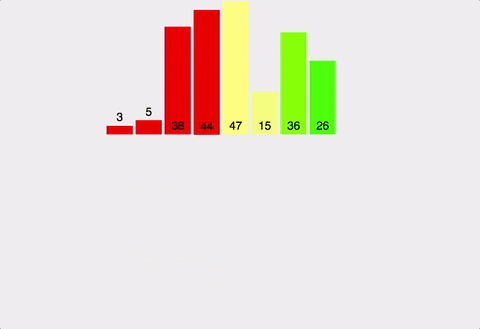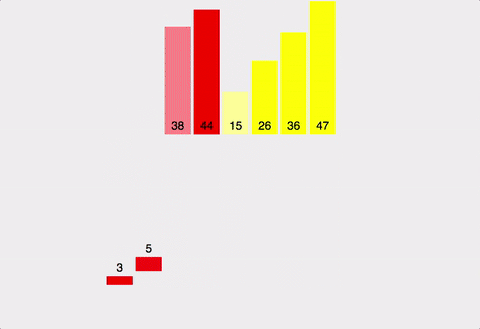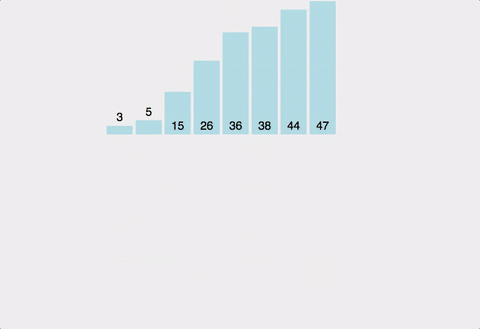
의사코드

mergeSort(arr, left, right):
    if left < right:
        mid = (left + right) / 2
        mergeSort(arr, left, mid)
        mergeSort(arr, mid+1, right)
        merge(arr, left, mid, right)

 

퀵 정렬(Quick Sort) - 분할 정복

• 정의: 피벗을 기준으로 분할하여 정렬하는 분할 정복 알고리즘
• 시간복잡도: 평균 O(n log n), 최악 O(n²) - 삽입/삭제 후 재정렬 필요, 검색 O(n)

Fig 5. Quick Sort

 

의사코드

quickSort(arr, low, high):
    if low < high:
        pi = partition(arr, low, high)
        quickSort(arr, low, pi-1)
        quickSort(arr, pi+1, high)

partition(arr, low, high):
    pivot = arr[high]
    i = low-1
    for j = low to high-1:
        if arr[j] <= pivot:
            i++
            swap(arr[i], arr[j])
    swap(arr[i+1], arr[high])
    return i+1

 

Quick Sort는 위의 시간복잡도를 자세히 보면 성능의 이중성이 있는 것을 알 수 있다.

• 평균: O(n log n) - 매우 빠름
• 최악: O(n²) - 매우 느림

이는 피벗 선택에 따라 성능이 극단적으로 달라지기 때문이다.

 

퀵 정렬은 줄 세우기 게임으로 설명이 비유할 수 있다. 예를 들어 한 명을 기준(피벗)으로 세워두고, 나머지를 "기준보다 작은 사람은 왼쪽, 큰 사람은 오른쪽"으로 나눈다고 가정하자.

data: [7, 2, 9, 1, 5]
기준을 7로 정함

7보다 작은 항목: [2, 1, 5]
7과 동일한 항목: [7]
7 보다 큰 항목: [9]

 

case 1. 운이 좋을 때(기준을 잘 골랐을 때)

[5, 1, 9, 2, 8] → 기준 5
[1, 2] [5] [9, 8] → 반반 나눠짐 → 빠름

 

case 2. 운이 나쁠 때(기준을 잘못 골랐을 때)

[1, 2, 3, 4, 5] → 기준 5
[1, 2, 3, 4] [5] [] → 한쪽만 많음 → 느림

 

다시 말해 Quick Sort는 기준 하나 정해서 양쪽으로 나누는 정렬인데, 기준을 잘 고르면 엄청 빠르고 못 고르면 엄청 느린 도박성 정렬이라고 볼 수 있다. 하지만 실제로 대부분의 라이브러리에서 기본 정렬로 채택하고 있는데 이는 평균 성능이 뛰어나고, 개선 기법들로 최악 케이스 회피 가능하기 때문이다. 개선 기법들은 대표적으로 다음과 같은 방법들이 있다.

• Randomized Pivot: 피벗을 랜덤 선택
• 3-way Partitioning: 중복값 처리 최적화
• Hybrid Sort: 작은 배열에서는 삽입정렬 사용

 

한 가지 더 의문이 생긴다. Quick Sort의 정렬에 대한 시간 복잡도는 Merge Sort의 최악의 경우와 동일한데도 많이 사용하는 이유가 무엇일까? 이유는 다음과 같다.

 

Merge Sort는 원본 배열 + 추가 배열 = 2배의 메모리 필요한데 비해, Quick Sort는 원본 배열 = 1배만큼의 메모리만 있어도 된다. 이러한 특성은 큰 데이터에서는 메모리가 부족할 수 있거나 서버 환경에서 메모리 비용이 중요한 환경에서 이점을 가져가기 때문이다.

 

힙 정렬(Heap Sort)

• 정의: 힙 자료구조를 이용한 정렬 알고리즘
• 시간복잡도: O(n log n) - 삽입/삭제 O(log n), 검색 O(n)

Fig 6. Heap Sort

 

의사코드

heapSort(arr):
    buildMaxHeap(arr)
    for i = n-1 to 1:
        swap(arr[0], arr[i])
        heapify(arr, 0, i)

buildMaxHeap(arr):
    for i = n/2-1 to 0:
        heapify(arr, i, n)

 

---

 

참고 자료

 

https://hyo-ue4study.tistory.com/68

 

https://emre.me/algorithms/sorting-algorithms/#heap-sort