신호처리를 처음 접했던 이후 언젠가 푸리에 변환에 대한 제대로 된 이해와 정리가 필요하다 느꼈다. 푸리에 변환에 대해 공부하기 전 사전 지식으로 푸리에 급수(Fourier Series)와 푸리에 계수(Fourier Coefficient)에 대해 먼저 정리하려 한다.
푸리에 급수와 푸리에 계수에 대한 설명 이전에 이해를 돕기 위해 Sinusoids(정현파)와 Periodic Waveforms(주기 신호)에 대해서 간단히 설명하려 한다.
우선 Sinusoids이다. 이는 시간에 따라 변하는 신호를 설명하는 기본적인 수학적 표현이다. 즉, 코사인파(cosine wave) 또는 사인파(sine wave)를 수식으로 나타낸 것이다.
$$ x(t) = A \cos(2\pi f t + \phi) = A \cos(\omega t + \phi) $$
- 𝐴 : amplitude
- 𝑓 : cycle frequency or just frequency (Hz)
- 𝜙 : phase-shift
- 1/𝑓 : period (length of one cycle in time, 𝑇)
- 𝜔 : radian frequency (rad/sec)
- 𝜔/2𝜋 : cycle frequency or just frequency (= 𝑓)
- 2𝜋/𝜔 : period (length of one cycle in time, 𝑇)
Periodic Waveforms는 sinusoids의 합으로써 합성할 수 있다.
$$ x(t) = A_0 + \sum_{k=1}^{\infty} A_k \cos \left( 2\pi k f_0 t + \phi_k \right) $$
- \( f_0 \): fundamental frequency
- \( kf_0 \) : harmonic of \( f_0 \)(harmonic frequency)
- \( 1/f_0 \) : fundamental period (\( T_0 \))
- 𝜙𝑘 : phase-shift
여기서 Fundamental Frequency는 현재 합성된 periodic waveforms에서 가장 낮은 주파수이다. harmonic은 우리말로 고조파라 부르는데 이는 \( f_0 \)의 정수배(k)로 표현된다. \( f_0 \)는 신호 전체가 정확히 반복되는 최소 단위로 사용되기 때문에 Fundamental이 된다.
참고로 \( A_0 \)는 DC값 또는 평균 진폭을 표현하는데 만약 0이 아니라면 좌표평면상 어딘가로 치우쳐있다는 말이 된다.
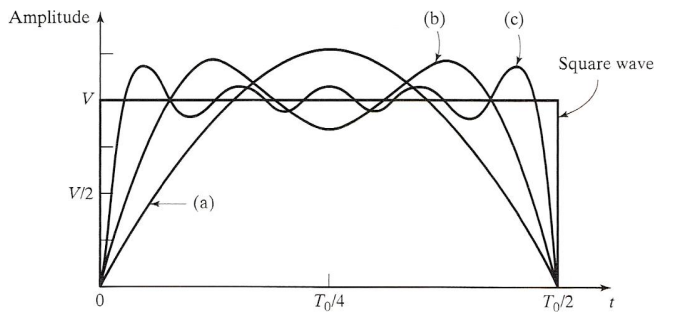
이렇게 \( f_0 \)와 고조파의 조합으로 복잡한 주기파형을 만들어낼 수 있고 이는 푸리에 급수(Fourier Series)로 표현할 수 있다.
푸리에 급수(Fourier Series)
푸리에 급수(Fourier Series)는 sin파와 cos파를 이용하여 모든 주기 함수에 대해 표현할 수 있을까라는 물음에서 시작되었다. 즉, 세상에 존재하는 주기 함수를 삼각함수의 합으로 표현하는 방법이다. 이 푸리에 급수는 신호 처리, 진동 해석, 이미지 압축 등 다양한 분야에서 필수적인 역할을 한다.
위의 주기파형 수식을 그대로 가지고 온다.
$$ x(t) = A_0 + \sum_{k=1}^{\infty} A_k \cos \left( k w_0 t + \phi_k \right) $$
코사인 덧셈 공식을 이용하여 아래와 같이 변환할 수 있다.
$$ x(t) = A_0 + \sum_{k=1}^{\infty} (A_k \cos \phi_k \cos(k \omega_0 t) - A_k \sin \phi_k \sin(k \omega_0 t)) $$
\( A_0 \)는 \( a_0 \)로 치환하고, \( A_k \cos \phi_k \)는 \( a_k \), \( A_k \sin \phi_k \)는 \( -b_k \)로 치환하면 다음과 같이 표기할 수 있다.
$$ x(t) = a_0 + \sum_{k=1}^{\infty} (a_k \cos(k \omega_0 t) + b_k \sin(k \omega_0 t)) $$
만약 어떤 함수 \( f(x) \)가 주기 \( 2\pi \)를 가진다면, 다음과 같이 표기할 수 있다. \( w_0 = \frac{2\pi}{T} = \frac{2\pi}{2\pi} = 1 \)이고, 따라서 \( kw_0t \)가 그냥 \( kx \)가 된다. 좀 더 직관적으로 보기 위해 관례적으로 \( k \)는 \( n \)으로 바꾸어 표현하였다.
$$ f(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos(nx) + b_n \sin(nx) \right) $$
여기서 \( a_0, a_n, b_n \)는 다음에 설명할 푸리에 계수이다.
푸리에 계수(Fourier Coefficient)
푸리에 계수(Fourier Coefficient)는 각각 cos과 sin이 주어진 신호에서 각각 얼마나 기여하는지 수치화한 것이다.
$$ a_0 = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) \, dx $$
$$ a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(nx) \, dx $$
$$ b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(nx) \, dx $$
\( a_n \)은 코사인 계수에 해당하고, \( b_n \)은 사인 계수에 해당한다.
푸리에 계수에 대한 수식 증명은 다음과 같다.
우선 푸리에 급수 양변에 \( \cos(mx) \)를 곱하고 \( [-\pi, \pi] \) 구간에서 적분한다.
$$ \int_{-\pi}^{\pi} f(x) \cos(mx) \, dx = \int_{-\pi}^{\pi} \left( a_0 + \sum_{n=1}^{\infty} (a_n \cos(nx) + b_n \sin(nx)) \right) \cos(mx) \, dx $$
그 후 정규 직교성(orthonormal)을 이용하여 다음이 성립한다.
$$ \int_{-\pi}^{\pi} \cos(nx) \cos(mx) \, dx = \begin{cases}
\pi & \text{if } n = m \\
0 & \text{if } n \neq m
\end{cases} $$
$$ \int_{-\pi}^{\pi} \sin(nx) \cos(mx) \, dx = 0 $$
따라서 \( a_m \)만 남게 되어 다음과 같고,
$$ \pi a_m = \int_{-\pi}^{\pi} f(x) \cos(mx) \, dx $$
결과적 다음이 성립하게 된다.
$$ a_m = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(mx) \, dx $$
동일한 방법으로 \( b_n \)에 대해서도 증명할 수 있다.
푸리에 계수(Fourier Coefficient) 예제
예제로 사각파(Rectangular Wave)의 푸리에 급수 전개를 풀어보자. 여기서 사각파(Rectangular Wave)는 다음과 같은 주기 함수이다. 그림은 Fig 1을 참조하면 된다.
- 주기: \( 2\pi \)
- 구간별 정의: \( f(x) = \begin{cases}
1, & 0 < x < \pi \\
-1, & -\pi < x < 0
\end{cases} \)
이는 홀함수이므로, 코사인 항(\( a_n \))은 모두 0이다. 사인 항(\( b_n \))만 존재한다. 푸리에 계수 \( b_n \)은 다음과 같이 계산한다.
$$ b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(nx) \, dx $$
함수 \( f(x) \)의 정의를 이용하여 적분을 두 구간으로 나누면 다음과 같다.
$$ b_n = \frac{1}{\pi} \left( \int_{0}^{\pi} (1) \sin(nx) \, dx + \int_{-\pi}^{0} (-1) \sin(nx) \, dx \right) $$
$$ b_n = \frac{2}{\pi} \int_{0}^{\pi} \sin(nx) \, dx $$
이를 적분하면 다음과 같다.
$$ b_n = \frac{2}{\pi} \left( \frac{1 - (-1)^n}{n} \right) $$
따라서 \( n \)이 홀수일 때 \( b_n = \frac{4}{n\pi} \)이고, \( n \)이 짝수면 \( b_n = 0 \)이다.
결론적으로, 사각파의 푸리에 급수 전개는 다음과 같다.
$$ f(x) = \frac{4}{\pi} \left( \sin(x) + \frac{1}{3} \sin(3x) + \frac{1}{5} \sin(5x) + \frac{1}{7} \sin(7x) + \cdots \right) $$
요약하면, 사각파는 홀수 고조파 성분만 가지며, 각 고조파의 진폭은 주파수에 반비례한다. 다만 고조파를 무한히 추가하지 않으면 완벽하게 직각 모양은 나오지 않고 "깁스 현상(Gibbs phenomenon)"이라는 오버슈트가 생긴다.

