순전파 (Forward Propagation)
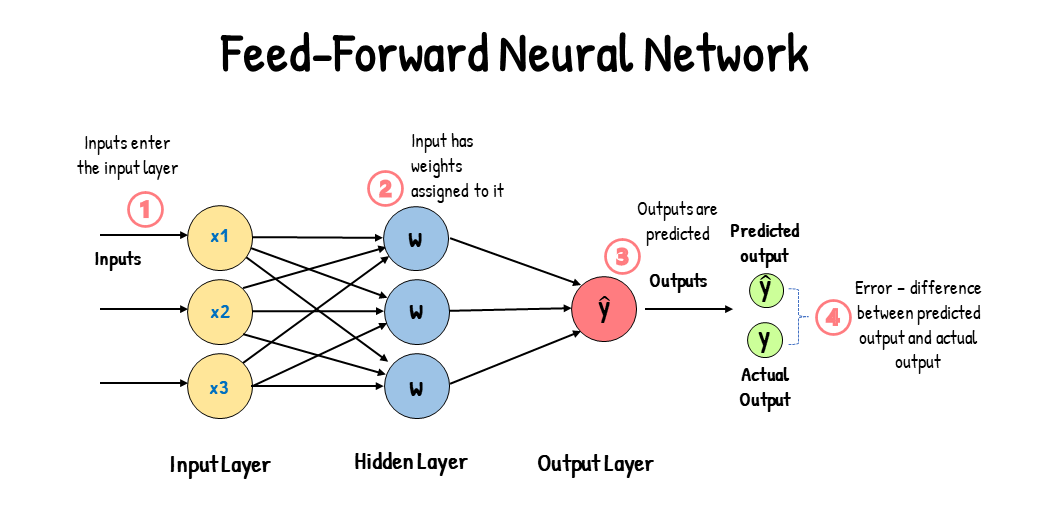
순전파(Forward Propagation)란 입력 데이터가 신경망을 통과하면서 각 층의 가중치와 편향을 통해 연산되어 최종 출력에 도달하는 과정을 의미한다. 순전파의 목표는 주어진 입력에 따라 모델이 예측 값을 계산하는 것이다.
기본적인 수식은 아래와 같다.
$$ z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)} $$
- \(z^{(l)}\): \(l\)번째 층의 선형 결합 결과
- \(W^{(l)}\): \(l\)번째 층의 가중치 행렬
- \(a^{(l-1)}\): 이전 층의 활성화 값
- \(b^{(l)}\): \(l\)번째 층의 편향 벡터
활성화 함수 \( \sigma \)를 적용하여 다음과 같이 출력 활성화 값을 얻을 수 있다.
$$ a^{(l)} = \sigma(z^{(l)}) $$
한가지 간단한 순전파 과정을 예를 들어보자.

1. 입력 및 가중치 정의
- Input: $$ x \in \mathbb{R}^d $$
- Hidden Layer의 가중치: $$ W^{(1)} \in \mathbb{R}^{h \times d} $$
2. 중간 변수 계산
- 중간 변수 \(z\): $$ z = W^{(1)} x $$
3. 활성화 함수 적용
- 숨겨진 활성화 벡터 \( h \): $$ h = \phi(z) $$
4. 출력 계산
- 출력 벡터 \(o\) (다음 층 가중치 \(W^{(2)}\) 사용): $$ o = W^{(2)} h $$
5. 손실 함수 정의
- 데이터에 대한 손실 항 \(L\): $$ L = l(o, y) $$
6. 정규화 항 정의
- 정규화 항 \(s\): $$ s = \frac{\lambda}{2} (\|W^{(1)}\|_F^2 + \|W^{(2)}\|_F^2) $$
7. 모델의 정규화된 손실
- 최종 손실 \(J\): $$ J = L + s $$
순전파 과정에서 발생하는 오차를 수정하지 않으면 가중치 조정이 불가능하다. 이를 해결하기 위해 역전파가 필요하다.
오차 역전파 (Backpropagation)

오차 역전파(Backpropagation)란 모델의 출력과 실제 값 사이의 오차를 이용해 각 가중치에 대한 기울기를 계산하고, 이를 통해 가중치를 조정하는 과정이다. 역전파는 순전파와 반대 방향으로 진행되며, 오류가 모델의 출력부터 입력 방향으로 전파되어 각 층의 가중치가 업데이트된다.
손실 함수 \( L \)에 대해 최종 출력 \( a^{(L)} \)의 가중치 기울기를 계산하려면, 다음과 같이 연쇄 법칙(Chain Rule)을 적용한다. 한가지 예시를 통해 계산해보자.

1. 목표의 기울기 계산
- 손실 항에 대한 기울기: $$ \frac{\partial J}{\partial L} = 1 $$
- 정규화 항에 대한 기울기: $$ \frac{\partial J}{\partial s} = 1 $$
2. 출력 층의 기울기 계산
- 출력 \(o\)에 대한 기울기: $$ \frac{\partial J}{\partial o} = \text{prod}\left(\frac{\partial J}{\partial L}, \frac{\partial L}{\partial o}\right) = \frac{\partial L}{\partial o} \in \mathbb{R}^q $$
3. 가중치에 대한 기울기 계산
- 정규화 항 \(s\)에 대한 가중치 기울기:
$$ \frac{\partial s}{\partial W^{(1)}} = \lambda W^{(1)} $$ $$ \frac{\partial s}{\partial W^{(2)}} = \lambda W^{(2)} $$
4. 가중치 업데이트를 위한 기울기
- 가중치 \(W^{(2)}\)에 대한 기울기: $$ \frac{\partial J}{\partial W^{(2)}} = \text{prod}\left(\frac{\partial J}{\partial o}, \frac{\partial o}{\partial W^{(2)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial W^{(2)}}\right) = \frac{\partial J}{\partial o} h^T + \lambda W^{(2)} $$
5. Hidden Layer로 기울기 전파
- 숨겨진 활성화 \(h\)에 대한 기울기: $$ \frac{\partial J}{\partial h} = \text{prod}\left(\frac{\partial J}{\partial o}, \frac{\partial o}{\partial h}\right) = W^{(2)T} \frac{\partial J}{\partial o} $$
6. 활성화 함수에 대한 기울기
- 중간 변수 \(z\)에 대한 기울기: $$ \frac{\partial J}{\partial z} = \text{prod}\left(\frac{\partial J}{\partial h}, \frac{\partial h}{\partial z}\right) = \frac{\partial J}{\partial h} \odot \phi'(z) $$
7. 가중치 \(W^{(1)}\)에 대한 기울기
- 가중치 \(W^{(1)}\)에 대한 기울기: $$ \frac{\partial J}{\partial W^{(1)}} = \text{prod}\left(\frac{\partial J}{\partial z}, \frac{\partial z}{\partial W^{(1)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial W^{(1)}}\right) = \frac{\partial J}{\partial z} x^T + \lambda W^{(1)} $$
8. 최종
- 연쇄 법칙에 따라 완성된 최종적인 표현: $$ \frac{\partial J}{\partial W^{(1)}} = \left( \left( W^{(2)^T} \frac{\partial L}{\partial o} \right) \odot \varphi'(W^{(1)} x) \right) x^T + \lambda W^{(1)} $$
깊은 네트워크의 경우 기울기 소실(Gradient Vanishing) 문제가 발생해 학습이 어렵다. 기울기가 0에 가까워지면서 가중치가 효과적으로 업데이트되지 않는 상황이 발생할 수 있기 때문이다.
이는 ReLU와 같은 비선형 활성화 함수를 사용하거나, 잔차 연결(Residual Connection)을 통해 기울기 소실을 완화할 수 있다. 또한 Batch Normalization을 통해 신경망의 내부 활성화 분포를 정규화하여 안정적인 학습을 유도할 수 있다.
기울기 소실뿐만 아니라 기울기 폭주(Gradient Exploding)도 존재하는데 이는 기울기가 너무 커져 가중치가 발산하는 문제이다.
이는 Gradient Clipping으로 기울기의 최대값을 제한하거나, L2 정규화를 통해 과도한 가중치 증가를 방지할 수 있다.
마지막으로 계산 비용 및 효율성에 대한 문제가 있다. 역전파는 기울기 계산을 위해 많은 연산을 필요로 하므로 학습 비용이 증가한다.
이는 Mini-Batch Gradient Descent를 사용하여 연산량을 줄이거나, GPU와 같은 병렬처리 하드웨어를 활용할 수 있다.
연쇄 법칙(Chain Rule)
역전파를 통해 가중치와 편향을 갱신할 때 발생하는 복잡한 계산은 이 연쇄 법칙을 사용하므로 비교적 간단하게 계산이 가능해진다. 연쇄 법칙(Chain Rule)이란 복합 함수의 미분을 구할 때 사용되는 방법으로, 여러 함수를 연속해서 적용할 때 각 함수의 미분을 곱해 최종 미분을 얻는 것이다. 역전파 과정에서 연쇄 법칙을 적용하면, 출력에서부터 각 층을 거슬러 올라가며 기울기를 구할 수 있다.
만약 \(y = f(g(x))\)로 표현되는 복합 함수가 있을 때, \(y\)를 \(x\)에 대해 미분한다면 수식은 아래와 같이 전개된다.
$$ \frac{dy}{dx} = \frac{dy}{dg} \cdot \frac{dg}{dx} $$
다층 신경망에서는 이러한 연쇄 법칙이 반복 적용된다. 예를 들어, 신경망에서의 최종 출력이 여러 층을 거친 함수라면 아래와 같다.
$$ y = f^{(L)}(f^{(L-1)}(...f^{(1)}(x)...)) $$
여기서 최종 출력 \(y\)의 \(x\)에 대한 기울기를 구하기 위해 각 층의 기울기를 연쇄적으로 곱해준다.
역전파 과정에서 연쇄 법칙을 사용하여 각 층의 가중치와 편향에 대한 기울기를 계산한다. 이때, 손실 함수 \(L\)를 최종 출력 값 \(a^{(L)}\)에 대해 미분한 후, 각 층의 입력 값과 가중치에 대해 차례로 미분을 수행한다.
예를 들어, \(L\)에 대해 \(l\)번째 층의 가중치 \(W^{(l)}\)에 대한 기울기는 다음과 같은 연쇄 법칙으로 구해진다.
$$ \frac{\partial L}{\partial W^{(l)}} = \frac{\partial L}{\partial a^{(L)}} \cdot \frac{\partial a^{(L)}}{\partial z^{(L)}} \cdot ... \cdot \frac{\partial a^{(l+1)}}{\partial z^{(l+1)}} \cdot \frac{\partial z^{(l)}}{\partial W^{(l)}} $$
- \(\frac{\partial L}{\partial a^{(L)}}\): 최종 출력 \(a^{(L)}\)에 대한 손실 함수의 기울기
- \(\frac{\partial a^{(L)}}{\partial z^{(L)}}\): 활성화 함수의 미분값
- \(\frac{\partial z^{(l)}}{\partial W^{(l)}}\): \(l\)번째 층의 선형 결합에 대한 가중치의 기울기
연쇄 법칙 덕분에 역전파를 통해 최종 출력층의 손실 함수로부터 시작하여 각 층별로 필요한 기울기를 전달하고, 최종적으로 모든 가중치와 편향에 대한 기울기를 구할 수 있다. 이 과정을 통해 모델의 모든 가중치가 오차를 줄이는 방향으로 조정된다.
관련 포스팅
2024.10.26 - [Data Science/ML & DL] - 손실 함수(Loss Function)와 모델 유형 및 분야 별 적용 방법
2024.10.28 - [Data Science/ML & DL] - 옵티마이저(Optimizer)와 학습률(Learning Rate)
참고 자료
https://www.youtube.com/watch?v=DMCJ_GjBXwc

